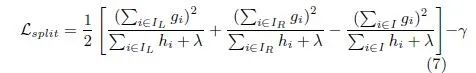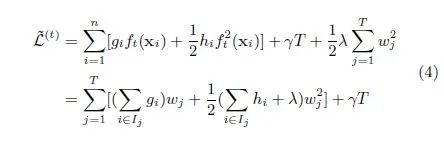GBDT与XGBOOST串讲

嘿，记得给“机器学习与推荐算法”添加星标

---

最近，一直被GBDT和XGBOOST烦恼，产生了如下的问题，由此产生了这篇文章。

• XGBOOST怎么生成一棵树？

• GBDT算法是什么？

• GBDT与BT(提升树)是一回事吗？

本篇文章结构:

Boosting Tree(提升树)

提升树是采用加法模型与前向分布算法进行提升的，是基于残差进行训练的。提升树分为回归树和二叉分类树，对于分类问题就是分类树(可以参考AdaBoost算法),对于回归问题就是回归树。至于为什么叫“提升”树？我的理解是因为是加法模型，相加进而为提升。

具体算法如下:

其中2.a步是计算残差，2.b步通过把2.a的残差当作标签,可以使用线性回归的方法进行拟合残差。通过M次循环一共得到M+1颗树，每个输入数据X的结果，是M+1棵树预测的结果之和。

GB算法

当提升树的损失函数是平方损失和指数损失时，每一步优化很简单；但是对于一般函数，优化不是非常简单，因此采用梯度下降法进行优化。至于为什么是“梯度提升”，我的理解是首先基于当前模型损失函数的负梯度信息进行拟合形成新的弱分类器,然后根据残差进行寻找该新分类器的权重!由此，即为梯度提升!

具体算法如下:

第4步，使用梯度作为标签进行拟合新的一棵树；第5步是基于残差进行得到新的一颗树的权重，其中残差来自于第i个数据的标签y与前m-1棵树的差得到的。其中F(x)表示前几棵树的总的函数。

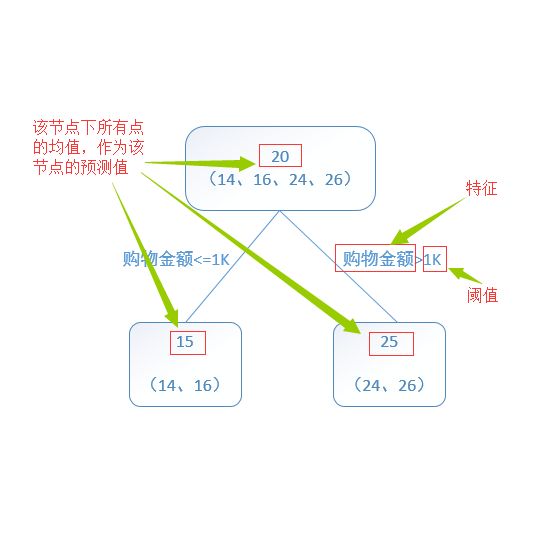
GBDT算法

有了上面的GB算法介绍，那么使用决策树作为弱分类器的GB算法被称为GBDT(Gradient Boosting Decision Tree)。一般采用CART得到决策树，CART是采用基尼指数作为决策树的损失增益函数。基尼指数反应了数据集D中任意两个样本不一致的概率。其基尼指数越高则数据集D的纯度越高；纯度越高正是决策树每个叶子节点的类别越一致。信息熵和基尼指数都是《信息论》中的内容。

XGBOOST

XGBOOST是GBDT算法的工程实现，XGBOOST的公式推导采用二阶泰勒公式的展开形式进行推导，使得每棵树之间得变化更小，而且还使用了正则化项，控制了每棵树的复杂度,进而防止过拟合。

公式推导也可以参见论文XGBoost: A Scalable Tree Boosting System

XGBOOST在生成一颗树的时候，使用如下公式进行左右分支。

训练得到第M棵树的损失函数：   

其实XGBOOST每一次分支采用的是贪心算法，对于决策说来说每次分支也是采用贪心算法，只不过每次进行分支使用的损失函数不一样。对于决策树有基尼指数、信息熵等loss函数。

参考文献:

[1]. 《统计学习方法》(提升树)

[2].《百面机器学习》(集成学习)

[3].XGBoost: A Scalable Tree Boosting System

[4].《机器学习》.西瓜书.周志华

喜欢的话点个在看吧👇