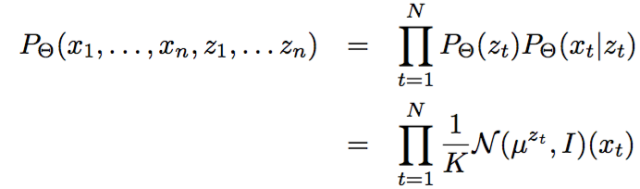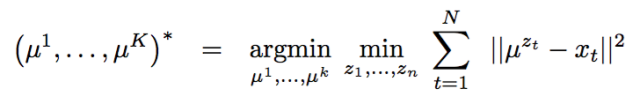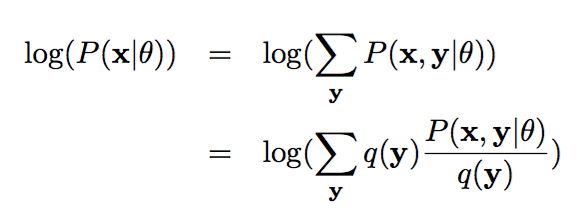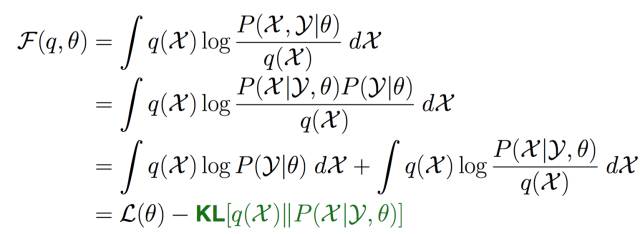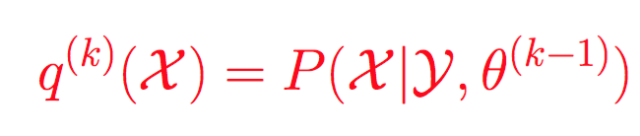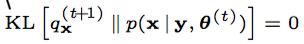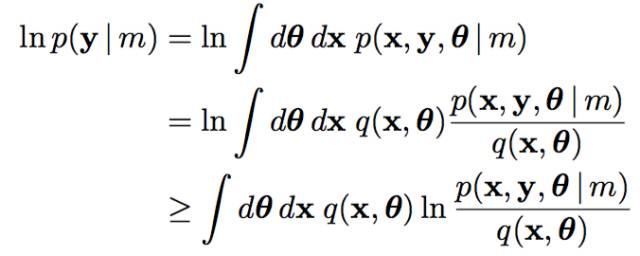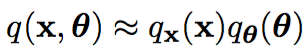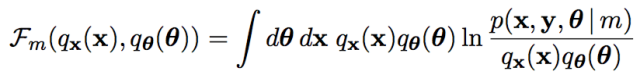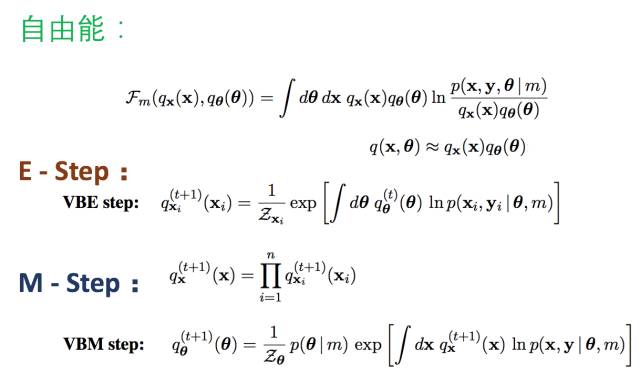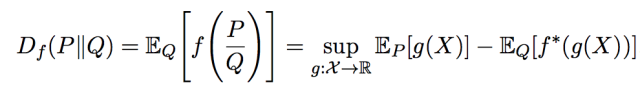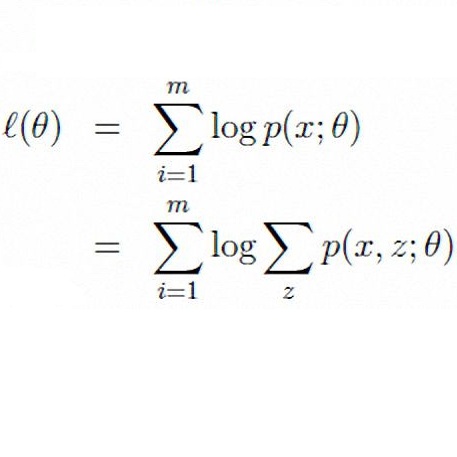EM算法的九层境界：​Hinton和Jordan理解的EM算法

导读

知乎上有一个讨论：EM算法存在的意义是什么？是什么原因使得EM算法这么流行呢？EM算法是Hinton和Jordan强强发力的领域，本文作者纵向解析EM算法的9层境界，深入浅出，值得一读。

Hinton, 这个深度学习的缔造者( 参考 攒说 Geoff Hinton ) ， Jordan 当世概率图模型的集大成者（参考 “乔丹上海行”）， 他们碰撞的领域，EM算法！这个是PCA外的，另外一个无监督学习的经典，是我们的主题。

他们怎么认识的呢？Jordan的导师，就是著名的链接主义核心人物Rumelhart

（参考“易图秒懂の连接主义诞生”）。在“人工智能深度学习人物关系[全]”里面我们介绍到，Hinton和Rumelhart是同事，都在Francis Crick的小组。

前言

为什么说EM算法是他们强强发力的领域呢？

这里我们讨论Hinton和统计大神Jordan的强强发力的领域。当Bayes网络发展到高级阶段， 概率图模型使得计算成为问题，由此开启了Variational Bayes领域。在“变の贝叶斯”里面， 我们解释了研究Variational Bayes，有3拨人。 第一拨人， 把物理的能量搬到了机器学习（参考 “给能力以自由吧！”）。 第二拨人， 就是Hinton，他将VB和EM算法联系了起来，奠定了现在我们看到的VB的基础。 第三拨人，就是Jordan， 他重建了VB的框架ELBO的基础。所以说EM算法扩展的VBEM算法，就是Hinton和Jordan共同发力的部分。 

Hinton曾在采访中，不无感慨的说到， 他当时研究VB和EM算法的关系的时候， 主动去请教当时的EM算法的大佬们， 结果那些人说Hinton是异想天开，神经有问题。 但是最终， 他还是突破重围， 搞定了VBEM算法，打下了VB世界最闪光的那盏灯。老爷子真心不容易！ 如果想切实深入到VB的世界， 我推荐Daphne Koller的神书“Probabilistic Graphical Models: Principles and Techniques”， 尤其其中的第8章：The Exponential Family 和第19章 Partially Observed Data。 这两章几乎是Hinton对VBEM算法研究的高度浓缩。 国内机器学习牛人王飞跃老师， 率领各路弟子花了5年时间翻译了这本神书！所以有中文版， 买了，反复阅读8、19章，要的！

为什么无监督深度学习突出成果都是Hinton和Jordan家的？

无监督深度学习，除了强化学习，主要包括BM、自动编码器AE和GAN领域。 1）这些领域中的DBN和DBM是Hinton搞的。2）AE中的经典，VAE是DP Kingma和M Welling搞得。 DP Kingma硕士导师是LeCun，LeCun的博士后导师是Hinton，并且Welling的博士后导师是Hinton。 3）而GAN是Ian Goodfellow和Yoshua Bengio的杰作， Goodfellow是Bengio的学生， 而Bengio的博士后导师是Jordan。 一句话， 无监督深度学习的经典模型几乎全是Hinton和Jordan家的。 为什么？ 因为能彻底理解EM算法到深不见底的人非Hinton和Jordan莫属。 

你现在明白彻底理解EM算法的重要性了吧？ 下面我浅薄的纵向理解（忽略EM的各种变种的横向）EM算法的9层境界，再回头反思一下Hinton和Jordan等会对EM算法的理解到何种程度， 简直叹而观止！

EM算法理解的九层境界

1. EM 就是 E + M

2. EM 是一种局部下限构造

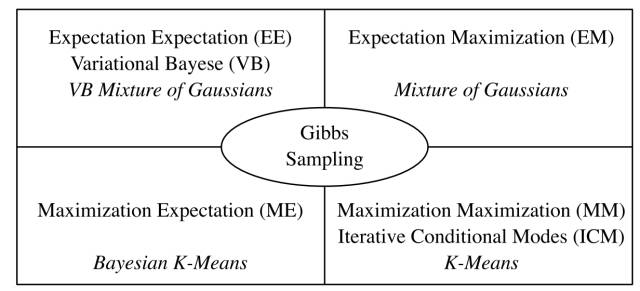
3. K-Means是一种Hard EM算法

4. 从EM 到 广义EM

5. 广义EM的一个特例是VBEM

6. 广义EM的另一个特例是WS算法

7. 广义EM的再一个特例是Gibbs抽样算法
   

8. WS算法是VAE和GAN组合的简化版

9. KL距离的统一
   

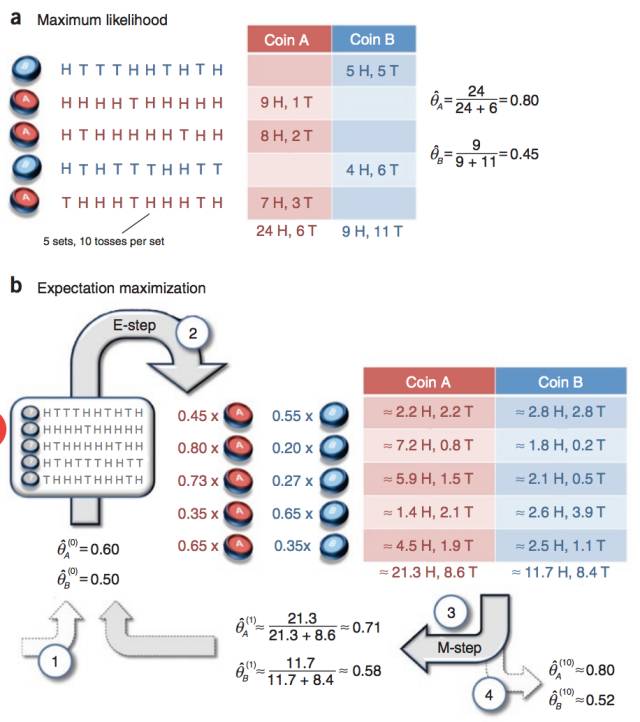
第一层境界， EM算法就是E 期望 + M 最大化

最经典的例子就是抛3个硬币，跑I硬币决定C1和C2，然后抛C1或者C2决定正反面，  然后估算3个硬币的正反面概率值。 

这个例子为什么经典， 因为它告诉我们，当存在隐变量I的时候， 直接的最大似然估计无法直接搞定。 什么是隐变量？为什么要引入隐变量？ 对隐变量的理解是理解EM算法的第一要义！Chuong B Do & Serafim Batzoglou的Tutorial论文“What is the expectation maximization algorithm?”对此有详细的例子进行分析。 

通过隐变量，我们第一次解读了EM算法的伟大！突破了直接MLE的限制（不详细解释了）。

至此， 你理解了EM算法的第一层境界，看山是山。 

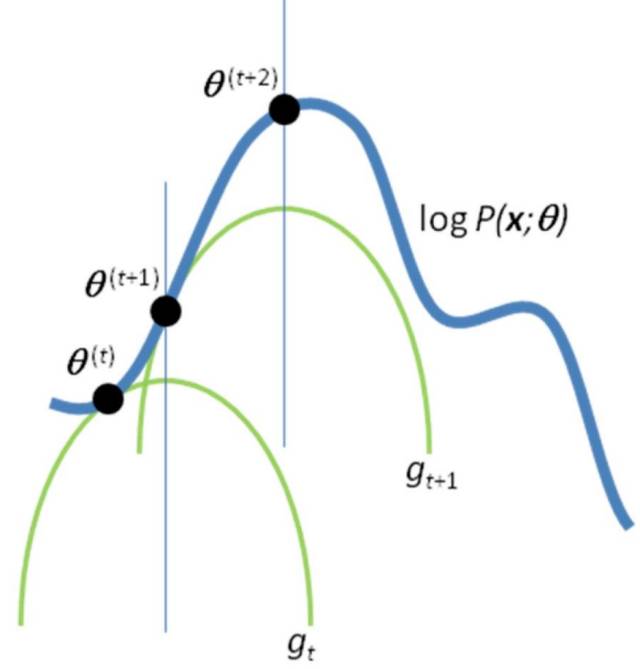
第二层境界， EM算法就一种局部下限构造

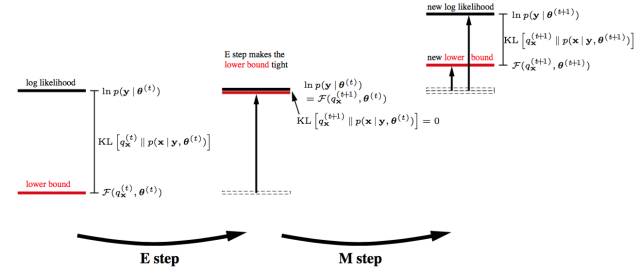
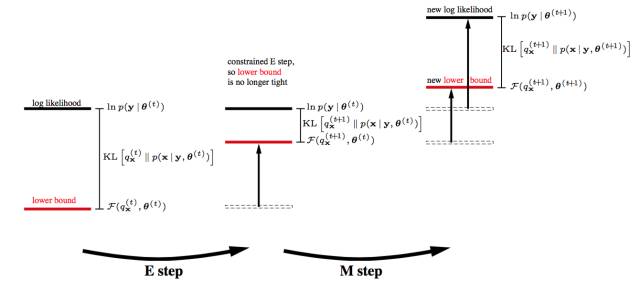
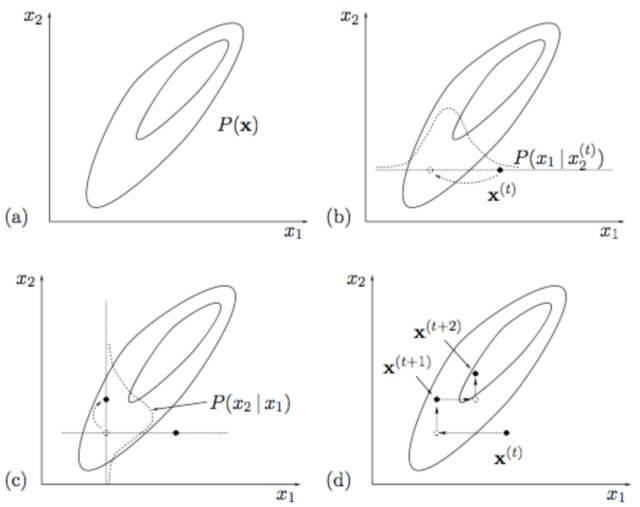
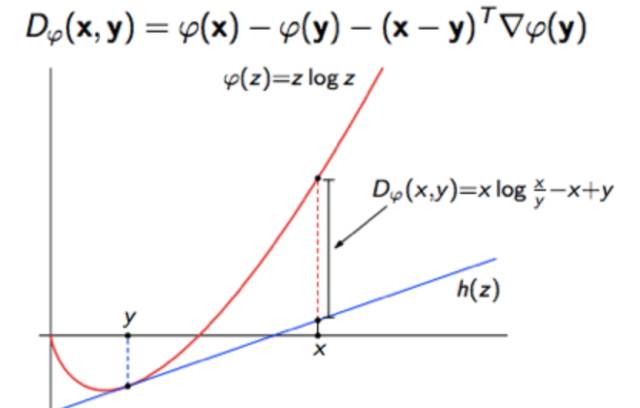
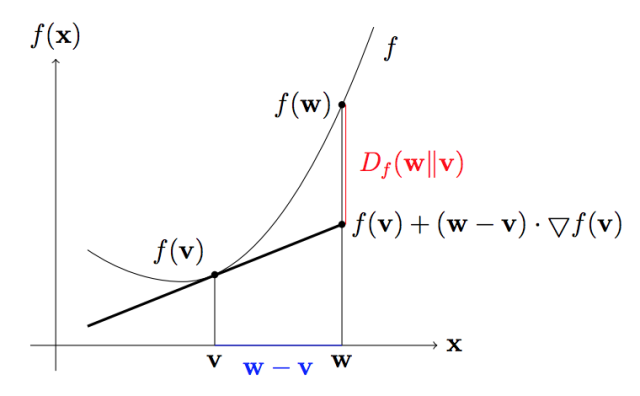
如果你再深入到基于隐变量的EM算法的收敛性证明， 基于log(x)函数的Jensen不等式构造， 我们很容易证明，EM算法是在反复的构造新的下限，然后进一步求解。 

所以，先固定当前参数， 计算得到当前隐变量分布的一个下届函数， 然后优化这个函数， 得到新的参数， 然后循环继续。 

也正是这个不停的构造下限的思想未来和VB方法联系起来了。 如果你理解了这个， 恭喜你， 进入理解EM算法的第二层境界， 看山看石。 

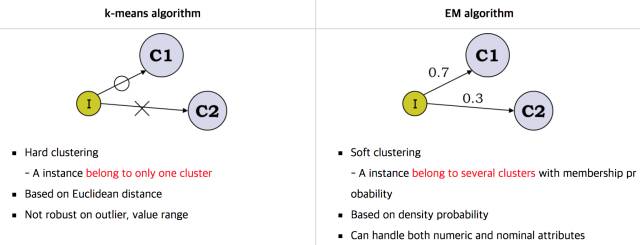
第三层境界， K-均值方法是一种Hard EM算法

在第二层境界的基础上， 你就能随意傲游EM算法用到GMM和HMM模型中去了。 尤其是对GMM的深入理解之后， 对于有隐变量的联合概率，如果利用高斯分布代入之后： 

很容易就和均方距离建立联系：

但是，能不能说K-均值就是高斯分布的EM算法呢？不是， 这里虽然拓展到了相同的距离公式， 但是背后逻辑还是不一样， 不一样在哪里呢？K-均值在讨论隐变量的决定时候，用的是dirac delta 分布， 这个分布是高斯分布的一种极限。 

如果你觉得这个扩展不太好理解， 那么更为简单直观的就是， k-均值用的hard EM算法， 而我们说的EM算法是soft EM算法。 所谓hard 就是要么是，要么不是0-1抉择。 而Soft是0.7比例是c1，0.3比例是c2的情况。 

那么充分理解了k-均值和EM算法本身的演化和差异有什么帮助呢？让你进一步理解到隐变量是存在一种分布的。 

如果你理解了这个， 恭喜你， 进入理解EM算法的第三层境界， 看山看峰。 

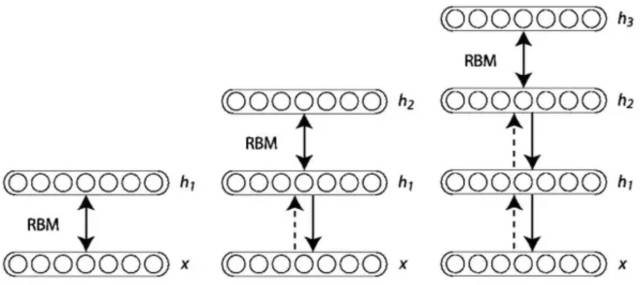
第四层境界，EM 是 广义EM的特例

通过前3层境界， 你对EM算法的理解要跨过隐变量， 进入隐分布的境界。 如果我们把前面的EM收敛证明稍微重复一下，但是引入隐分布。 

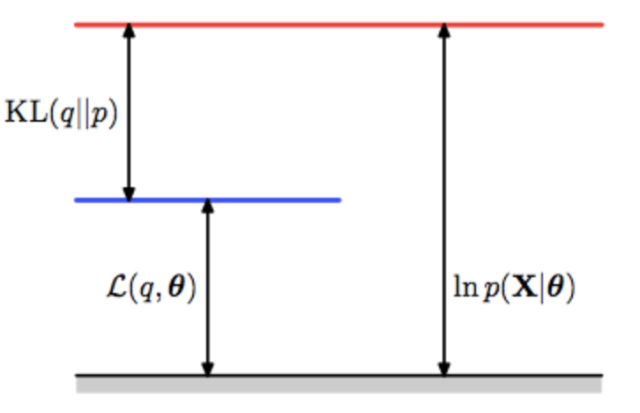
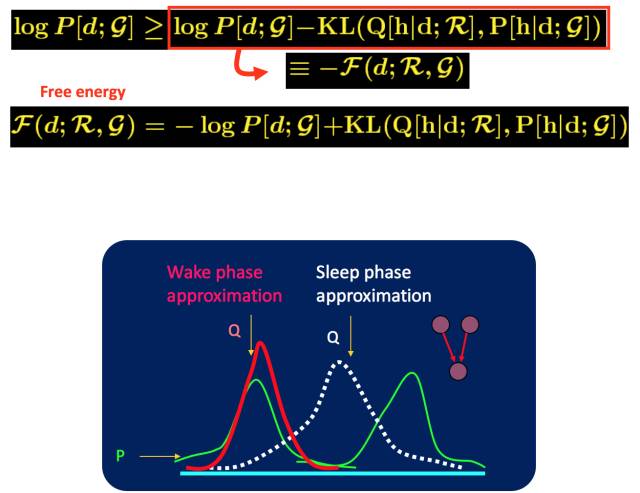
这样我们把Jensen不等收右边的部分定义为自由能（如果你对自由能有兴趣，请参考“给能量以自由吧！”，如果没有兴趣， 你就视为一种命名）。 那么E步骤是固定参数优化隐分布， M步骤是固定隐分布优化参数，这就是广义EM算法了。  

有了广义EM算法之后， 我们对自由能深入挖掘， 发现自由能和似然度和KL距离之间的关系：

所以固定参数的情况下， 那么只能最优化KL距离了， 那么隐分布只能取如下分布：

而这个在EM算法里面是直接给出的。 所以EM算法是广义EM算法的天然最优的隐分布情况。 但是很多时候隐分布不是那么容易计算的！

前面的推理虽然很简单， 但是要理解到位真心不容易， 首先要深入理解KL距离是如何被引入的？

其次要理解， 为什么传统的EM算法， 不存在第一个最优化？因为在没有限制的隐分布（天然情况下）情况下， 第一个最优就是要求：

而这个隐分布， EM算法里面是直接给出的，而不是让你证明得到的。

 

这样， 在广义EM算法中，你看到两个优化步骤，我们进入了两个优化步骤理解EM算法的境界了。 

如果你理解了这个， 恭喜你， 进入理解EM算法的第四层境界， 有水有山。 

第五层境界，广义EM的一个特例是VBEM

在隐分布没有限制的时候， 广义EM算法就是EM算法， 但是如果隐分布本身是有限制的呢？譬如有个先验分布的限制， 譬如有计算的限制呢？

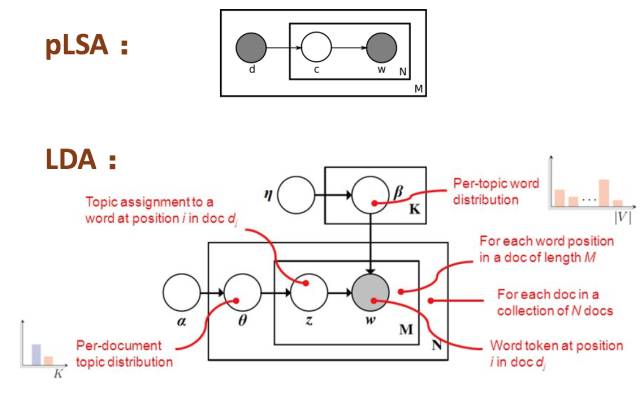
例如先验分布的限制：从pLSA到LDA就是增加了参数的先验分布！

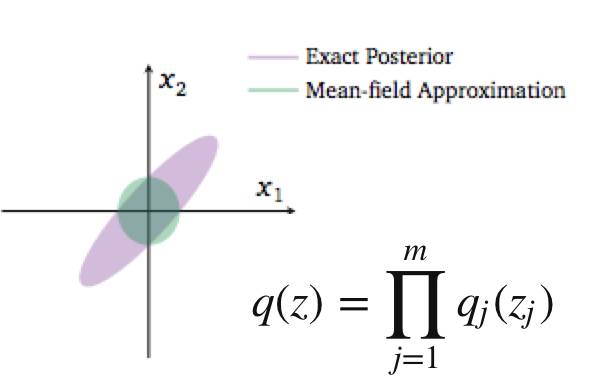
例如计算上的限制：mean-field计算简化的要求，分量独立。

诸如此类限制， 都使得广义EM里面的第一步E优化不可能达到无限制最优， 所以KL距离无法为0。 

基于有限制的理解， 再引入模型变分的思想， 根据模型m的变化， 对应参数和隐变量都有相应的分布： 

并且满足分布独立性简化计算的假设：

在变分思想下， 自由能被改写了：

这样我们就得到了VBEM算法了：

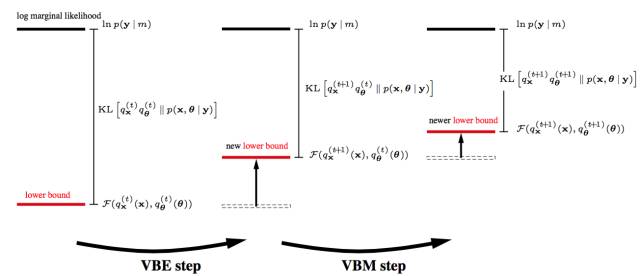
如果你理解了这个， 恭喜你， 进入理解EM算法的第五层境界， 水转山回。 

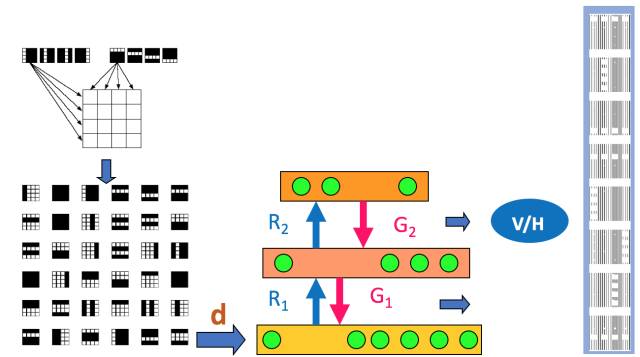
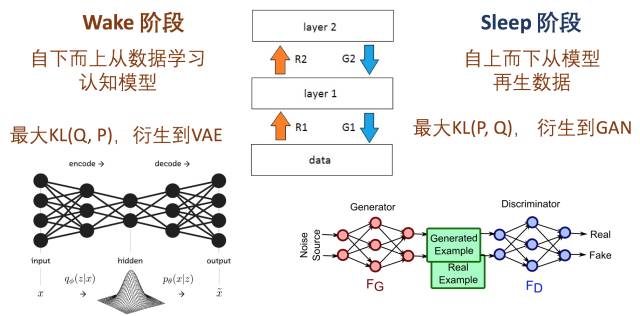
第六层境界，广义EM的另一个特例是WS算法

Hinton老爷子搞定VBEM算法后， 并没有停滞， 他在研究DBN和DBM的Fine-Tuning的时候， 提出了Wake-Sleep算法。 我们知道在有监督的Fine-Tuning可以使用BP算法， 但是无监督的Fine-Tuning，使用的是Wake-Sleep算法。 

就是这个WS算法，也是广义EM算法的一种特例。 WS算法分为认知阶段和生成阶段。 

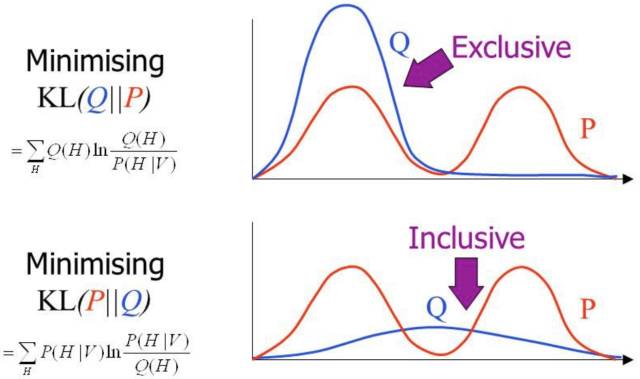
在前面自由能里面，我们将KL距离引入了， 这里刚好这两个阶段分别优化了KL距离的两种形态。 固定P优化Q，和固定Q优化P。 

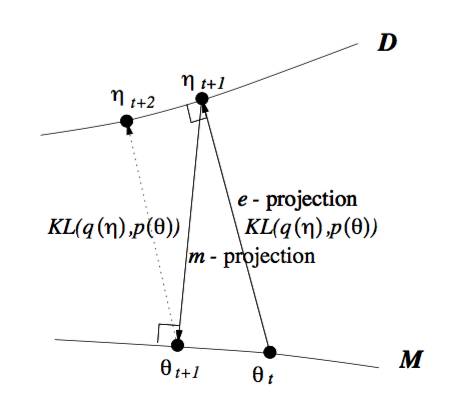
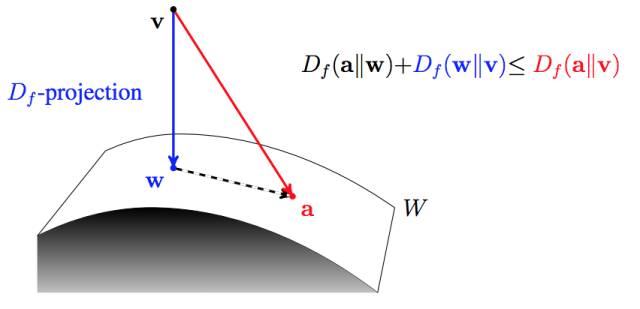
所以当我们取代自由能理解， 全部切换到KL距离的理解， 广义EM算法的E步骤和M步骤就分别是E投影和M投影。 因为要求KL距离最优， 可以等价于垂直。 而这个投影， 可以衍生到数据D的流形空间， 和模型M的流形空间。 

所以你认同WS算法是一种广义EM算法（GEM）之后， 基于KL距离再认识GEM算法。 引入了数据流形和模型流形。 引入了E投影和M投影。  

不过要注意的wake识别阶段对应的是M步骤， 而sleep生成阶段对应的E步骤。 所以WS算法对应的是广义ME算法。 

如果你理解了这个， 恭喜你， 进入理解EM算法的第六层境界， 山高水深。 

第七层境界，广义EM的再一个特例是Gibbs Sampling

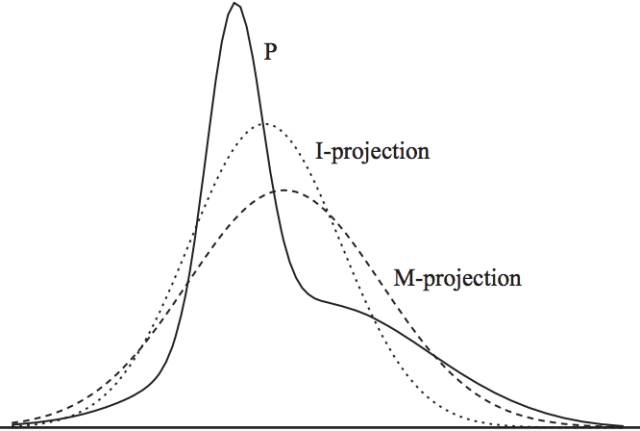
其实，前面基于KL距离的认知， 严格放到信息理论的领域， 对于前面E投影和M投影都有严格的定义。 M投影的名称是类似的，但是具体是moment projection，但是E投影应该叫I投影，具体是information projection。 

上面这种可能不太容易体会到M投影和I投影的差异， 如果再回到最小KL距离，有一个经典的比较。 可以体会M投影和I投影的差异。 上面是I投影，只覆盖一个峰。 下面是M投影， 覆盖了两个峰。 

当我们不是直接计算KL距离， 而是基于蒙特卡洛抽样方法来估算KL距离。 

有兴趣对此深入的，可以阅读论文“On Monte Carlo methods for estimating ratios of normalizing constants”

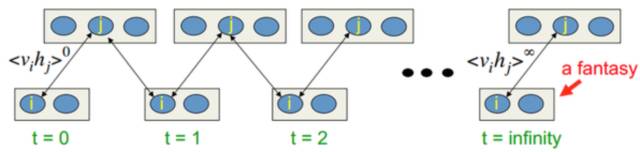
这时候， 广义EM算法，就是Gibbs Sampling了。 所以Gibbs Sampling，本质上就是采用了蒙特卡洛方法计算的广义EM算法。 

所以， 如果把M投影和I投影看成是一个变量上的最小距离点，那么Gibbs Sampling和广义EM算法的收敛过程是一致的。 

VAE的发明者，Hinton的博士后， Max Welling在论文“Bayesian K-Means as a “Maximization-Expectation” Algorithm”中， 对这种关系有如下很好的总结！

另外， Zoubin Ghahramani， Jordan的博士， 在“Factorial Learning and the EM Algorithm”等相关论文也反复提到他们之间的关系。 

这样， 通过广义EM算法把Gibbs Sampling和EM， VB， K-Means和WS算法全部联系起来了。 有了Gibbs Sampling的背书， 你是不是能更好的理解， 为什么WS算法可以是ME步骤，而不是EM的步骤呢？另外，我们知道坐标下降Coordinate Descent也可以看成一种Gibbs Sampling过程， 如果有人把Coordinate Descent和EM算法联系起来， 你还会觉得奇怪么？

现在我们发现VB和Gibbs Sampling都可以放到广义EM的大框架下， 只是求解过程一个采用近似逼近， 一个采用蒙特卡洛采样。 有了EM算法和Gibbs Sampling的关系， 现在你理解， 为什么Hinton能够发明CD算法了么？ 细节就不展开了。 

如果你理解了这个， 恭喜你， 进入理解EM算法的第七层境界， 山水轮回。 

第八层境界，WS算法是VAE和GAN组合的简化版

Jordan的弟子邢波老师，他的学生胡志挺，发表了一篇文章， On Unifying Deep Generative Models，试图通过WS算法，统一对VAE和GAN的理解。 

对VAE的理解， 变了加了正则化的KL距离， 而对于GAN的理解变成了加Jensen–Shannon 散度。  所以， 当我们把广义EM算法的自由能， 在WS算法中看成KL散度， 现在看成扩展的KL散度。  对于正则化扩展， 有很多类似论文， “Mode Regularized Generative Adversarial Networks”， “Stabilizing Training of Generative Adversarial Networks through Regularization” 有兴趣可以读读。 

所以对于VAE，类比WS算法的Wake认知阶段， 不同的是在ELBO这个VBEM目标的基础上加了KL散度作为正则化限制。 再应用再参数化技巧实现了VAE。 

而对应到GAN，类比Sleep阶段，正则化限制换了JSD距离， 然后目标KL距离也随着不同GAN的变体也可以变化。 

所以， VAE和GAN都可以理解为有特殊正则化限制的Wake-Sleep步骤， 那么组合起来也并不奇怪。 

这就是为什么那么多论文研究如何组合VAE/GAN到同一个框架下面去。目前对这方面的理解还在广泛探讨中。 

如果你理解了这个， 恭喜你， 进入理解EM算法的第八层境界， 水中有水、山外有山。  

第九层境界，KL距离的统一

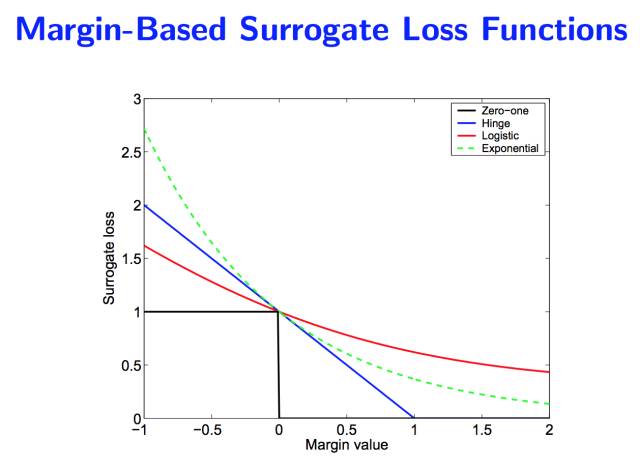
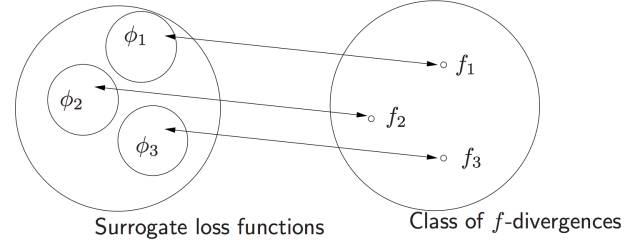
Jordan 大佬的一片论文， 开启了KL距离的统一， “On surrogate loss functions and f-divergences”。 里面对于所谓的正反KL距离全部统一到 f 散度的框架下面。 Jordan 首先论述了对于损失函数统一的Margin理论的意义。 

然后把这些损失函数也映射到  f 散度：

然后微软的 Sebastian Nowozin， 把 f-散度扩展到GAN “f-GAN: Training Generative Neural Samplers using Variational Divergence Minimization”。 

然后对正反KL散度也做了一次统一。 

对于 f-散度的理解离不开对Fenchel对偶的理解（参考“走近中神通Fenchel”）。 

除了f-散度， 还有人基于bregman散度去统一正反KL散度的认知。 KL散度就是香农熵的bregman散度。 

而Bregman散度本身是基于一阶泰勒展开的一种偏离度的度量。 

然后再基于Bregman距离去研究最小KL投影， 函数空间采用香农熵（参考“信息熵的由来”）。 

无论f-散度还是bregman散度对正反KL距离的统一， 之后的广义EM算法， 都会变得空间的最优投影的交替出现。 或许广义EM算法也成了不同流形空间上的坐标梯度下降算法而已coodinate descent。 

如果你理解了这个， 恭喜你， 进入理解EM算法的第九层境界，山水合一。  

小结

这里浅薄的介绍了理解EM算法的9层境界，托名Hinton和Jordan，着实是因为佩服他们俩和各自的弟子们对EM算法，甚至到无监督深度学习的理解和巨大贡献。想来Hinton和Jordan对此必定会有更为深刻的理解， 很好奇会到何种程度 。。。 最后依然好奇， 为啥只有他们两家的子弟能够不停的突破无监督深度学习？Hinton 老仙说， 机器学习的未来在于无监督学习！

本文经授权转载自AI2ML人工智能to机器学习，点击阅读原文查看原文。

∑编辑 | Gemini

算法数学之美微信公众号欢迎赐稿

稿件涉及数学、物理、算法、计算机、编程等相关领域，经采用我们将奉上稿酬。

投稿邮箱：math_alg@163.com