奇异值分解：协同过滤的前奏，你是SVD（下）

一：内容预告

上一篇文章复习了奇异值分解的定义、计算公式和降维方法。

这一篇来探究奇异值分解和特征分解、主成分分析法的关系，以及奇异值分解在词向量降维上的应用。

二：奇异值分解和主成分分析法

01

由特征分解到奇异值分解

（1）什么是特征分解

一个n×n的方阵A的特征分解（Eigen Decomposition )定义为：

其中V是n×n的方阵，其中每一列都是A的特征向量，∧是对角阵，其中每一个元素是A的特征值。

如果A是对称矩阵，那么A的特征分解就变成了：

其中V是正交矩阵，即V^-1=V^T。

注意是方阵才可以进行特征分解哦。

（2）推导奇异值分解

如果有一个n×m的矩阵X，我们是没法对X进行特征分解的，那么怎么由特征分解推导出奇异值分解呢？

我们注意到X^TX是m×m实对称矩阵，于是先对X^TX进行特征分解：

V的列向量是单位特征向量，对角阵∧中的对角元素是特征值，且我们对特征值进行降序排列。

假设X的秩为r，那么非零的特征值有r个。

V中的列向量（v₁, v₂, ...v_r,.. v_m）可以看成是m维空间中的m个标准正交基。X^TX特征分解就相当于一个线性变换，用标准正交基构成的矩阵V对对角矩阵进行线性变换，得到X^TX。

那么n×m的矩阵X应该也可以由一个n维空间中的n个标准正交基和一个m维空间中的m个标准正交基，对某个矩阵进行线性变换得到。

我们想办法来找到这些标准正交基。

我们就把X^TX的单位特征向量V=（v₁, v₂, ...v_r,.. v_m）作为m个标准正交基，再找另外n个标准正交基。

瞎折腾了一阵后，突然发现Xv_i与Xv_j是正交的！

太好了！这意味着我们只要把（Xv₁,Xv₂,..., Xv_m）中的非零列向量进行标准化，就可以得到另一组标准正交基了！

如果X的秩为r，那么非零列向量是（Xv₁,Xv₂,..., Xv_r）（我不知道这怎么来的，装逼失败），且满足：

于是我们对Xv_i进行标准化：

得到了r个标准正交基(u₁, u₂, ... u_r)，可是我们需要n个，还少了n-r个。

没关系，我们直接找任意n-r个列向量，填补上去，使得U=(u₁, u₂, ... u_r, ..., u_n)是一组标准正交基。

σ_i是奇异值，我们用σ_i作为对角元素来构造一个n×m维的矩阵Σ，那么X就可以用U和V这两个标准正交基组对Σ进行线性变换得到，也就是奇异值分解：X=UΣV^T。

02

奇异值分解和主成分分析法

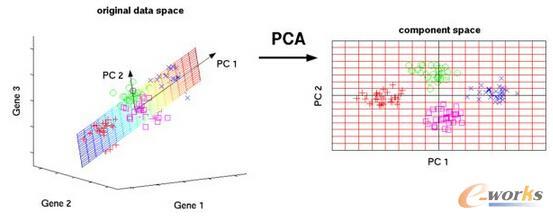
奇异值分解是主成分分析法的一种常用的解决方案。

如果数据集X是一个n×m的矩阵，n是变量的个数，m是样本的数量，那么进行主成分分析，也就是用奇异值分解的左奇异矩阵或者右奇异矩阵的装置作为主成分分析法中的转换矩阵，去乘以数据集X，从而得到主成分矩阵Y。

（1）为什么用奇异值分解

可是在《主成分分析法：NLPer的断舍离（上篇）》中，我们明白了，可以求出X的协方差矩阵的单位特征向量矩阵E，用E的转置E^T作为转换矩阵P，然后由PX=Y得到主成分矩阵，再挑出前k主成分就可以做到降维。

那我们直接去求E不就好了吗？干嘛还要把奇异值分解拉扯进来？

这是因为求解n维矩阵XX^T的特征值和特征向量的算法复杂度为O(n³)，因此如果X是高维的数据，也就是n非常大时，进行主成分分析就要计算超大矩阵的特征值。

这就出现了算法复杂度过高，计算效率太低的问题。

可是奇异值分解也要对矩阵X^TX进行特征分解来求右奇异矩阵V啊，算法复杂度不也是O(n³)？

是这样的，不过对高维矩阵进行奇异值分解时，有一些更高效的算法，不用采取暴力特征分解的方式。

（2）奇异值分解与主成分分析法等价

我们先按照主成分分析法的步骤，对XX^T进行特征分解，得到：

然后对X进行奇异值分解，沿用前面的符号体系，得到X=UΣV^T，把X的奇异值分解代入到上面的特征分解式中：

由于在主成分分析法中我们用E^T作为转换矩阵P，那么从上面的推导可知，可以用X的左奇异矩阵U的转置U^T作为转换矩阵P，来求出主成分矩阵Y，U^TX=Y。

（3）用奇异值分解做主成分降维

X的奇异值分解还可以简化地写成X=U₁SV₁^T，同样代入XX^T的特征分解中，得到：XX^T=U₁SS^TU₁^T。

U₁=(u₁, u₂, ...u_r)是n×r的矩阵，那么U₁^T是一个r×n的矩阵，U₁^TX就把X的特征从n维降至了r维。

进一步，我们在前面用分块矩阵的思想，把U₁分块为U₁=[U₁₁, U₁₂]，U₁₁^T是一个d×n维的矩阵，那么用U₁₁^T作为转换矩阵，就可以把X的特征进一步压缩至d维。

 （4）其他补充

如果你看了其他博主写的博客，会发现有些是用右奇异矩阵V的转置V^T来作为特征压缩的转换矩阵，和本文不一样。

这是因为那些博客把有m个样本，n维特征的数据集写成了m×n的矩阵X，而本文把数据集写成n×m的矩阵，所以那些博客是用右奇异矩阵V，而本文是用左奇异矩阵U。

三：奇异值分解和词向量降维

我们来看怎么把奇异值分解用在词向量降维上。

如果我们手头有一份文本数据集，里头有m篇文档，总共有n个不重复的词，那么我们可以通过统计文档中所有词出现的次数，整理成一个矩阵X，来构造词向量。

一般有两种方法来构造词向量矩阵：

一是TF-IDF，词向量矩阵是n×m维的，行向量是每个词的词向量；

二是基于窗口的共现矩阵，如果窗口是1，那么词向量矩阵是n×n维的，行向量是每个词的词向量。

这两种词向量的表示方法存在很大的问题：数据稀疏和词表维度过高。

想象一下，如果文档有100万篇，词有5万个，那会是多么恐怖的一个场景。

因此我们非常有必要运用奇异值分解，对词向量矩阵进行降维。

01

对TF-IDF词向量矩阵降维

TF-IDF不用多解释了，由每个词的词频和逆文档频率计算得到每个词的TF-IDF，然后所有词的TF-IDF构成词向量矩阵X^n×m。

这个矩阵太大了，我们对这个矩阵X进行奇异值分解得到U₁SV₁^T，U₁是n×r的矩阵，我们用U₁的行向量作为n个词的词向量，就实现了对文档数量维度的压缩。

如果还嫌词表维度太高，那么我们可以继续降维，从U₁中拿出前d个列向量，组成新的n×d维的词向量矩阵U₁₁，行向量作为降到d维后每个词的词向量。

d取多少合适呢？

我们可以用奇异值的平方和计算降到d维后的剩余的信息量。如果我们希望保留85%的信息，那么就取以下公式大于或等于85%时的d值，作为降维后的维度。

02

对词共现矩阵降维

这种方法是用一个相关性矩阵来构造词向量矩阵，叫做共现矩阵。

假设有3个句子（看成三篇文档也没毛病），一共8个不重复的词（把标点也算上），窗口设定为1，也就是把句子拆成一个个的词。

• I enjoy flying.

• I like NLP.

• I like deep learning

 那么共现矩阵就是一个8维的方阵X：

同样用奇异值分解，把X分解为X=U₁SV₁^T，然后用U₁的行向量作为每次词的词向量，就把词向量的维度从n维降到了r维。

如果觉得还太高了，那么可以按照TF-IDF中的做法，继续进行降维。

  

参考资料：

1、《A Tutorial on Principal Component Analysis. Derivation, Discussion and Singular Value Decomposition》

2、《A Singularly Valuable Decomposition: The SVD of a Matrix 》

END

推荐阅读

AINLP年度阅读收藏清单

百度PaddleHub NLP模型全面升级，推理性能提升50%以上

斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用

数学之美中盛赞的 Michael Collins 教授，他的NLP课程要不要收藏？

自动作诗机&藏头诗生成器：五言、七言、绝句、律诗全了

From Word Embeddings To Document Distances 阅读笔记

模型压缩实践系列之——bert-of-theseus，一个非常亲民的bert压缩方法

这门斯坦福大学自然语言处理经典入门课，我放到B站了

可解释性论文阅读笔记1-Tree Regularization

征稿启示 | 稿费+GPU算力+星球嘉宾一个都不少

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLPer(id：ainlper)，备注工作/研究方向+加群目的。