强化学习中无处不在的贝尔曼最优性方程,背后的数学原理为何?
作者 | Vaibhav Kumar
编译 | 亚希伯恩•菲
编辑 | 丛末
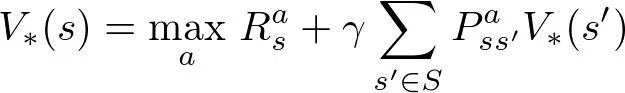
一、本文将涉及到的数学符号
S 表示状态空间
V 表示值函数
V* 表示最优值函数
V(s) 表示值函数在状态为 s时的取值
π 表示策略
π* 表示最优策略
-
π(s) 返回在状态为 s 时策略π所采取的行动 -
P 表示转移概率矩阵 -
A 表示所有可能行动的集合
二、预备知识
马尔可夫决策过程(MDP)
贝尔曼方程式以及如何使用迭代法求解此方程
RL基础,诸如价值函数,奖励,策略,折现因子等概念
线性代数
向量求导
三、理解贝尔曼方程的几大要点
对于任何有限的MDP,都存在一个最佳策略π*,满足其他所有可能的策略π都不会比这个策略更好。
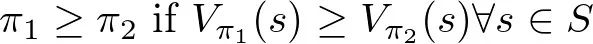
1. 不动点问题
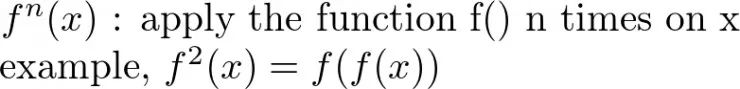
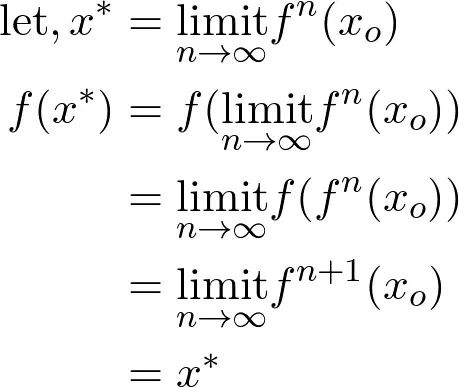
https://gist.github.com/TimeTraveller-San/8e37399d4740928a258f395413bde2e7/raw/c48fecd50fa29634eea144917f92787c3ccd7bf3/Fixed%20point%20problem.ipynb
2. 度量空间
单位性:d(x,x) = 0
非负性:d(x, y) >0
对称性:d(x,y) = d(y,x)
三角不等式:d(x,z) ≤ d(x,y)+d(y,x)
3. 柯西序列
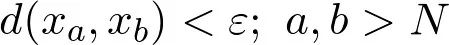
4. 完备度量空间
5. 压缩映像
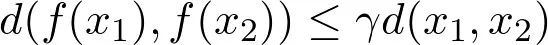
6. 巴拿赫不动点定理
压缩映射将集合中元素聚集到一起。
不停地运用这个压缩映射,我们会得到一个柯西序列。
完备度量空间中的柯西序列始终会收敛到自身中的一个值。
令(X, d)是一个完备的度量空间,函数f: X->X是一个压缩映射,则f具有唯一一个不动点 x*∈ X (即,f(x *)=x *) ,使得序列 f(f(f(…f(x))))收敛至x *。
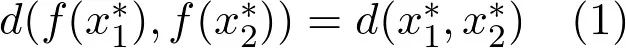
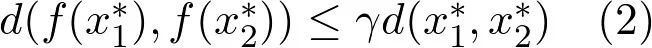
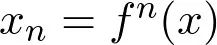
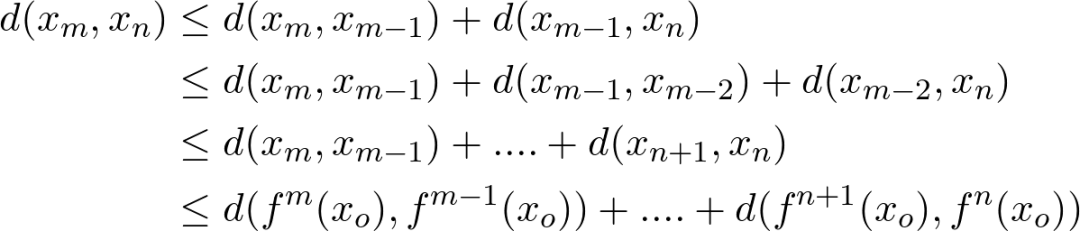
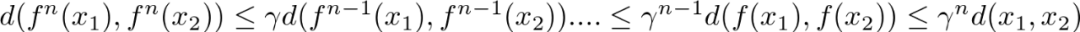
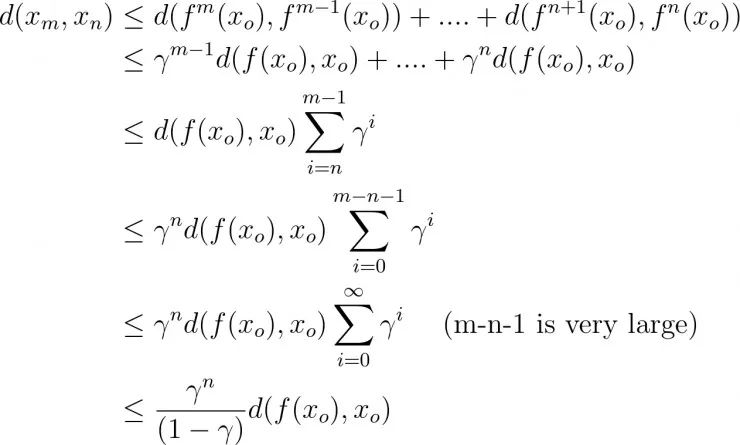
四、回到贝尔曼最优性方程
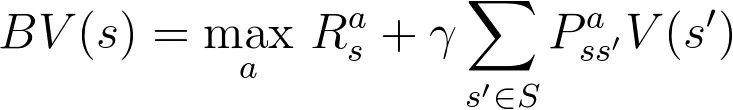
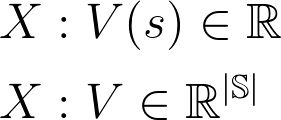
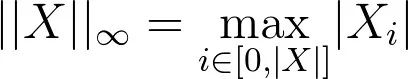
定理:贝尔曼算子B是有限空间(X, L-infinity)上的压缩映射
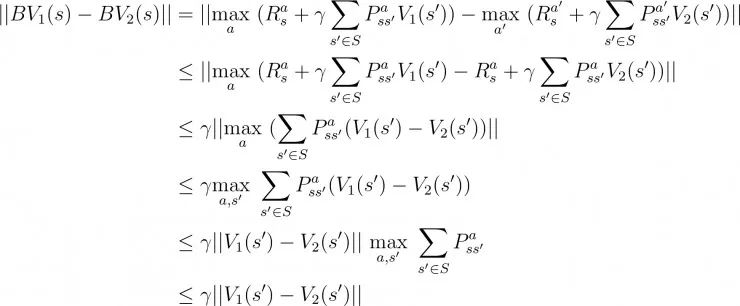
在上面的第二步中,我们通过用a代替第二个值函数中的a'来引入不等式。这是因为通过将最优动作a替换为其他动作 a',我们降低了其总价值,从而引入了不等式。
在上面的第四步中,我们通过在状态空间 s'上取最大值来移除L-无穷范数(回想一下在前面我们关于值函数的L-无穷范数的定义)
在最后一步中,因为概率和始终为1,我们消去了求和号。
1、(X, L-infinity) 是一个完备的度量空间
2、贝尔曼算子B是压缩映射
作者的博客:https://towardsdatascience.com/reinforcement-learning-temporal-difference-sarsa-q-learning-expected-sarsa-on-python-9fecfda7467e
Github 地址:https://github.com/TimeTraveller-San/RL_from_scratch
五、总结
直播预告
【时间】2020年2月22日晚20:00