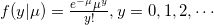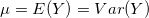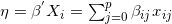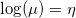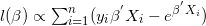数据分析师应该知道的16种回归方法：泊松回归

从这篇开始，将给大家分享三类计数回归模型：泊松回归，负二项回归，准泊松回归。先从泊松回归开始，泊松回归是最常用的计数回归模型，它是广义线性回归模型的一种，其因变量服从泊松分布。泊松回归常用来对非负整数随机变量建模。

泊松分布

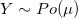
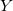
设随机变量,则的概率密度函数为：

泊松分布一个重要的特征是：唯一的参数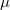，即是均值又是方差，即

泊松回归

在泊松回归中，解释变量对响应变量的平均值进行建模。因为响应变量的均值必须是正的但解释变量的线性组合

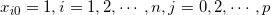
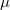
其中，可取任何值，因此我们需要寻找参数的联结函数保证回归等式成立。标准的联结函数是自然对数，即

将上述关系带入泊松分布的概率密度函数中，其对数似然函数为：

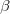
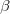
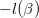
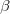
虽然对求导后不能获得关于的解析表达式，但为凸函数，因此我们可以采用梯度下降的方法获得的最优值。

案例

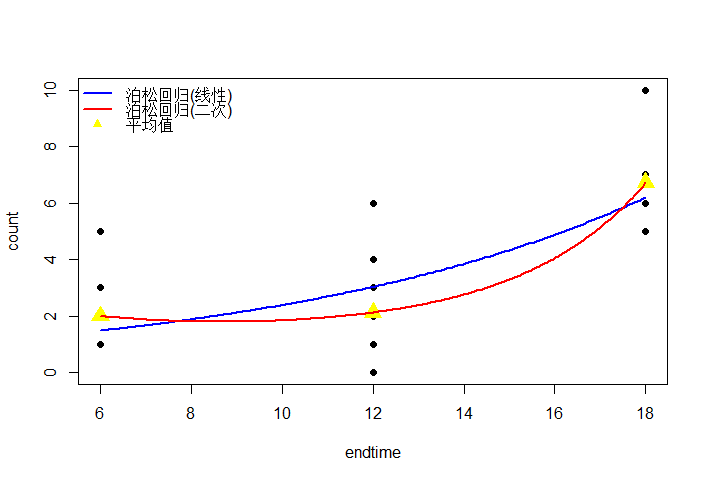
ACF是一种异常管状结构，它们是肿瘤的前兆。在一项实验中，研究人员将22只老鼠暴露在一种致癌物质中，然后计算出老鼠结肠中ACFs的数量。小鼠被分成三组，从首次接触致癌物质开始，三组分别是6、12或18周记录ACFs的数量。数据在DAAG包的ACF1数据集中，包含count(ACFs的数量)和endtime(结束时间)两个变量。

library(DAAG)
attach(ACF1)
plot(count ~ endtime, pch = 16,cex=2,col='red')
acf1.glm = glm(count ~ endtime, family = poisson)
acf2.glm = glm(count ~ endtime + I(endtime^2), family = poisson)
plot(count ~ endtime, pch = 16)
means = sapply(split(count, endtime), mean)
unq = unique(endtime)
points(unq, means, col = "yellow", pch = 17, cex = 2)
u = seq(6, 18, length = 201)
dfu = data.frame(endtime = u)
eta1 = predict(acf1.glm, dfu)
eta2 = predict(acf2.glm, dfu)
lines(u, exp(eta1), col = "blue",lwd=2)
lines(u, exp(eta2), col = "red",lwd=2)
legend('topleft',c('泊松回归(线性)','泊松回归(二次)','平均值'),
       col=c('blue','red','yellow'),lty=c(1,1,NA),pch=c(NA,NA,17),
       bty='n',lwd=c(2,2,NA))
detach(ACF1)

从图可以发现二次泊松回归可以很好拟合每组小鼠ACFs数的平均值。

推荐阅读

数据分析师应该知道的16种回归方法：支持向量回归

数据分析师应该知道的16种回归方法：定序回归

reticulate: R interface to Python

谈谈大数据的那点事 （12）——如何理解大数据和分析大数据

从零开始深度学习第10讲：三维卷积、池化与全连接

R语言做并行爬虫（案例说明）

R语言爬虫常用方法总结（以案例说明）

使用jupyter notebook搭建数据科学最佳交互式环境

长按二维码关注“数萃大数据”