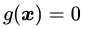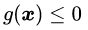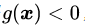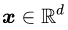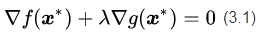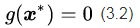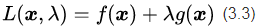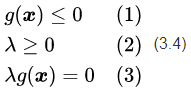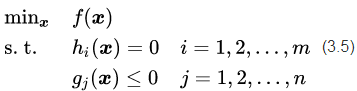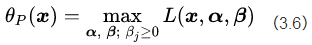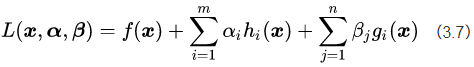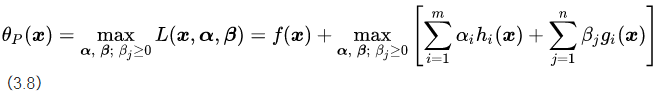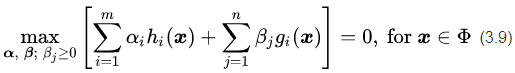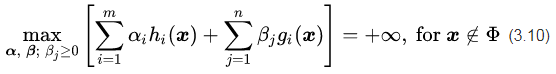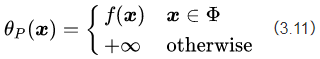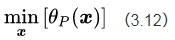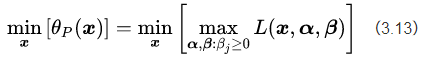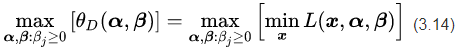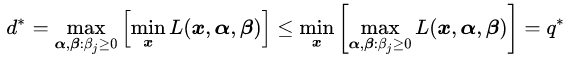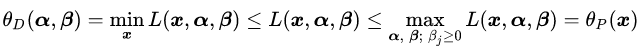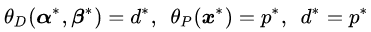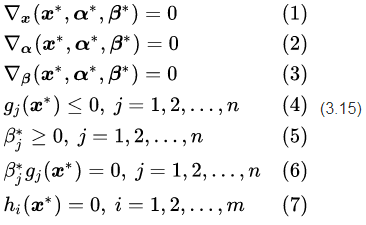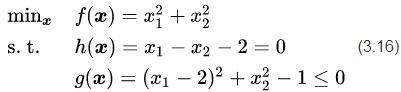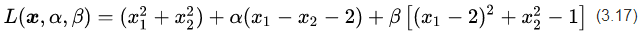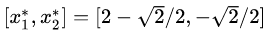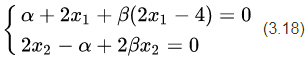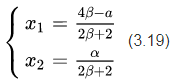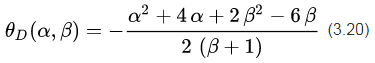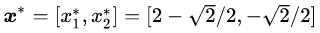零基础学SVM—Support Vector Machine系列之二
本文原作者耳东陈,本文原载于作者的知乎文章。AI 研习社已获得转载授权。
有约束最优化问题的数学模型
就像我们在第二部分结尾时提到的,SVM问题是一个不等式约束条件下的优化问题。绝大多数模式识别教材在讨论这个问题时都会在附录中加上优化算法的简介,虽然有些写得未免太简略,但看总比不看强,所以这时候如果你手头有一本模式识别教材,不妨翻到后面找找看。结合附录看我下面写的内容,也许会有帮助。
我们先解释一下我们下面讲解的思路以及重点关注哪些问题:
1)有约束优化问题的几何意象:闭上眼睛你看到什么?
2)拉格朗日乘子法:约束条件怎么跑到目标函数里面去了?
3)KKT条件:约束条件是不等式该怎么办?
4)拉格朗日对偶:最小化问题怎么变成了最大化问题?
5)实例演示:拉格朗日对偶函数到底啥样子?
6)SVM优化算法的实现:数学讲了辣么多,到底要怎么用啊?
3.1 有约束优化问题的几何意象
约束条件一般分为等式约束和不等式约束两种,前者表示为![]() (注意这里的X跟第二章里面的样本x没有任何关系,只是一种通用的表示);后者表示为
(注意这里的X跟第二章里面的样本x没有任何关系,只是一种通用的表示);后者表示为![]() (你可能会问为什么不是
(你可能会问为什么不是![]() ,别着急,到KKT那里你就明白了)。
,别着急,到KKT那里你就明白了)。
假设![]() (就是这个向量一共有d个标量组成),则
(就是这个向量一共有d个标量组成),则![]() 的几何意象就是d维空间中的d-1维曲面,如果函数
的几何意象就是d维空间中的d-1维曲面,如果函数![]() 是线性的,
是线性的,![]() 则是个d-1维的超平面。那么有约束优化问题就要求在这个d-1维的曲面或者超平面上找到能使得目标函数最小的点,这个d-1维的曲面就是“可行解区域”。
则是个d-1维的超平面。那么有约束优化问题就要求在这个d-1维的曲面或者超平面上找到能使得目标函数最小的点,这个d-1维的曲面就是“可行解区域”。
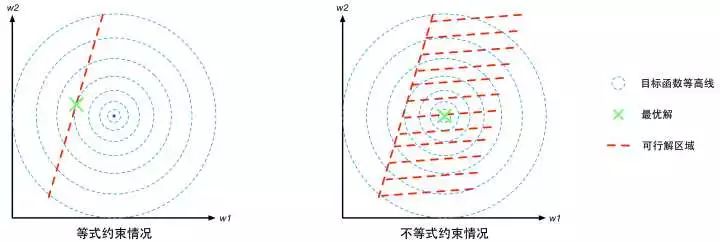
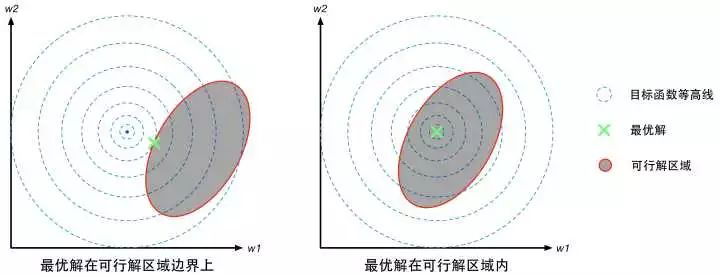
对于不等式约束条件,![]() ,则可行解区域从d-1维曲面扩展成为d维空间的一个子集。我们可以从d=2的二维空间进行对比理解。等式约束对应的可行解空间就是一条线;不等式约束对应的则是这条线以及线的某一侧对应的区域,就像下面这幅图的样子(图中的目标函数等高线其实就是等值线,在同一条等值线上的点对应的目标函数值相同)。
,则可行解区域从d-1维曲面扩展成为d维空间的一个子集。我们可以从d=2的二维空间进行对比理解。等式约束对应的可行解空间就是一条线;不等式约束对应的则是这条线以及线的某一侧对应的区域,就像下面这幅图的样子(图中的目标函数等高线其实就是等值线,在同一条等值线上的点对应的目标函数值相同)。
图3 有约束优化问题的几何意象图
3.2 拉格朗日乘子法
尽管在3.1节我们已经想象出有约束优化问题的几何意象。可是如何利用代数方法找到这个被约束了的最优解呢?这就需要用到拉格朗日乘子法。
首先定义原始目标函数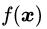
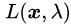
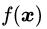
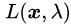
1)最优解的特点分析
这里比较有代表性的是等式约束条件(不等式约束条件的情况我们在KKT条件里再讲)。我们观察一下图3中的红色虚线(可行解空间)和蓝色虚线(目标函数的等值线),发现这个被约束的最优解恰好在二者相切的位置。这是个偶然吗?我可以负责任地说:“NO!它们温柔的相遇,是三生的宿命。”为了解释这个相遇,我们先介绍梯度的概念。梯度可以直观的认为是函数的变化量,可以描述为包含变化方向和变化幅度的一个向量。然后我们给出一个推论:
推论1:“在那个宿命的相遇点
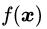
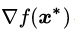
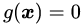
关于推论1的粗浅的论证如下:
如果梯度矢量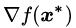
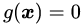

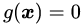

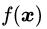
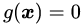
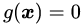

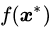

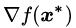
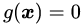
推论2:“函数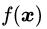
推论2的粗浅论证:与推论1 的论证基本相同,如果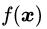
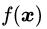
根据推论1和推论2,函数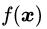

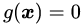
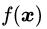
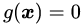

让我们再进一步,约束条件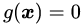
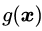
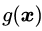

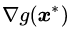
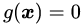
到此我们可以将目标函数和约束条件视为两个具有平等地位的函数,并得到推论3:
推论3:“函数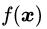
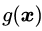


于是我们可以写出公式(3.1),用来描述最优解
这里增加了一个新变量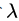


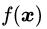

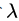
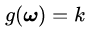
把公式(3.1)和(3.2)放在一起,我们有d+1个方程,解d+1个未知数,方程有唯一解,这样就能找到这个最优点
2)构造拉格朗日函数
虽然根据公式(3.1)和(3.2),已经可以求出等式约束条件下的最优解了,但为了在数学上更加便捷和优雅一点,我们按照本节初提到的思想,构造一个拉格朗日函数,将有约束优化问题转为无约束优化问题。拉格朗日函数具体形式如下:
新的拉格朗日目标函数有两个自变量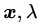
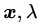
至此,我们说明白了“为什么构造拉格朗日目标函数可以实现等式约束条件下的目标优化问题的求解”。可是,我们回头看一下公式(2.14),也就是我们的SVM优化问题的数学表达。囧,约束条件是不等式啊!怎么办呢?
3.3 KKT条件
对于不等式约束条件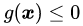

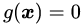
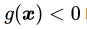
第一种情况:最优解在边界上,就相当于约束条件就是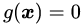
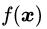
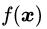

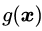

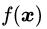
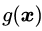
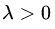
图4:不等式约束条件下最优解位置分布的两种情况
第二种情况:如果在区域内,则相当于约束条件没有起作用,因此公式(3.3)的拉格朗日函数中的参数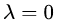
其中第一个式子是约束条件本身。第二个式子是对拉格朗日乘子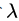
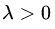
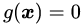
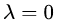
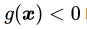
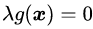
推导除了KKT条件,感觉有点奇怪。因为本来问题的约束条件就是一个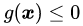
1)KKT条件是对最优解的约束,而原始问题中的约束条件是对可行解的约束。
2)KKT条件的推导对于后面马上要介绍的拉格朗日对偶问题的推导很重要。
3.4 拉格朗日对偶
接下来让我们进入重头戏——拉格朗日对偶。很多教材到这里自然而然的就开始介绍“对偶问题”的概念,这实际上是一种“先知式”的教学方式,对于学生研究问题的思路开拓有害无益。所以,在介绍这个知识点之前,我们先要从宏观的视野上了解一下拉格朗日对偶问题出现的原因和背景。
按照前面等式约束条件下的优化问题的求解思路,构造拉格朗日方程的目的是将约束条件放到目标函数中,从而将有约束优化问题转换为无约束优化问题。我们仍然秉承这一思路去解决不等式约束条件下的优化问题,那么如何针对不等式约束条件下的优化问题构建拉格朗日函数呢?
因为我们要求解的是最小化问题,所以一个直观的想法是如果我能够构造一个函数,使得该函数在可行解区域内与原目标函数完全一致,而在可行解区域外的数值非常大,甚至是无穷大,那么这个没有约束条件的新目标函数的优化问题就与原来有约束条件的原始目标函数的优化是等价的问题。
拉格朗日对偶问题其实就是沿着这一思路往下走的过程中,为了方便求解而使用的一种技巧。于是在这里出现了三个问题:1)有约束的原始目标函数优化问题;2)新构造的拉格朗日目标函数优化问题;3)拉格朗日对偶函数的优化问题。我们希望的是这三个问题具有完全相同的最优解,而在数学技巧上通常第三个问题——拉格朗日对偶优化问题——最好解决。所以拉格朗日对偶不是必须的,只是一条捷径。
1)原始目标函数(有约束条件)
为了接下来的讨论,更具有一般性,我们把等式约束条件也放进来,进而有约束的原始目标函数优化问题重新给出统一的描述:
公式(3.5)表示m个等式约束条件和n个不等式约束条件下的目标函数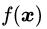
2)新构造的目标函数(没有约束条件)
接下来我们构造一个基于广义拉格朗日函数的新目标函数,记为:
其中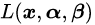
这里,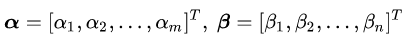
我们对比公式(3.5)中的约束条件,将论域范围分为可行解区域和可行解区域外两个部分对公式(3.8)的取值进行分析,将可行解区域记为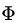
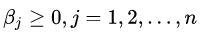
可行解区域内:由于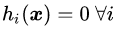
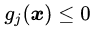
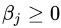
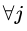
可行解区域外:代表公式(3.5)中至少有一组约束条件没有得到满足。如果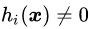
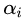
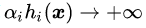
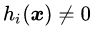
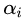
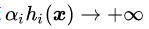
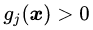
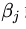
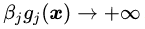
把公式(3.8),(3.9)和(3.10)结合在一起就得到我们新构造的目标函数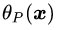
此时我们回想最初构造新目标函数的初衷,就是为了建立一个在可行解区域内与原目标函数相同,在可行解区域外函数值趋近于无穷大的新函数。看看公式(3.11),yeah,我们做到了。
现在约束条件已经没了,接下来我们就可以求解公式(3.12)的问题
这个问题的解就等价于有约束条件下的原始目标函数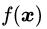
3)对偶问题
尽管公式(3.12)描述的无约束优化问题看起来很美好,但一旦你尝试着手处理这个问题,就会发现一个麻烦。什么麻烦呢?那就是我们很难建立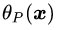
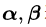
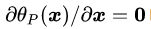

要解决这个问题,就得用一点数学技巧了,这个技巧就是对偶问题。我们先把公式(3.6)和公式(3.12)放在一起,得到关于新构造的目标函数的无约束优化的一种表达:
然后我们再构造另一个函数,叫做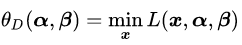
对比公式(3.13)和(3.14),发现两者之间存在一种对称的美感。所以我们就把(3.14)称作是(3.13)的对偶问题。现在我们可以解释一下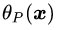
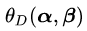

4)对偶问题同解的证明
对偶问题和原始问题到底有没有相同的最优解呢?关于这个问题的根本性证明其实没有在这里给出,而且在几乎我看到的所有有关SVM的资料里都没有给出。但我比较厚道的地方是我至少可以告诉你哪里能找到这个证明。在给出证明的链接地址之前,我们先给一个定理,帮助大家做一点准备,同时也减少一点看那些更简略的资料时的困惑。
定理一:对于任意α,β和χ有:
定理一的证明:
即
所以
即:
这里的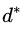
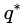
定理一既引入了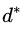
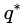

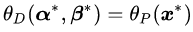
这个推论实际上已经涉及了原始问题与对偶问题的“强对偶性”。当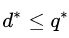
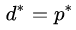
如果我们希望能够使用拉格朗日对偶问题替换原始问题进行求解,则需要“强对偶性”作为前提条件。于是我们的问题变成了什么情况下,强对偶性才能够在SVM问题中成立。关于这个问题我们给出定理二:
定理二:对于原始问题和对偶问题,假设函数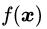

为凸函数,等式约束条件中的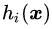
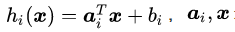
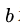
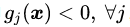


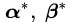
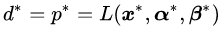
再次强调一下,公式(3.15)是使
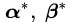
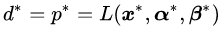

定理二的证明详见 《Convex Optimization》, by Boyd and Vandenberghe. Page-234, 5.3.2节。(http://dwz.cn/6P8gpT)
关于拉格朗日对偶的一些参考资料:
1. 简易解说拉格朗日对偶(Lagrange duality)( http://dwz.cn/6P8k8s),这一篇对对偶问题的来龙去脉说的比较清楚,但是在强对偶性证明方面只给出了定理,没有给出证明过程,同时也缺少几何解释。
2.优化问题中的对偶性理论(http://xiaoyc.com/duality-theory-for-optimization/),这一篇比较专业,关于对偶理论的概念,条件和证明都比较完整,在数学专业文献里属于容易懂的,但在我们这种科普文中属于不太好懂的,另外就是论述过程基本跟SVM没啥关系。
3.5 拉格朗日对偶函数示例
尽管上述介绍在代数层面已经比较浅显了,但是没有可视化案例仍然不容易建立起直观的印象。所以我尽可能的在这里给出一个相对简单但是有代表性的可视化案例。
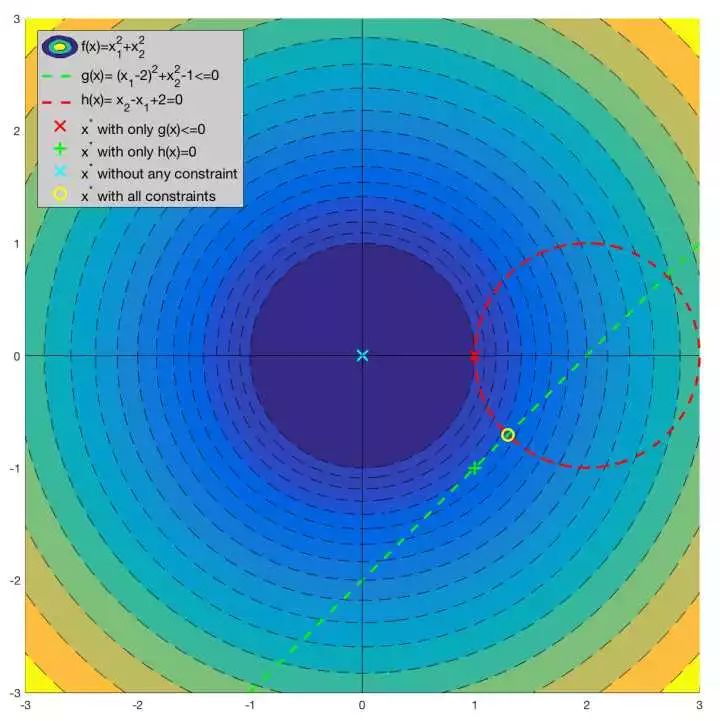
图5:有约束条件下的最优化问题可视化案例
图5中的优化问题可以写作:
之所以说这个案例比较典型是因为它与线性SVM的数学模型非常相似,且包含了等式和不等式两种不同的约束条件。更重要的是,这两个约束条件在优化问题中都起到了作用。如图5所示,如果没有任何约束条件,最优解在坐标原点(0, 0)处(青色X);如果只有不等式约束条件 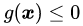
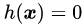
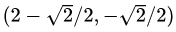
针对这一问题,我们可以设计拉格朗日函数如下:
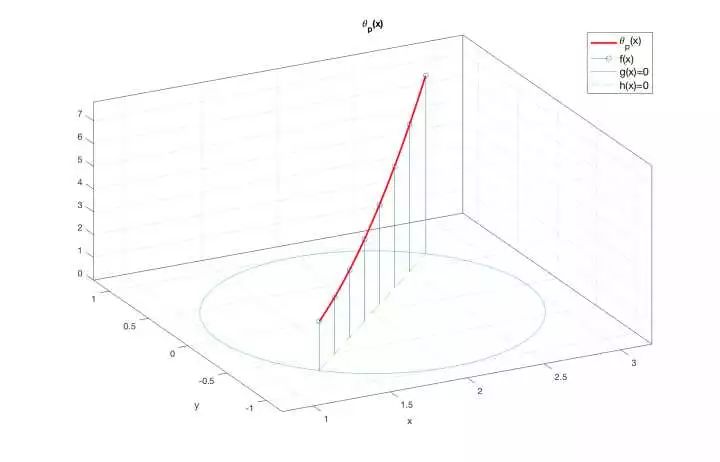
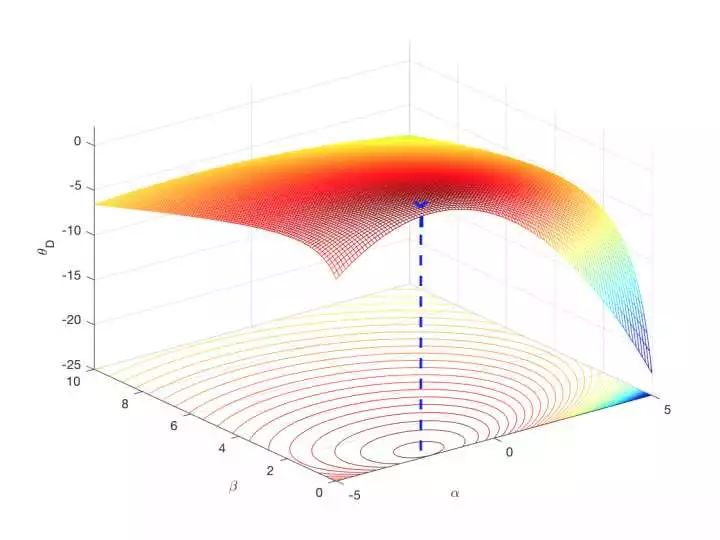
根据公式(3.11),函数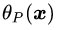
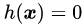
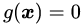
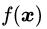
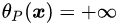
图6: 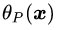
(需要注意的是,此处不能使用对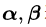
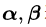
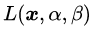
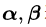
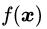
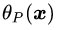

由于该最优解是在 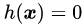
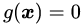
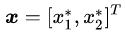
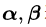
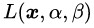
然而这个最优解是依靠几何推理的方式找到的,对于复杂的问题,这种方法似乎不具有可推广性。
那么,我们不妨尝试一下,用拉格朗日对偶的方式看看这个问题。我们将 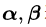
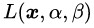
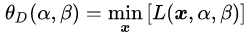
分别求偏导,令其等于0,有:
可以解得:
将(3.19)带入(3.17)可以得到:
考虑到(3.15)中的条件(5),我们将函数(3.20)在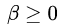
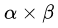
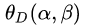
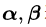
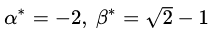
最后通过对比,我们看到拉格朗日原始问题和对偶问题得到了相同的最优解(原始问题的最优解中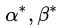
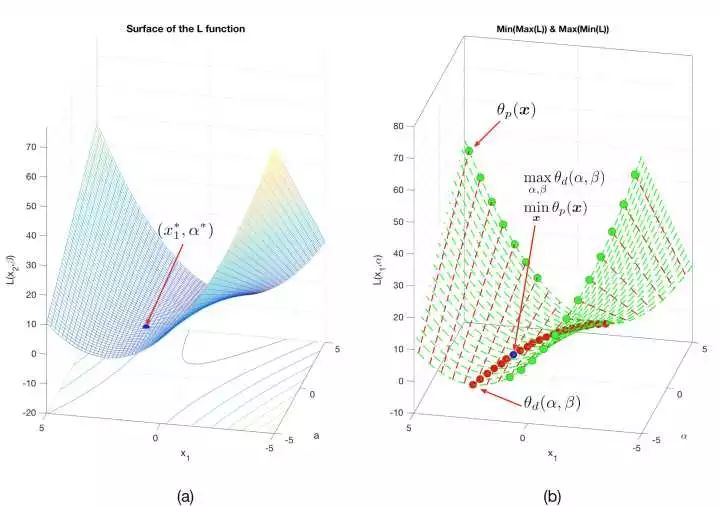
最后,我来解释一下鞍点的问题。鞍点的概念大家可以去网上找,形态上顾名思义,就是马鞍的中心点,在一个方向上局部极大值,在另一个方向上局部极小值。这件事跟我们的拉格朗日函数有什么关系呢?由于这个例子中的拉格朗日函数包含 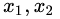
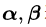
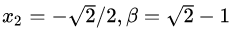
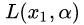
图8: 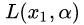
图8(a)中的最优点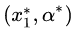
第一种定义:沿着与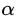
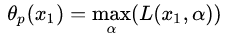

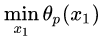
第二种定义:沿着与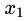
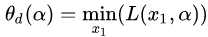
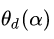
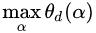
从图8的二维情况思考神秘的四维空间中的拉格朗日函数,
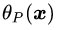
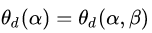
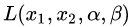
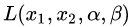
至此,我们比较形象地描述了一个有约束条件下的函数优化问题的拉格朗日对偶问题求解过程以及相应的几何解释。
新人福利
关注 AI 研习社(okweiwu),回复 1 领取
【超过 1000G 神经网络 / AI / 大数据,教程,论文】
零基础学SVM—Support Vector Machine系列之一
▼▼▼