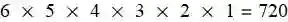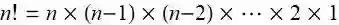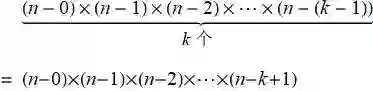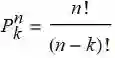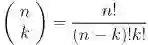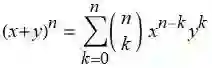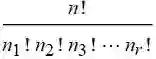【排列组合】- 图解概率 01

01 排列组合

计数基本法则

乘法法则:如果一个试验分成两个阶段, 其中第一阶段 有 m 种可能发生的结果, 第二阶段有 n 种可能发生的结果, 则对这个试验, 一共有 m*n 种可能的结果. 

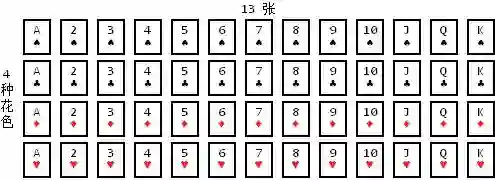
比如, 在一副扑克牌中, 有 4 种花色, 而每种花色又有 13 张, 这里计数就需要乘法法则.

置换(Substitution)

置换: 将 n 个事物按顺序进行排列. 比如, 如果将 3 种小动物排列, 那么共有多少种排法?

如果是 6 种不同动物的话, 置换按照乘法法则计算:

由此可得到下面的结果 720: 

阶乘

这样递减整数相乘称为阶乘(factorial). 因此, 把 n 个事物排列, 共有下面种摆法.

注意: 0! = 1 这里有个[遇见数学]翻译组视频推荐观看《为什么 0! = 1 ?》, 里面给出了好几种解释.

排列(Permutation)

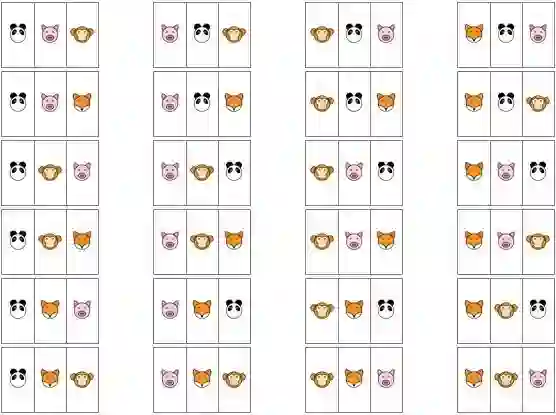
置换是对 n 个事物的所有排列. 如果是从 n 个中取出一部分就称之为排列. 比如将熊猫君, 猪弟, 猴哥, 狐娘取出 3 个进行排列, 所有的排法如下图所示:

注意: 排列与置换都需要考虑顺序. 比如下面 3 种小动物的排法, 因为顺序不同, 所以对于排列与置换而言是不同的排列, 数量为 3!=6 种.

由上面置换的阶乘公式也可以得到求从 n 种事物取出 k 种排列的总数:

也可以用阶乘来表示排列.

组合(Combination)

置换和排列都是考虑顺序的, 而组合不考虑顺序的. 如上面 3 种小动物的排列对于组合而言只计为 1:

考虑计算 4 种动物里取 3 中的组合数, 只需要这样计算就可以.

1. 首先, 考虑顺序按排列那样进行计算;

2. 再来去除掉重复计算的部分;

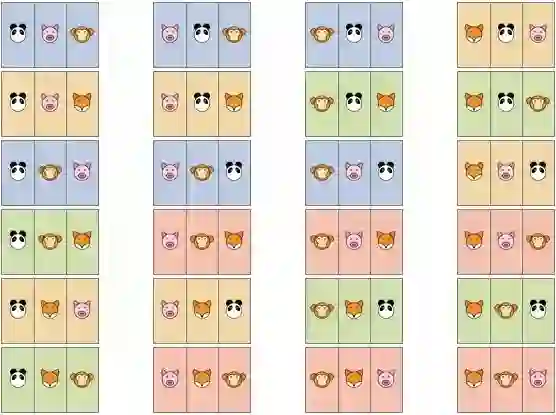
先按第一步进行排列计算, 将熊猫君, 猪弟, 猴哥, 狐娘取出 3 个进行排列, 所有的排法共 4!=24 种, 如下图所示:

请注意上图共有 4 种背景, 每种背景的小动物种类是相同的, 只不过顺序不同. 以浅蓝色背景的熊猫君, 猪弟, 猴哥为例. 如果考虑顺序的话, 共出现 6 边, 也即是 3! . 所以对于组合而言, 要将排列数中除以重复倍数 3!, 即组合数为 4. 下图即为 4 取 3组合结果等于 4:

下式即为计算组合的公式:

二项式定理

从 n 种物品中取 r 种的组合数也称为二项式系数(binomial coefficient), 也是二项式定理中重要的系数部分:

多项式系数

我们还能进一步推广组合公式. 如果为 n 个对象, 其中包括第一组 n1 个对象 , 第二组 n2 个对象, 第三组 n3 个对象.... , 则排列数目计算公式, 称之为多项式系数()multinomial coefficient):

  参考资料:

《程序员的数学》 结城浩

《概率导论》 Dimitri P. Bertsekas, John N. Tsitsiklis