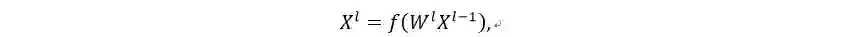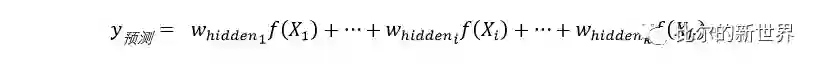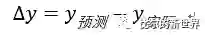纯Python搭建一个深度神经网络并用于房价预测

背景

深度神经网络模型是当前火热的人工智能的基石，深度神经网络模型可以应用于房价预测、股票预测、人脸识别、自动驾驶等各种场景。本文将详细讲解如何使用python从零开始搭建一个神经网络模型，并应用于房价预测。

摘要

1. 房价数据介绍

2. 深度神经网络介绍

3. 神经网络前后向传播计算详解

4. 训练深度神经网络模型并预测房价

5. 总结

 

代码

话不多说，先上代码。人生苦短，我爱python。

https://github.com/hellobilllee/dnn_house_price_prediction_scratch

房价数据介绍

本文将预测波士顿郊区自住房屋价格的中位数。使用波士顿房价(BostonHousePrice)数据集，一部分数据用于训练模型，另一部分数据用于验证模型的效果。数据下载地址：https://archive.ics.uci.edu/ml/machine-learning-databases/housing/

波士顿房价数据说明：此数据源于美国某经济学杂志，用于分析研究波士顿房价，共包含506行，14列。数据集中的每一行对应于影响波士顿某一城镇房价的各种数据，比如犯罪率、当地房产税率等。本数据集信息维度仅用于分析研究，在中国，是否是学区房等信息也是房产价格的重要参考指标。

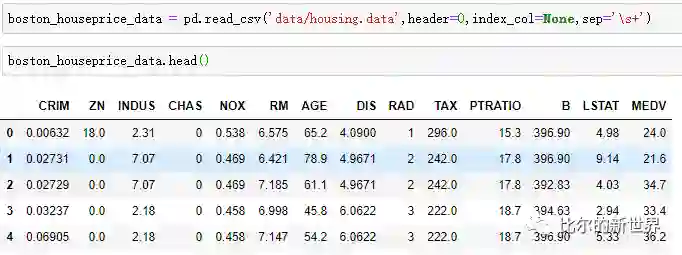
数据示例

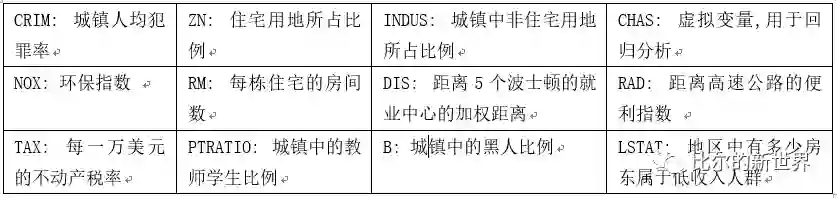
 数据名称解释

本文预测目标为MEDV（自住房屋房价中位数，也就是均价）。假设当前我们的深度神经网络模型已经训练好了，我们将某一城镇住房除需要预测的房屋均价外其它信息输入到网络当中，神经网络会输出一个预测的房屋均价值，可以通过比较预测值与实际值之间的偏差大小来评估神经网络的预测效果。

 

神经网络介绍

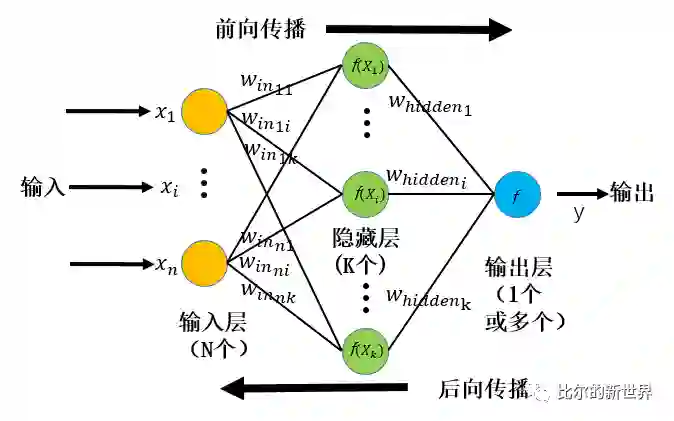
典型神经网络结构

典型的神经网络结构如下图所示，包含输入层、隐藏层（可以有多层）和输出层。每一层当中包含很多存储数据的节点，称之为神经元，每一个神经元都与下一层所有神经元连接，每一对连接都有对应的一个参数。这种连接维持了神经元之间信息的传递，信息的传递其实就是一个数学计算过程。

前向传播过程输入信息由输入层->隐藏层->输出层。

后向传播过程更新信息由输出层->隐藏层->输入层。

预测的时候，输入原始数据信息到输入层，经过中间层的数学计算，得到输出，即房屋均价；训练的时候，先进行前向传输预测得到房屋均价输出，然后根据输出与实际房屋均价的差距，进行后向传播，这个过程会调整网络之中的参数，从而使得下一次预测更为准确。

 

深度神经网络结构

 

前向传播计算公式

前向传播时每一层计算公式：

l 表示第l 层，W表示第l 层的参数矩阵，X表示第l -1 层的输入数据矩阵,f 表 示某类数学函数，也称激活函数。常用激活函数有ReLU, Sigmoid, TanH, Identity。

计算公式展开

假设使用Sigmoid激活函数，则：

输出y的计算为：

本文预测房屋均价，为回归问题，输出使用Identity函数，所以预测值为：

          

假设真实的房价为， 则预测值与真实值的绝对误差（MAE）为：

当然也可以采用别的损失函数来衡量预测与实际值的差别，比如均方误差(MSE)。

后向传播过程就是根据预测值与真实值的差距大小逐层对网络参数进行调整，使得预测值与真实值一致。

网络参数初始化

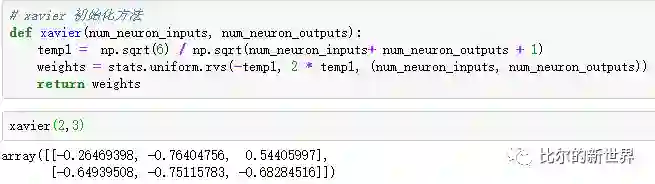
神经网络参数通过后向传播不断优化，使得模型预测值与真实值接近。一开始我们并不知道最优参数值，需要对参数进行随机初始化。对参数进行怎样的随机初始化其实也很有讲究，特别是对于深度神经网络。本文当中，我们使用xavier初始化方法，源自论文“Understanding the difficulty of training deep feedforward neuralnetworks”。假设我们输入层神经元为2，隐藏层神经元为3，则连接这两层之间的参数进行初始化代码如下：

 

前向传播

参数初始化及输入数据到隐藏层

我们已经知道，输入信息在网络当中逐层向前传播并最终得到输出的过程叫做前向传播，每经过一层都会进行一系列数学计算。假设现在我们将数据集当中的第一条信息输入到网络当中，当然，预测目标MEDV不能输入进去。

除去MEDV外，一共还有13个数据，这13个数据将被输入到输入层的13个神经元当中，输入层的神经元个数与输入数据的信息维度一致，我们将输入数据表示为inputs。

接下来，输入层数据将通过输入层与隐藏层之间的连接，通过计算被传播到隐藏层。隐藏层神经元的个数可以自己随意确定，一般比输入层的神经元个数多，通常可以通过经验结合实验进行合理设置。这里我们将第一层隐藏层的神经元个数设置为16个,那么输入层与第一个隐藏层之间的连接个数为13*16=208，这种相邻层之间每一对神经元都有连接的参数层我们称之为全连接层。

我们习惯将数据用矩阵表示，这样方便进行数学计算。比如输入一条数据时，inputs就是一个[1,13]的矩阵，表示长度为1，宽度为13，共保存有1*13=13个数据，而此时第一层全连接层的权重参数为[13,16]的矩阵，表示长度为13，宽度为16，共保存有13*16=208个数据。

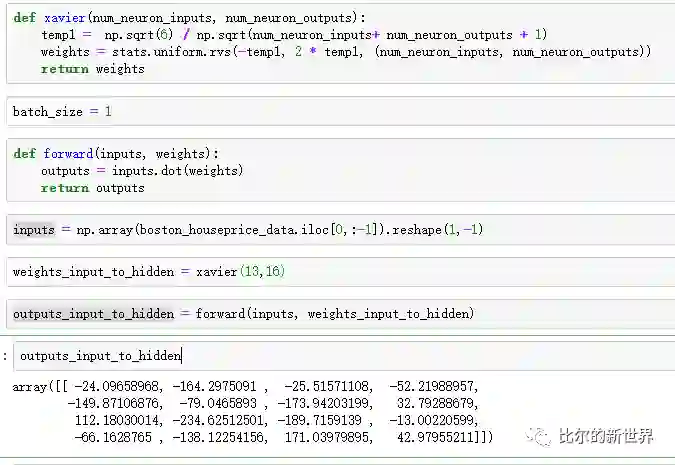
我们可以通过上面的参数初始化函数对参数进行初始化，然后按照前向传播计算公式计算隐藏层神经元的输入。代码如下：

可以看到，通过对输入和连接参数进行计算，我们可以得到一个16维的输出，分别对应于第一个隐藏层16个神经元。将这一步计算好的数据输入第一个隐藏层16个神经元之前，还需要给每一个结果加上一个偏置（bias），即给每一个结果再加上一个随机数，这样做的原因主要是接下来我们需要将输入隐藏层的结果输出到激活函数当中去，而这个随机数有助于调整激活函数在目标参数空间中左右移动，使得神经网络有更大的灵活性和更强的学习能力。我们可以给inputs增加一维恒为1的数据，然后在全连接参数层输入端多添加一个权重参数达到同样的目的。在文字稿中，我们并不引入bias数据，但是在实际训练的代码当中会加入进去。batch_size表示我们一次性输入到网络的数据条数，比如我们现在是一条一条输入，那么batch_size就等于1.

隐藏层输入数据过激活函数

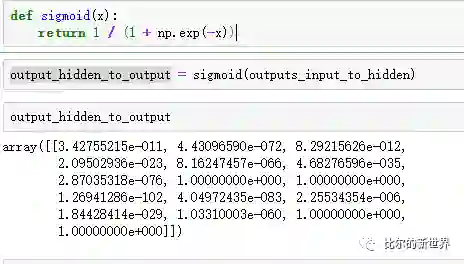
现在我们得到了第一个隐藏层的输入数据，接下来我们需要将该层每一个神经元的数据输入到激活函数得到隐藏层的输出。这里我们使用sigmoid激活函数，代码如下：

 

隐藏层输出数据至输出层

接下去需要将第一个隐藏层的输出数据进一步往前传播。隐藏层可以有多个，这里我们只使用一个隐藏层。每一层的操作过程和上面的基本一样，都是：

“上层输出矩阵乘当前全连接层参数->加偏置->输入激活函数->输出“

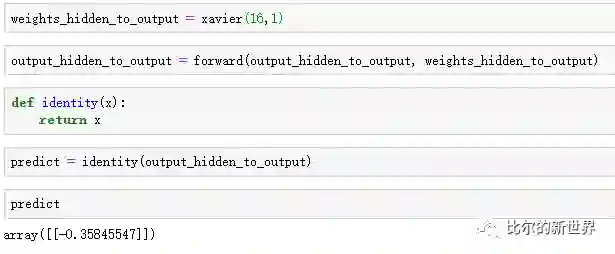
输出层的激活函数使用Identity函数，其实这里不应该叫激活函数了，叫输出转换函数更合适，但是这样可以将输出层看成和隐层一样，更方便理解。通常进行连续值的预估的时候，输出层使用Identity函数（其实就是线性函数，且是原样输出那种），而进行离散值的预估的时候，输出层使用Sigmoid函数。所谓连续值，比如房价，是在一个连续的范围内波动的；而离散值，比如识别一张图片里面是猫还是狗，就只需要区分出有限的值即可。

隐藏层的数据继续传播到输出层的代码如下：

 

可以看出，结果为负值，与实际值（24.0）相差十万八千里。这是因为网络还没有通过后向传播调整连接网络层之间的参数值，通过不断地输入样本进行反复学习和更新网络参数，强化神经网络地预测能力。接下来，我们将继续通过代码学习神经网络后向传播。

 

后向传播

 

在网络未学习之前，是没有预测能力的，比如上面我们通过前向传播预测的结果与实际值相差甚远。所谓神经网络的学习，其实就是不断地调整连接各个网络层的参数，使得最终计算结果能够与实际值一致或者接近。整个调整过程，被称为后向传播。

首先我们需要计算出预估值与实际值之间的差距，这个差距是网络层中的所有参数一起造成的，但是每一个参数对这个错误的影响是不一样的，所以我们要根据某种规则来调整每一个参数，常用的调整规则称为梯度下降算法（GD，Gradient Decent）。

我们根据预测误差大小调整最后一个全连接层之间的参数，然后根据该层的输入和后向传播的误差，逐层往前调整参数。我们可以每过一条数据就更新一次参数，也可以过几条数据后通过累计误差来更新一次参数，也可以在训练数据集中随机选择一些数据而不是所有数据来训练，上面的方法依次被称为梯度下降、批量梯度下降、随机梯度下降。

 

计算预估误差

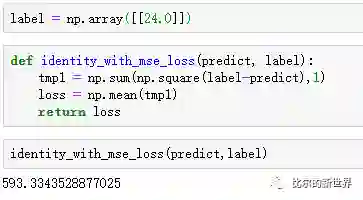
我们首先计算预估值与实际值之间的差距，本文中使用均方误差来衡量这种差距：

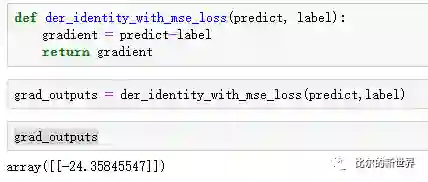
然后我们计算输出层神经元输出值需要调整的大小：

 

可以看到这样调整后预测结果就应该等于真实值，但是我们的步子一下不能迈这么大，因为当输入下一条不同的样本，这么调整预测效果可能就不好，所以后面调整的时候我们会有一个所谓学习率（lr, learning rate）的参数，这个参数控制权重调整的幅度。使用均方误差做损失函数来衡量误差，其梯度为2*（predict-label），常数项2通常省略，可以理解为将学习率调小了两倍。

 

调整第二个参数层参数

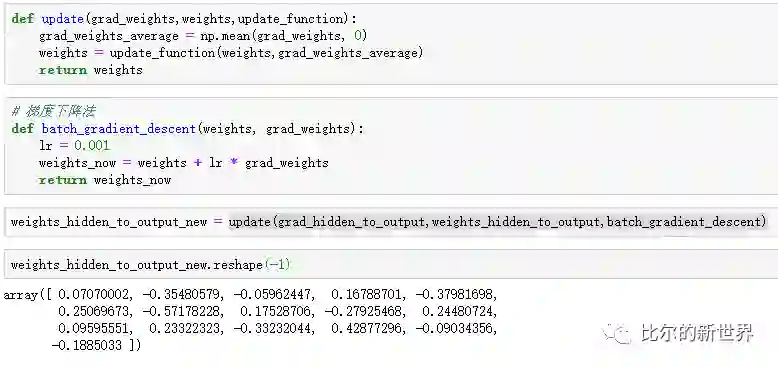
接下来我们计算连接隐藏层与输出层的全连接层参数需要调整的大小。由于输出层神经元的输出值等于其输入值，而其输入值由隐藏层的输出与参数共同决定，所以该全连接层参数大小的调整，需要参考隐藏层输出值大小，其实就是与对应的输出值的大小成正比：

 

接下来我们可以开始调整该全连接层参数（使用reshape是为了节约展示空间，实际中不用），我们使用了最简单的梯度下降算法，学习率lr=0.001：

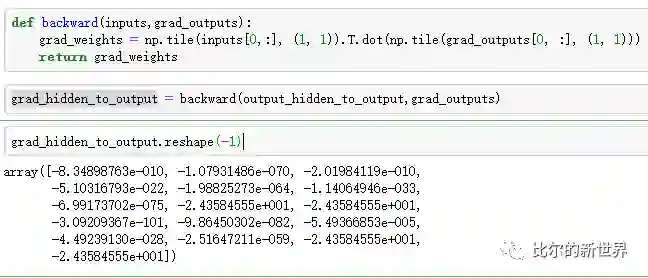
计算隐藏层激活函数输入输出梯度

现在连接隐藏层与输出层的参数调整了一次，接下来还需要调整连接输入层和隐藏层的参数。但是隐藏层输出前还经过了一个sigmoid激活函数，所以这里需要计算经过sigmoid函数前后隐藏层需要调整的梯度大小。

首先计算经过sigmoid后需要调整的梯度，这里直接将输出层需要调整的梯度点乘该全连接层的参数即可：

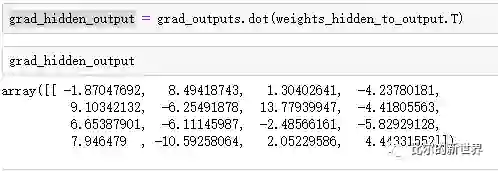
然后计算经过sigmoid前需要调整的梯度，这里需要求sigmoid函数的导数：

 

调整第一个参数层的参数

现在可以开始更新连接输入层和隐藏层之间的参数了，计算过程和更新隐藏层和输出层之间的参数一样。

现在我们已经通过输入一条数据，前向传播做预测，根据预估误差做后向传播，调整了一次连接各网络层的参数。我们不断地输入数据，反复地更新网络参数，直到误差足够小，或者我们觉得学习时间够了，那么我们的神经网络模型就算学好了。

我们将学习好的网络参数保存下来，通过输入新数据，即神经网络从来没有见过的数据，测试神经网络的预测能力。

接下来我们就通过波士顿房价(Boston HousePrice)数据集，将前4/5的数据用于训练，后1/5数据用作测试，来看看神经网络的学习能力和预测能力。

 

训练深度神经网络模型并预测房价

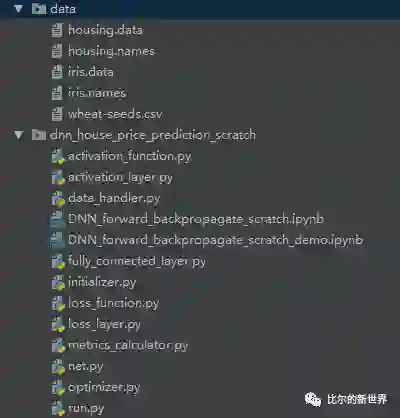
整个项目结构如下图所示，包含一个数据目录和代码目录。代码目录包含激活函数（层），数据处理，全连接层，初始化，损失函数（层），评估指标计算，网络搭建，梯度优化器这几个模块：

首先我们导入一些数据处理和画图所需要的包：

然后我们读取数据，打印数据大小，查看数据示例：

然后将待预测的数据标签与辅助训练的数据信息分开，最后一列为待预测房价数据标签：

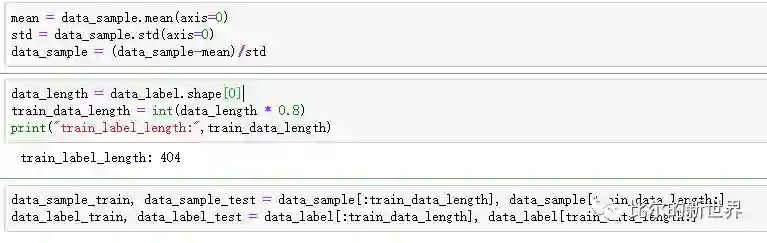
对数据进行减均值除方差的标准化处理，这样做有助于神经网络的收敛（学习），然后使用4/5的数据做训练数据，剩下的1/5数据做测试数据：

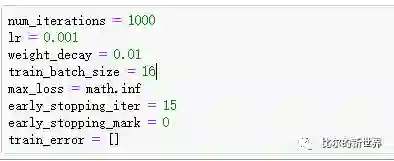
定义一些神经网络的参数，如迭代次数（num_iterations,学习次数），学习率（lr, 调节参数更新幅度），一次学习的数据大小（train_batch_size），还有一些早停参数（防止学习过猛）， train_error用于记录每次学习误差：

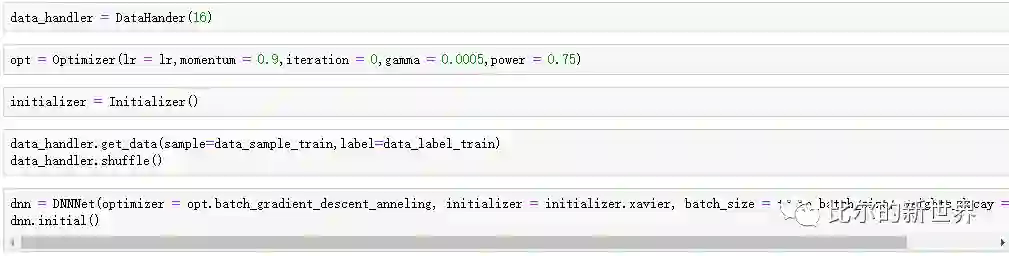
然后可以使用数据处理模块（DataHander），优化器模块(Optimizer)，数据初始化模块（Initializer），网络搭建模块（DNNnet），批量读取数据并搭建深度神经网络：

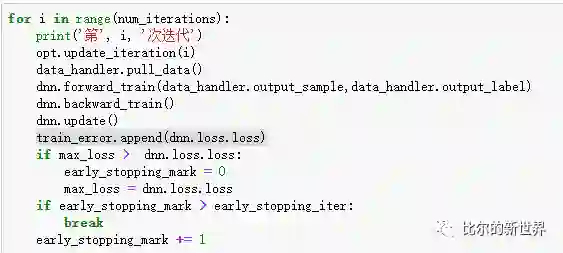
接下来可以开始训练了，每次拉取一批数据data_handler.pull_data()，然后进行前向传播dnn.forward_train()，后向传播dnn.backward_train()，更新参数dnn.update()，记录训练误差train_error.append(dnn.loss.loss)，这个过程反复很多次，直到训练误差连续15次都没有降低（ 通过early_stopping_iter参数进行设置）：

我们可以看到，第一次训练，神经网络的预测值跟真实值完全不搭边，但是训练到第71次的时候，预测值与真实值已经很接近了：

 

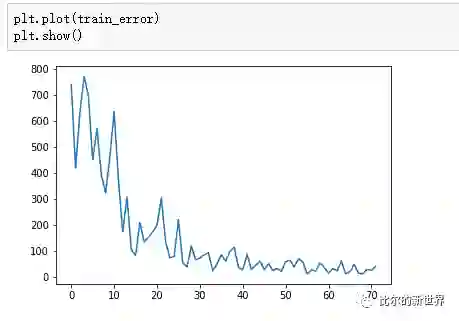
我们可以来看一下随着训练次数增加训练误差的变化趋势图。可以看到训练误差是在不断减小的，但是当中在不断的波动，这是因为我们的数据集比较小，而我们使用的batch_size也比较小，如果不同样本间差异比较大的话，很容易出现这种波动，同时训练学习率影响也非常大：

 

总结

本文我们简单介绍了一下神经网络的定义，神经网络怎么做前向传播得到输出，怎么做后向传播更新网络参数，然后使用python从零开始搭建了一个深度神经网络模型，并用于房价预测。可以看到，深度神经网络模型在训练前预测能力基本没有，训练后预测能力急剧提升，可见神经网络强大的学习能力。如何进一步提升神经网络的预测能力？大家可以试试调节网络参数，网络结构，优化方法等。水平有限，如有疑问或者建议，欢迎留言交流。代码免费开源给大家，如果各位爷觉得哎哟不错是干货，那就点个在看或关注支持一下吧。

代码地址：下载后直接运行run.py即可得到上图训练曲线

https://github.com/hellobilllee/dnn_house_price_prediction_scratch

---

由于微信平台算法改版，公号内容将不再以时间排序展示，如果大家想第一时间看到我们的推送，强烈建议星标我们和给我们多点点【在看】。星标具体步骤为：

（1）点击页面最上方"AINLP"，进入公众号主页。

（2）点击右上角的小点点，在弹出页面点击“设为星标”，就可以啦。

感谢支持，比心。

欢迎加入AINLP技术交流群

进群请添加AINLP小助手微信 AINLPer（id: ainlper)，备注NLP技术交流

推荐阅读

这个NLP工具，玩得根本停不下来

征稿启示| 200元稿费+5000DBC（价值20个小时GPU算力）

完结撒花！李宏毅老师深度学习与人类语言处理课程视频及课件（附下载）

从数据到模型，你可能需要1篇详实的pytorch踩坑指南

如何让Bert在finetune小数据集时更“稳”一点

模型压缩实践系列之——bert-of-theseus，一个非常亲民的bert压缩方法

文本自动摘要任务的“不完全”心得总结番外篇——submodular函数优化

Node2Vec 论文+代码笔记

模型压缩实践收尾篇——模型蒸馏以及其他一些技巧实践小结

中文命名实体识别工具（NER）哪家强？

学自然语言处理，其实更应该学好英语

斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLPer(id：ainlper)，备注工作/研究方向+加群目的。

阅读至此了，分享、点赞、在看三选一吧🙏