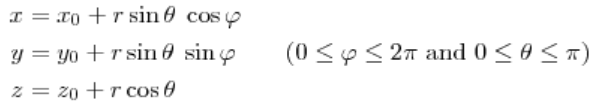没有完整图时，如何使用图深度学习？你需要了解流形学习2.0版本

机器之心编译

编辑：陈萍

流形学习，自 2000 年在著名的科学杂志《Science》被首次提出以来，已成为信息科学领域的研究热点。可能很多人会问，流形学习有什么用呢？首先流形学习可以作为一种数据降维的方式，第二，流形能够刻画数据的本质。其主要代表方法有等距映射、局部线性嵌入等。那么，具有流形学习 2.0 之称的潜图学习方法如何呢？

自从神经网络提出以来，其在人脸识别、语音识别等方面表现出卓越的性能。以前需要人工提取特征的机器学习任务，现在通过端到端的方法就能解决。

传统的深度学习方法在提取欧氏空间数据（比如图片是规则的正方形栅格，语音数据是一维序列）的特征方面取得了巨大的成功。但是，在许多任务中，数据不具备规则的空间结构，即非欧氏空间下的数据，如电子交易、推荐系统等抽象出来的图谱，图谱中每个节点与其他节点的连接不是固定的。在经典的 CNN、RNN 等框架无法解决或效果不好的情况下，图神经网络应运而生。

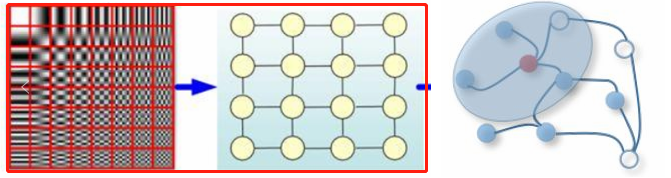
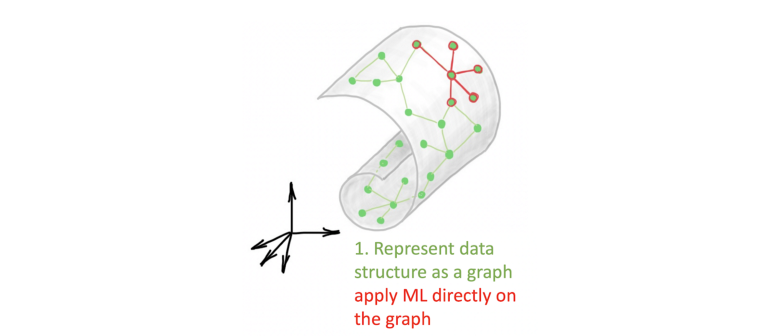
图左（红框）：欧氏空间数据；图右：非欧氏空间数据。

图神经网络利用关系归纳偏置来处理以图形式出现的数据。然而，在许多情况下，并没有现成的图。那么图深度学习适用于这类情形吗？本文将介绍潜图学习（latent graph learning）和更早的流形学习（manifold learning）。

潜图学习

在过去的几年里，人们对使用机器学习方法处理图结构数据产生了浓厚的兴趣。这类数据自然也出现在许多应用中，例如社会科学（如 Twitter 或 Facebook 上的用户 Follow 图）、化学（分子可被建模为键连接的原子图）或生物学（不同生物分子之间的相互作用通常被建模为相互作用组图）。图神经网络（GNN）是一种特别流行的图学习方法，该算法通过在相邻节点之间交换信息的共享参数进行局部操作。

然而，在某些情况下，没有现成的图可以作为输入。在生物学中尤其如此，诸如蛋白质 - 蛋白质相互作用的图只有部分已知，因为发现蛋白质相互作用的实验费用昂贵，而且噪声很大。 因此，研究者从数据中推断出图并在其上应用 GNN，并将其称为「潜图学习」。 潜图学习特定于应用，并针对下游任务进行了优化。此外，有时这样的图可能比任务本身更重要，因为它可以传达关于数据的重要洞察，并提供解释结果的方法。

潜图学习是学习具有空边集的图。在这一设置中，输入为高维特征空间中的点云。在集合上进行深度学习的方法（如 PointNet）对每个点应用共享可学习 point-wise 函数，与之不同，潜图学习还寻求跨点信息传递。

DGCNN

点云动态图卷积神经网络（DGCNN）是第一个这样的架构，该架构由麻省理工学院的 Yue Wang 开发。受计算机图形学中涉及 3D 点云分析问题的启发，该架构将图用作点云下局部光滑流形结构的粗略表示。Yue 的一个重要发现是，图在整个神经网络中不需要保持不变，事实上，它可以而且应该动态更新——因此该方法被命名为 DGCNN。

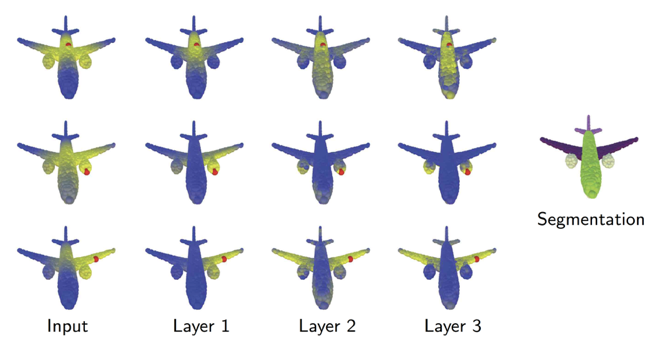
DGCNN 动态构造一个用于特征扩散的 k 近邻图。图依赖于任务，并在每个层之后更新。这幅图（摘自 [4]）展示了与红点的距离（黄色代表更近的点），表明在分割任务中，更深层次的图捕捉语义关系而不是几何关系，如成对的机翼、发动机等。

DGM

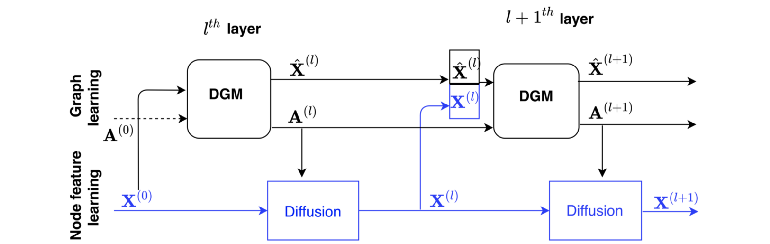
DGCNN 的一个局限性是用相同的空间来构造图和图上的特征。Anees Kazi 和 Luca Cosmo 提出了一种新的架构——可微图模块（DGM），通过对图和特征构造进行解耦来扩展 DGCNN，如下图所示：

DGM 提供了一种基于输入数据构造图并在图上扩散特征的机制。（图源：[5]）

当应用于医学领域问题时，DGM 显示出优秀的结果，例如根据脑成像数据预测疾病。在这些任务中，研究者获取到多个患者的电子健康记录，包括人口统计学特征（如年龄、性别等）和大脑成像特征，并尝试预测患者是否患有神经系统疾病。之前的工作展示了 GNN 在这类任务中的应用，方法是在一个根据人口统计学特征手工构建的「病人图」上进行特征扩散。而 DGM 提供了学习图的优势，可以传达某些特征在特定诊断任务中是如何相互依赖的。其次，DGM 在点云分类任务中也击败了 DGCNN，不过优势很小。

流形学习

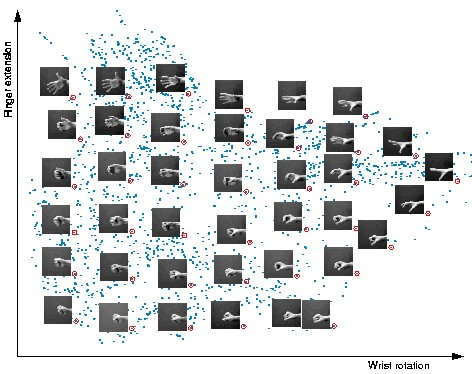
DGCNN 和 DGM 在概念上与流形学习或非线性降维算法相似，流形学习很早就已出现并流行，且目前仍用于数据可视化。流形学习方法的基本假设是数据具有内在的低维结构。虽然数据可以在数百甚至数千维的空间中表示，但它却只有几个自由度，示例如下：

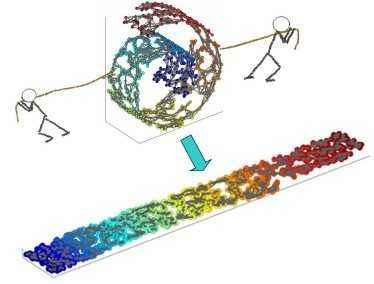
虽然这个数据集中的手部图像是高维的（64x64 像素构成 4096 个维度），但它们本质上是低维的，可以用两个自由度来解释：手腕旋转和手指伸展。流形学习算法能够捕捉数据集的这种内在低维结构，并将其在欧几里德空间中进行表示。（图源 [9]）

再比如球面上的一点（即三维欧式空间上的点），可以用三元组来表示其坐标：

但事实上这个三维坐标只有两个变量 θ 和 φ，也可以说它的自由度为 2，正好对应了它是一个二维的流形。

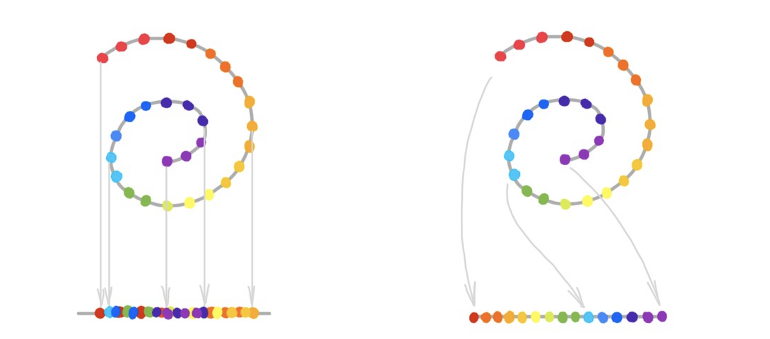
流形学习的目的是捕捉这些自由度，并将数据的维数降至其固有维数。 流形学习与 PCA 等线性降维方法的重要区别在于，由于数据的非欧几里德结构，我们可能无法通过线性投影恢复流形。如下图所示，线性降维（左）为线性降维，流形学习（右）为非线性降维。

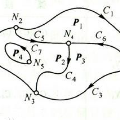
流形学习算法在恢复「流形」方法上各不相同，但它们有一个共同的蓝图。

首先，创建一个数据表示，通过构造一个 k 近邻图来获取其局部结构。其次，计算数据的低维表示（嵌入），并试图保留原始数据的结构。这是大多数流形学习方法的区别所在。这种新的表示将原来的非欧几里德结构「展平」成一个更容易处理的欧几里德空间。第三，一旦计算出表示，就会对其应用机器学习算法（通常是聚类）。

多种流形学习方法的蓝图：首先，将数据表示为图；其次，计算该图的低维嵌入；第三，将 ML 算法应用于这种低维表示。

这其中面临的一项挑战是图构建与 ML 算法的分离，有时需要精确的参数调整（例如邻域数或邻域半径），以确定如何构建图才能使下游任务正常运行。流形学习算法更严重的缺点或许是：数据很少表示为低维的原始形式。例如，在处理图像时，必须使用各种人工制定的特征提取技术作为预处理步骤。

图深度学习提供了一种现代方法，即用单个图神经网络代替上文提到的三个阶段。例如，在 DGCNN 或 DGM 中，图的构造和学习是同一架构的一部分：

潜图学习可以看作是流形学习问题的一种现代设置，在这里，图被学习并用作某些下游任务优化的端到端 GNN pipeline 的一部分。

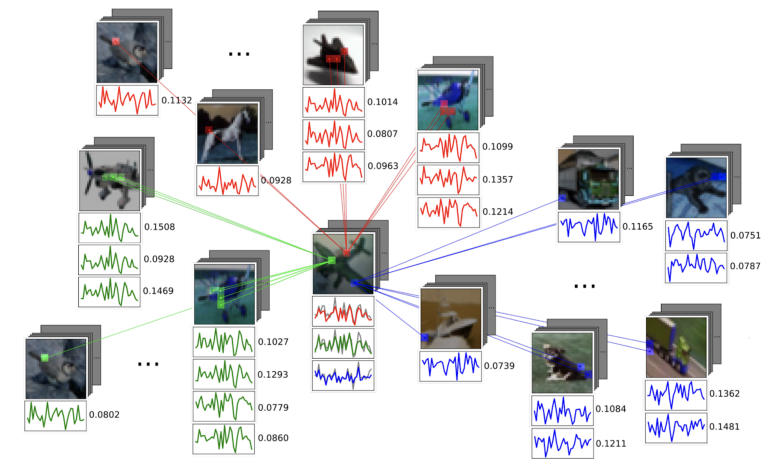
这种方法的吸引力在于：将单个数据点和它们所在的空间结合在相同的 pipeline 中。在图像的例子中，我们可以使用传统的 CNN 从每个图像中提取视觉特征，并使用 GNN 来建模它们之间的关系。

PeerNet 是标准 CNN 中基于图的正则化层，可聚合来自多个图像的相似像素，从而降低对对抗性扰动的敏感性。（图源 [12]）

潜图学习的其它应用

潜图学习还有许多其他有趣的应用。

• 第一是少样本学习：利用基于图的方法从少量样本中进行归纳（重点：只需要少量带有标注的样本）。在计算机视觉中，数据标注量从几千到上万不等，成本很高，因此少样本学习变得越来越重要。

• 第二是生物学领域：人们经常通过实验观察生物分子如蛋白质的表达水平，并试图重建它们的相互作用和信号网络。

• 第三是对物理系统的分析：其中图可以描述多个对象之间的交互作用。尤其是处理复杂粒子相互作用的物理学家，最近对基于图的方法表现出了浓厚的兴趣。

• 第四是 NLP 问题：在 NLP 领域中，图神经网络可以看作是 transformer 架构的泛化。所提到的许多问题也提出了在图结构中加入先验知识，这一结构在很大程度上仍然是开放的：例如，人们可能希望强迫图遵守某些构造规则或与某些统计模型兼容。

潜图学习，虽然不是全新的领域，但它为旧问题提供了新的视角。对于图机器学习问题而言，这无疑是一个有趣的设置，为 GNN 研究人员提供了新的方向。

参考链接：

https://towardsdatascience.com/manifold-learning-2-99a25eeb677d

https://zhuanlan.zhihu.com/p/75307407?from_voters_page=true

从算法到应用，入门声纹技术。

10月19日，第一讲：音频基础与声纹识别。谷歌资深软件工程师、声纹识别与语言识别团队负责人王泉老师将介绍声纹识别技术相关基础知识，包括发展历程、听觉感知和音频处理相关基本概念与方法、声纹领域最核心的应用声纹识别等。

添加机器之心小助手（syncedai5），备注「声纹」，进群一起看直播。

© THE END 

转载请联系本公众号获得授权

投稿或寻求报道：content@jiqizhixin.com