在稀疏和欠明确奖励中学习泛化
文 / Rishabh Agarwal,Google AI 定向实习生;Mohammad Norouzi,研究员
强化学习 (RL) 为优化目标导向行为提供了一个灵活而统一的框架,并助力研究者在解决玩视频游戏、连续控制和 机器人学习 等具有挑战性的任务方面取得了显著成功。RL 算法在这些应用领域的成功往往取决于高质量密集奖励反馈的可用程度。但是,将 RL 算法的应用范围扩展到含有稀疏和欠明确奖励的环境中,这是一项持续性挑战,需要学习型智能体根据有限的反馈学习泛化(即学习正确的行为)。在这类问题设置中研究 RL 算法的性能时,一个很自然的方法是借助语言理解任务。在此类任务中,智能体需要在接收自然语言输入后生成复杂响应,以实现输入中指定的目标,同时只接收二进制的成功 / 失败反馈。
例如,我们假设一个 “盲” 智能体,它的任务是通过遵循一系列自然语言命令(例如,“右、上、上、右”)到达迷宫中的目标位置。在给定输入文本后,智能体(绿色圆圈)需要解释命令,然后根据解释采取行动,以生成动作序列 (a)。如果到达目标位置(红色星标),智能体会获得显示为 1 的奖励,否则将得到 0。由于此智能体无法访问任何视觉信息,因此,要完成该任务并泛化至新指令,唯一的方法就是正确解释指令。
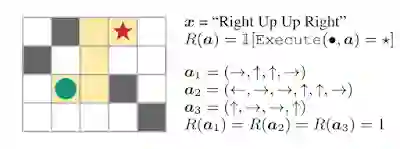
在这个指令跟随任务中,行动轨迹 a1、a2 和 a3 均到达目标位置,但 a2 和 a3 序列没有遵循指令。这阐释的是欠明确奖励的问题
在这类任务中,RL 智能体需要从稀疏(只有很少的轨迹产生了非零奖励)和欠明确(没有区分有意的成功和偶然的成功)奖励中学习泛化。重要的是,由于欠明确奖励,智能体可能会收到鼓励其在环境中利用伪模式的正反馈。这可能会引发奖励式黑客行为,导致在实际系统中部署时出现意外和有害的行为。
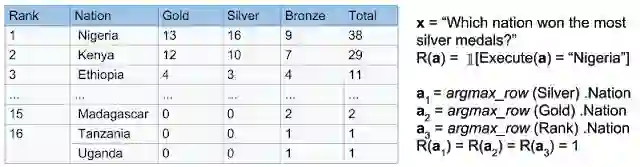
在《从稀疏和欠明确奖励中学习泛化》(Learning to Generalize from Sparse and Underspecified Rewards) 一文中,我们提出通过开发元奖励学习 (MeRL) 来解决欠明确奖励的问题,元奖励学习可以通过优化辅助奖励函数为智能体提供更精确的反馈。MeRL 与内存缓冲区中使用探索策略收集的成功轨迹相结合,以便从稀疏奖励中学习。此方法的有效性在语义分析中得到了证明,语义分析的目标是学习从自然语言到逻辑形式的映射(例如,将问题映射到结构化查询语言 (SQL) 程序中)。在论文中,我们研究了弱监督问题的设置,其目标是在没有任何形式的程序监督的情况下,从问答对中自动发现逻辑程序。例如,给出问题 “哪个国家赢得的银牌最多?” 和一个相关的 Wikipedia 表格,智能体需要生成一个类似 SQL 的程序,并由该程序给出正确答案(即 “尼日利亚”)。
注:Wikipedia 表格 链接
https://en.wikipedia.org/wiki/Athletics_at_the_1991_All-Africa_Games#Medal_table
我们提出的这一方法在 WikiTableQuestions 和 WikiSQL 基准测试中获得了最优结果,将此前的结果分别提高了 1.2% 和 2.4%。MeRL 可以自动学习辅助奖励函数,不需要使用任何专业演示(例如,实际 程序),这使它的适用范围更加广泛,而且有别于以前的奖励学习方法。下图描绘了此方法的总体概览:
注:WikiTableQuestions 链接
https://nlp.stanford.edu/blog/wikitablequestions-a-complex-real-world-question-understanding-dataset/
WikiSQL 链接
https://github.com/salesforce/WikiSQL
实际 链接
https://en.wikipedia.org/wiki/Ground_truth
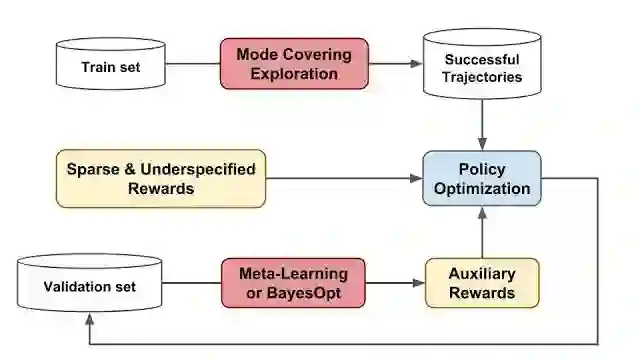
我们所提方法的概览。我们采用 (1) 涵盖探索模式,在内存缓冲区收集了一组多样化的成功轨迹;(2) 元学习或贝叶斯优化,学习能够为策略优化提供更精确反馈的辅助奖励
元奖励学习 (MeRL)
MeRL 在处理欠明确奖励时获得的关键发现是,偶然成功的虚假轨迹和程序会损害智能体的泛化性能。例如,智能体或许能解决上述迷宫问题的某一特定实例。但是,如果它在训练期间学会了执行虚假操作,则在收到没有见过的指令时,很可能就会失败。为了缓解这一问题,MeRL 优化了一个更精确的辅助奖励函数,该函数可以根据行动轨迹的特点区分智能体的成功是有意还是偶然。我们通过元学习,将训练后的智能体在保留验证集上的表现最大化,从而优化辅助奖励。
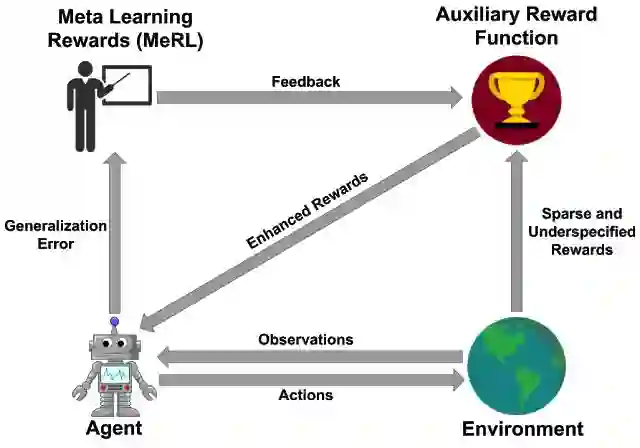
MeRL 示意图:通过从辅助奖励模型中获得的奖励信号来训练 RL 智能体,同时使用智能体的泛化误差来训练辅助奖励
从稀疏奖励中学习
要从稀疏奖励中学习,有效的探索对于寻找一系列成功轨迹而言至关重要。在 论文 中,我们利用 Kullback–Leibler (KL) 散度的 两个方向 来解决这一挑战,KL 散度是两种概率分布差异程度的衡量指标。在下面的示例中,我们使用 KL 散度来最小化固定双峰(紫色阴影)和学习后高斯(绿色阴影)分布之间的差异,这可以分别代表智能体的最优策略和学习后策略的分布。KL 对象的一个方向学习一个分布,该分布试图涵盖这两种模式,而其他对象学习的分布都寻求某种特定模式(即它对某个模式的偏好胜过另一个)。我们的方法利用包含 KL 集中于多个峰值这一倾向的模式来收集多元化的成功轨迹,并利用在轨迹间寻找 KL 隐含偏好的模式来学习稳健的策略。
注:论文 链接、
https://arxiv.org/abs/1902.07198
两个方向 链接
https://wiseodd.github.io/techblog/2016/12/21/forward-reverse-kl/
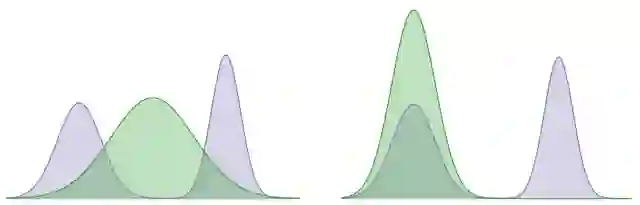
左图:涵盖 KL 的优化模式。右图:搜寻 KL 的优化模式
结论
要将 RL 用于实际应用,设计区分最优和次优行为的奖励函数至关重要。此项研究让我们朝向在没有人为监督的情况下进行奖励函数建模的方向迈出了一小步。在今后的工作中,我们希望从自动学习密集奖励函数的角度来解决 RL 中的信度分配问题。
致谢
此研究系与 Chen Liang 和 Dale Schuurmans 合作完成。感谢 Chelsea Finn 和 Kelvin Guu 对论文进行审校。
更多 AI 相关阅读:


