从Bengio演讲发散开来：探讨逻辑推理与机器学习

机器之心分析师网络

作者：仵冀颖

编辑：Joni

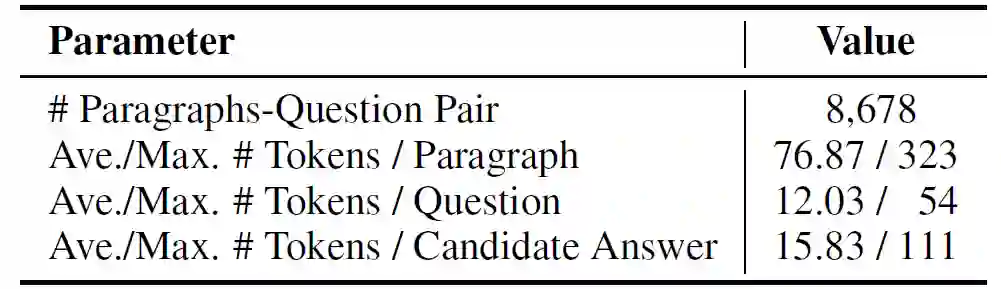
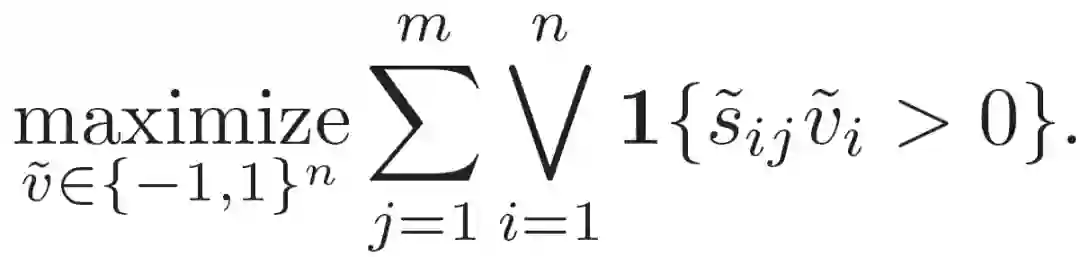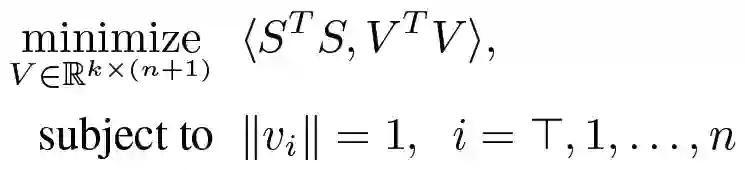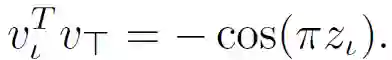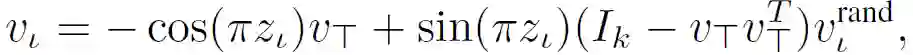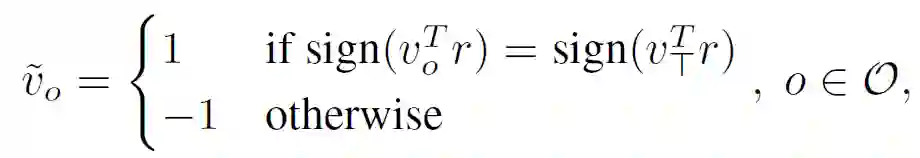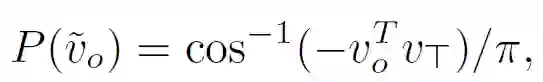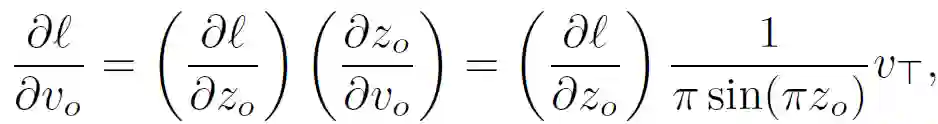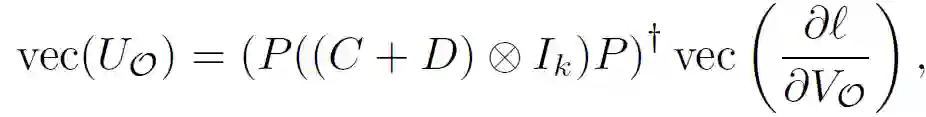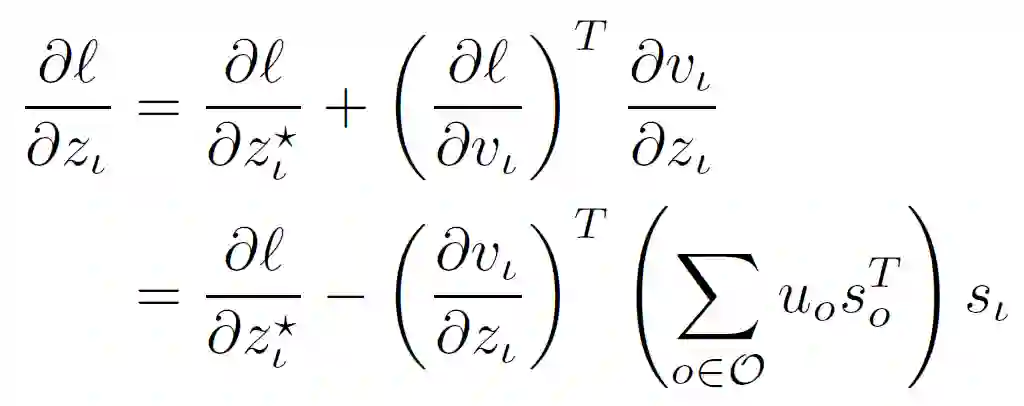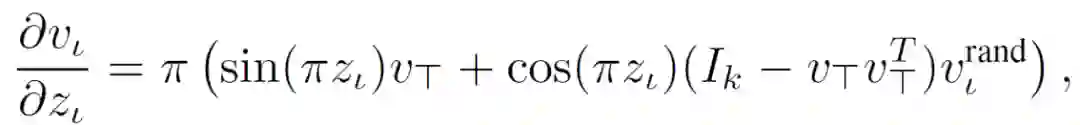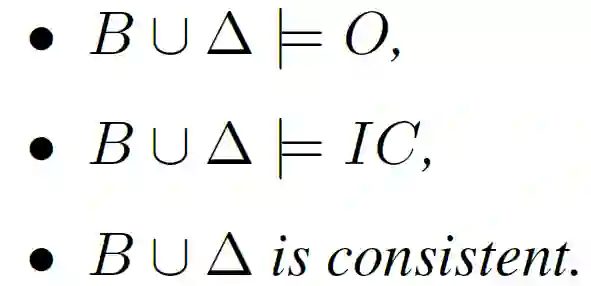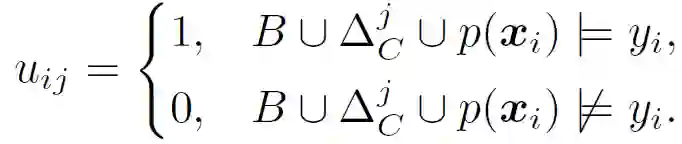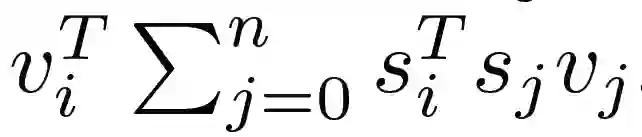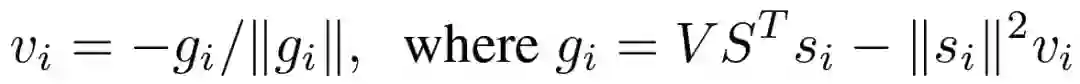Bengio 认为，未来的深度神经网络应当能够实现 System2（逻辑分析系统），实现的是有意识的、有逻辑的、有规划的、可推理以及可以语言表达的系统。本文所讨论的 Logical Reasoning（逻辑推理）拟实现的就是 System2 中重点关注的有逻辑的（Logical）和可推理的（Reasoning）特点。

近年来，深度神经网络的应用获得了巨大的成功，也推动了人工智能的飞速发展。然而，深度神经网络仍存在一些局限性。一般来说，深度神经网络如何进行学习、使用何种算法实现的智能、基于哪些理论分析得出的相关结论并不会在网络架构中有任何的显式或符号表示。也就是说，深度神经网络学习的算法隐式地存储在成千上万甚至是数百万的权重中，这些通常是人类智能体无法破译或验证的。

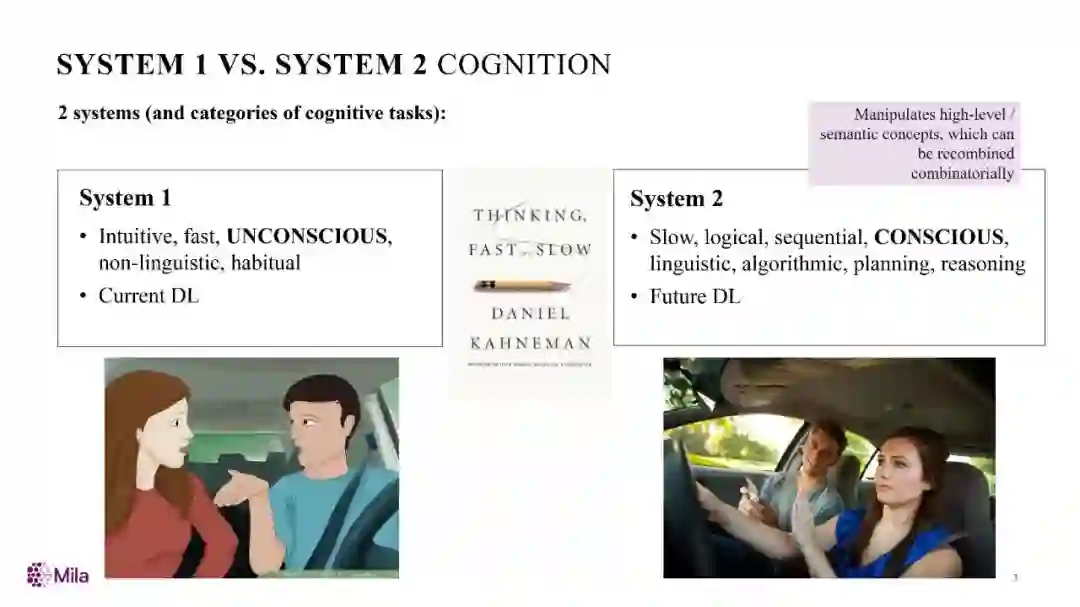
Bengio 在 AAAI 2020 的演讲报告中提出， 人的认知系统包含两个子系统 ：System1（直觉系统），实现的是快速、无意识、非语言的认知，这也是现有的深度神经网络所实现的。他认为，未来的深度神经网络应当能够实现 System2（逻辑分析系统），实现的是有意识的、有逻辑的、有规划的、可推理以及可以语言表达的系统。我们这篇文章中所讨论的 Logical Reasoning（逻辑推理）拟实现的就是 System2 中重点关注的有逻辑的（Logical）和可推理的（Reasoning）特点。

本图选自 Bengio 在 AAAI 2020 的演讲报告

逻辑推理是一个非常宽泛的概念。实际上，我们所熟悉的字符识别、语音识别、图像识别也可以看做是一种逻辑推理，这不过，这些逻辑推理是低层次的，已经能够使用传统的深度神经网络所解决。我们在这篇文章中所讨论的逻辑推理是更高层次的推理过程，即，即使是人来完成这个逻辑推理任务也是要进行一下思考的。

1. 什么是逻辑？

1.1 逻辑的概念

首先，我们来回顾一下什么是逻辑以及什么是 AI/ML 中的逻辑。所谓逻辑，指的是符号化的、基于知识的、推理和其他类似的人工智能方法。基于逻辑的 AI 系统可以被认为是高级编程系统，可以很容易地以紧凑（compact）和可用的（usable）方式编码人类知识。

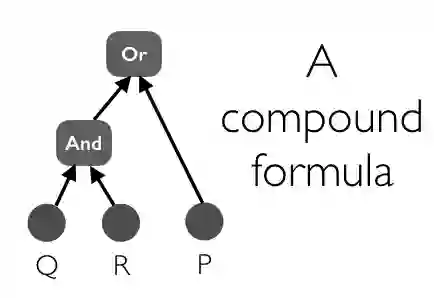
最简单的逻辑系统是命题逻辑（有时称为零阶逻辑）。在命题逻辑中，使用一些被称为句子或公式的对象来编码信息。这些对象代表着对世界的一些陈述。通常，可以使用一些基本语句作为这样的对象。例如，使用「P，Q，R，S…」来表示基本语句，P 可能代表「正在下雨」，是一个原子（Atom）。

可以继续将原子与逻辑连接词如「and，or，if then」等组合形成更多的句子，称为复合公式（Compound Formula）。

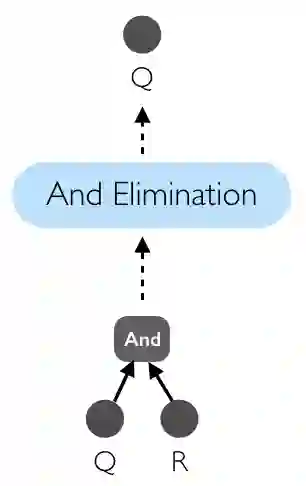
复合公式提供了一种有效的信息表示方法。那么，我们如何利用这些复合公式从已有的信息推断得到新的信息呢？一般可以通过推理（Reasoning）或推论（Inference）来做到这一点。命题逻辑配有一套称为推理方法的方案。推理方法可以被认为是一个小程序，它以一组句子作为输入，并输出一个或多个句子。推论方法也可以被认为是一个小程序，它也以一组句子作为输入，并输出一个或多个句子。下图展示了一种非常直接的推论方法，它接受表示「Q 和 R」的公式，并将公式 R 作为输出。例如，如果输入为「It is sunny, and It is warm」，则输出将为「It is sunny」。

所有的逻辑都配备了一套与上述过程类似的推论方法。逻辑的这些原始内置方法的作用类似于编程语言中的标准库。有了这些方法，就可以将它们组合起来以得到更复杂的方法。

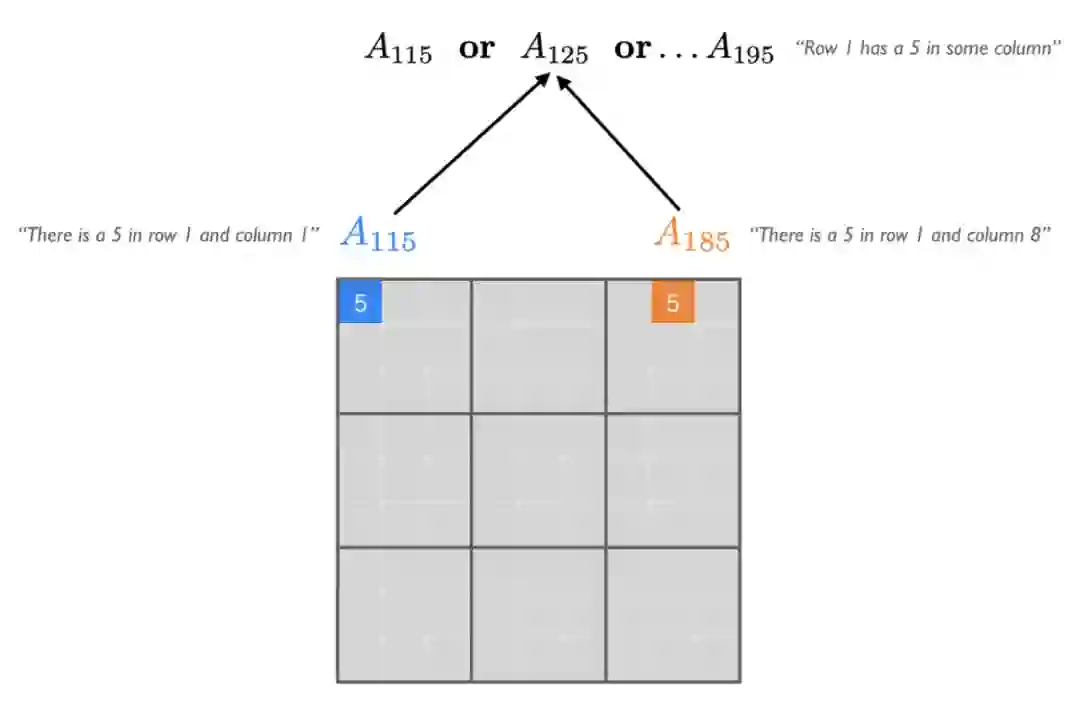
从教学的角度来看，从命题逻辑出发进行介绍是一个很好的起点。但是，对于实际中具有大量对象的领域建模来说，使用命题逻辑是很难处理的。例如，假设我们要写下数独游戏应该满足的约束条件。对于每个数 k，每行 i 和列 j 都对应一个原子 A_ijk，它代表「行 i 和列 k 包含数字 k」。这样，我们就可以在命题逻辑中快速写出数独的约束条件。例如，下图中的句子说明数字 5 应该出现在第一行中。

同样，我们也可以写下其他数字的其他约束条件。在我们的约束条件下，总共有 9^3=729 个原子。每一个原子可以是真或假，即表征总共 2 种可能的状态（远大于宇宙中物理原子的数量）。

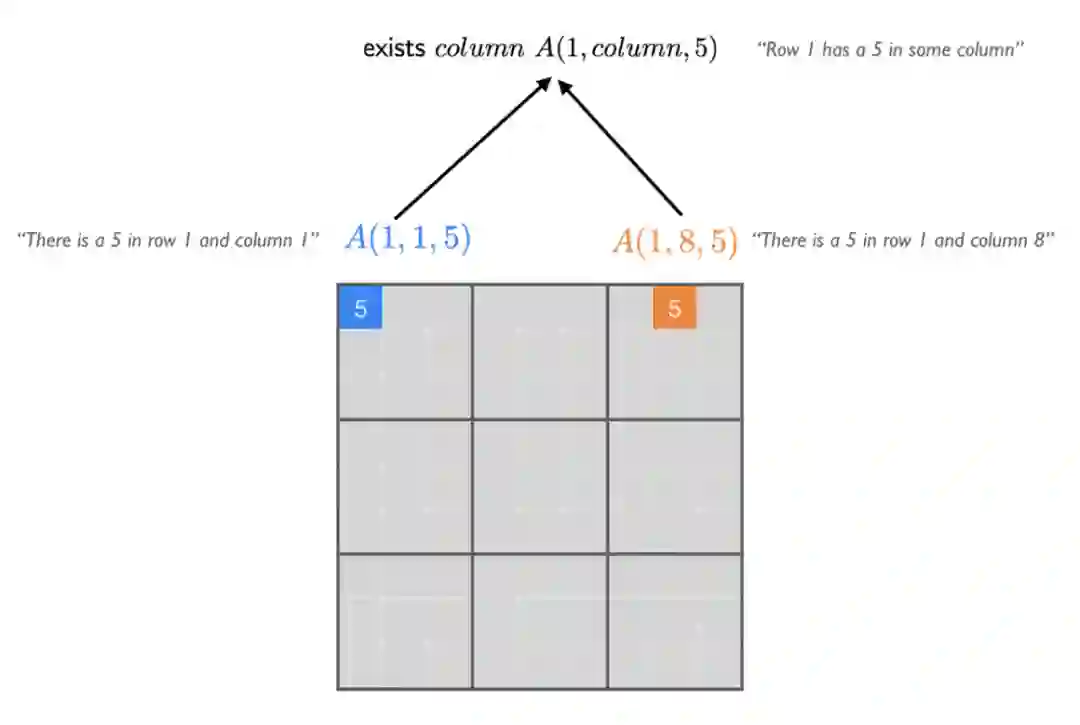
一阶逻辑通过引入原子来改进命题逻辑，这些原子可以接受域中对象的参数。在一阶逻辑中将有一个原子来接受这些变量作为参数，而不是用一个原子 A_ijk 来表示 i、j 和 k 的每个组合。例如，A(1,3,5)表示第 1 行和第 3 列中有一个 5。下图表示第 1 行中有一列的数字是 5。

一阶逻辑是许多现代逻辑系统在研究和工业中应用的基础。许多其他逻辑系统建立并扩展了一阶逻辑（例如，二阶逻辑、三阶逻辑、高阶逻辑和模态逻辑）。每一种逻辑都增加了一个新的维度或特性，以便更容易对世界的某些方面进行建模。例如，被称为时态逻辑的逻辑被用来对时间和变化进行建模。

1.2 AI/ML 中的逻辑

1.2.1 科学中的自动发现

逻辑学最成功的应用之一是在科学领域中表示结构化的科学知识。2007 年，威尔士和英格兰的一个小组创建了一个名为 Adam（自动发现和分析机器）的系统 [1]。Adam 可以自动形成科学假设，进行实验来检验假设并记录实验结果。这是第一个自动系统，用来发现各类的科学信息。Adam 成功地应用于确定酵母中的一些基因。在这个系统中，假设、实验结果和结论都以逻辑的形式表达出来。

1.2.2 归纳程序设计

归纳程序设计的目标是学习给定一组输入和输出示例的计算机程序。归纳程序设计处理的是可以从这些例子中学习的生成系统。这种系统通常是用逻辑来表述的。最先进的归纳程序设计系统可以从几个例子中学习复杂的递归程序。目前，归纳程序设计方法已经被用来学习数据清理和转换程序任务[2]。

1.2.3 数学推理自动化

上面的数独例子说明了一阶逻辑比命题逻辑更具表现力。不过，我们能用它来模拟的东西有限制吗？实际上，单是一阶逻辑就相当强大，它强大到可以模拟几乎所有的古典数学。在标准数学的概念下工作，使用一阶逻辑可以陈述你想要证明的任何目标（一个猜想），并能让机器自动检查你的工作（数学证明）。这种方法就是直接使用数学的推理自动化。

1.2.4 计算机系统（包括机器学习系统）的验证

在数学之外，以一阶逻辑和类似系统为基础的逻辑被用于验证计算机系统。这种选择被称为正式验证（Formal Verification）。在正式的验证中，有一个计算机系统 S 和一个属性 P，用户必须用一种相对严格的方式来验证这个属性是有效的。例如，用于验证硬件和软件系统的工业强度系统 ACL2 (http://www.cs.utexas.edu/users/moore/acl2/)。

1.2.5 类似逻辑系统与机器学习模型

随着越来越多的应用程序和领域使用机器学习模型，仍有一些场景需要使用类似逻辑系统和机器学习模型。例如，许多欺诈检测系统使用一个或多个机器学习模型以及大量手工编制的规则，而这些规则是非常必要的。在欺诈检测领域，这些规则可能会捕获新的和不断发展的欺诈模式，而针对这些模式可能并没有足够的数据来训练得到新的模型[3]。

最近的一些研究着眼于将逻辑与深度学习系统进行结合，这也正是我们这篇文章所考虑的问题。我们将在下面的内容中选择三篇关注于逻辑推理与深度神经网络相结合的文章进行深入分析[5][6][7]。

2. 逻辑推理与深度学习（Logic Reasoning & DL）

2.1 Bridging Machine Learning and Logical Reasoning by Abductive Learning [5]

本文是南大周志华教授组发表在 NeurIPS 2019 中的一篇研究成果。感知（Perception）和推理（Reasoning）是两种具有代表性的智能能力，它们在人类解决问题的过程中是无缝集成的。然而在人工智能领域，这两种能力通常是分别通过机器学习和逻辑编程来实现的，因此，这两类技术在人工智能的历史上是分开发展的。本文提出的诱因性学习（Abductive Learning）旨在将两类人工智能方法有机地统一起来，即机器学习模型学习从数据中感知原始逻辑事实，而逻辑推理方法则是引入符号领域知识并纠正错误感知的事实，以改进机器学习模型。此外，作者提出了一种新的方法来联合优化机器学习模型和逻辑推理模型。作者证明，通过使用诱因性学习，机器可以从简单的手写方程图像中同时学习识别数字和解决未知的数学运算。此外，所学习到的模型可以推广到更长的方程组并适应不同的任务，这已经超出了现有的先进深度学习模型的能力。

2.1.1 诱因性学习

为了更自然地利用学习和推理，了解感知和推理在单个系统中如何相互影响是至关重要的，本文所引入的诱因性学习则是一种有效的联合应用和分析的方法。诱因性学习是指根据背景知识有选择地推断出对观察结果作出最佳解释的特定事实和假设的过程，其中「观察」主要是感官信息，「知识」通常是象征性和结构性的。

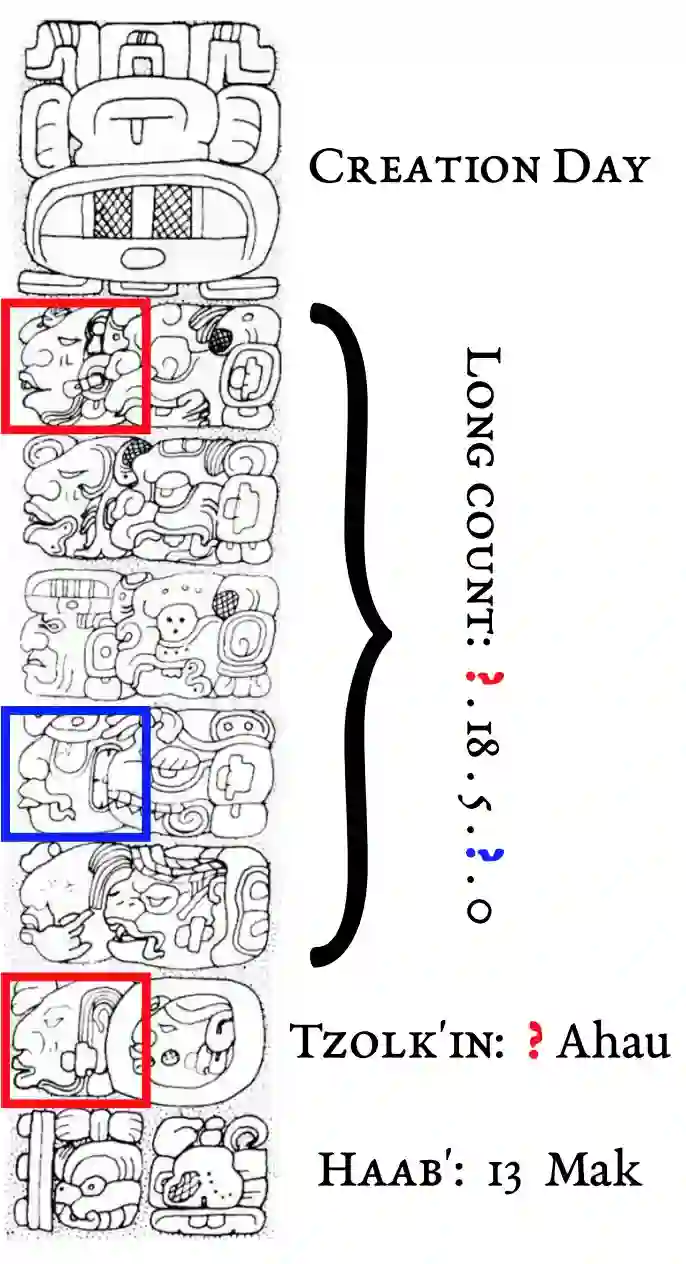
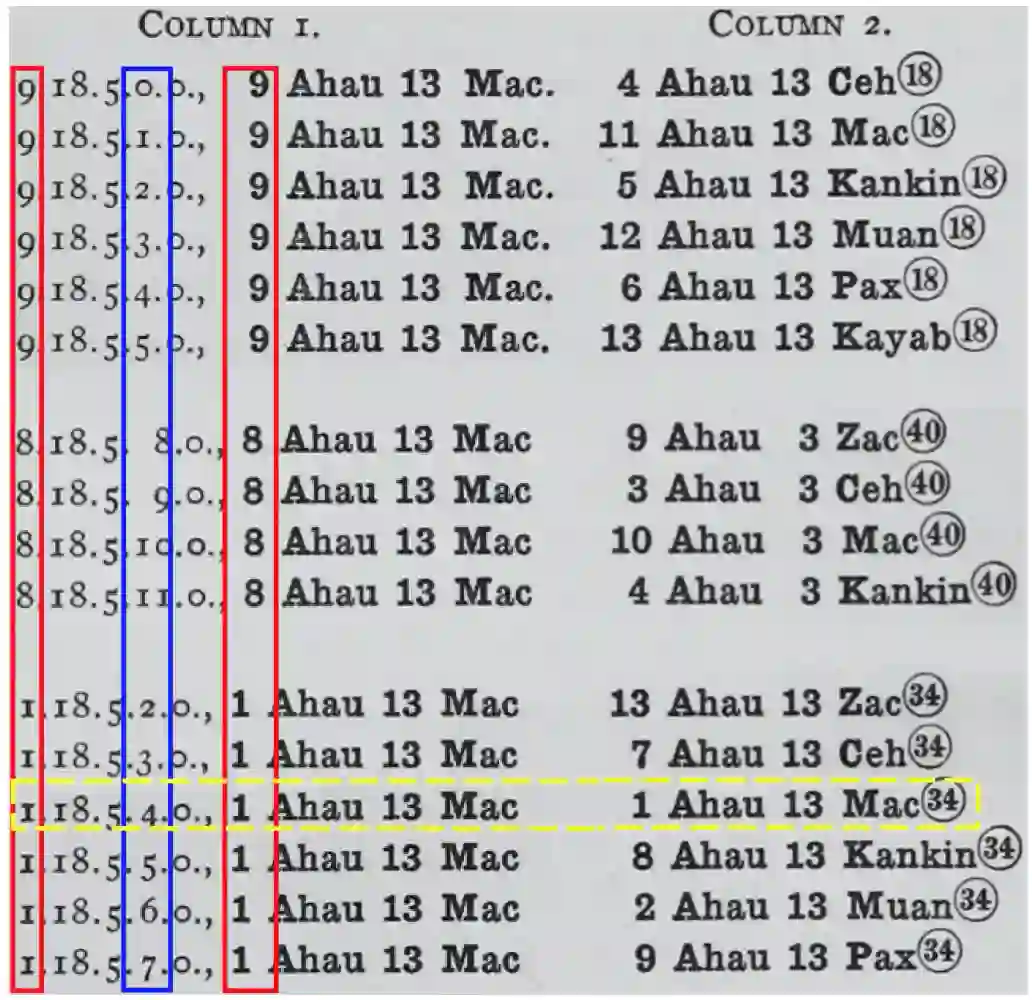
人类使用诱因问题解决方法来解决问题的一个直观例子是玛雅象形文字的破译，它反映了人类两个显著的智能能力：1）从象形文字中直观地感知单个数字；2）基于数学和日历的背景知识，象征性地进行推理。图 1 显示了从帕伦克十字庙发现的玛雅历法，它从神话中的创世日期开始，接着是以长计数书写的时间段，最后是由 Tzolk'in 和 Haab'日历编码的特定日期。

图 1. 玛雅历法，其中彩色盒子和「？」对应于未知数字

图 2 描绘了查尔斯 P. 鲍迪奇（Charles P. Bowditch）破解图 1 的记录。他首先确认了一些已知的数字，并确认第一和第六个象形文字是相同的。然后，Bowditch 尝试用视觉上相似的数字代替那些未知的象形文字，如图 2 中的「第 1 列」所示。同时，他根据自己的推测和玛雅历法中的背景知识计算出 Tzolk'in 和 Haab'的值，如图 2 的「第 2 列」所示。最后，通过观察其猜想与计算的一致性，得到了正确答案「1.18.5.4.0，1 Ahau 13 Mak」。这整个过程应用的就是诱因问题解决方法。

图 2. 鲍迪奇对图 1 的解读（他把「Mak」写为「Mac」）。垂直框中的数字是他对图 1 中未知象形文字的猜测（第 1 列）。虚线黄色框根据其计算结果（第 2 栏）标记一致结果。

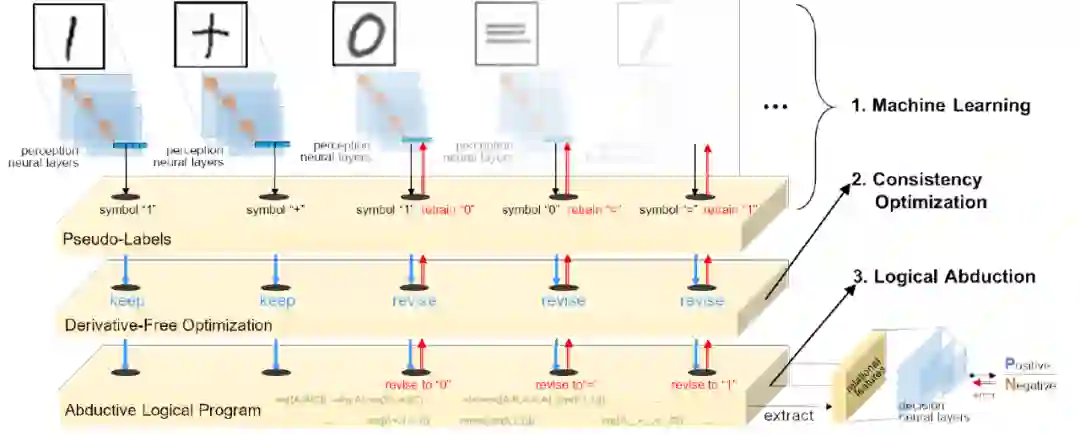
受诱因问题解决方法的启发，本文提出了诱因性学习（Abductive Learning，ABL），一种连接机器学习和逻辑推理的新方法。在 ABL 中，机器学习模型负责将子符号数据解释为原始逻辑事实，逻辑模型可以根据一些一阶逻辑背景知识对解释后的事实进行推理，以得到最终的输出。这一过程中最主要的困难在于子符号模型和符号模型很难一起训练。更具体地说：1）它不具备训练机器学习模型的原始逻辑事实（如图 1 中的正确数字）的任何基本真理；2）没有准确的原始逻辑事实，推理模型很难推断出正确的输出或学习正确的逻辑理论。

本文提出的诱因学习（ABL）试图通过逻辑诱因和一致性优化来解决这些挑战。给定一个与最终输出相关联的训练样本，逻辑推理可以对缺失的信息（例如，示例中的候选原始事实，或能够完成背景知识的逻辑子句）进行推测，以建立从样本到最终输出的一致性证明。然后，分别用导出的原始事实和逻辑子句训练机器学习模型，并将其作为符号知识存储。一致性优化被用来最大化推测与背景知识之间的一致性。为了解决这个高度复杂的问题，作者将其转换为一个任务，即搜索函数，猜测可能错误的原始事实。

由于收集玛雅象形文字数据是非常困难的，作者设计了一个类似的任务——「手写方程解谜」用于实验。该任务具体为学习图像识别（感知）和数学运算计算方程（推理）。实验结果表明，ABL 比最先进的深度学习模型具有更好的泛化能力，并且能够以一种互利的方式利用机器学习和推理。作者在一个可视化 n 皇后任务上的实验进一步证明，ABL 框架是非常灵活的，可以利用约束逻辑编程等经典符号 AI 系统来提高机器学习的性能。

2.1.2 方法简介

诱因性学习的任务可以形式化的表示如下。诱因性学习的输入由一组标记的关于目标概念 C 和领域知识库 B 的训练数据组成 D = {<x1, y1>, . . . ,<xn, yn>} 。目标概念 C 是在一组原始概念符号 P={p1，…，pr}之间的未知关系下定义的。其中每个 pk 都是 B 中定义的符号。ABL 的目标是输出一个假设模型 H=p∪∆C：

• p 是从特征空间到原始符号的映射，即它是一个传统机器学习的感知模型；

• ∆C 是一组用 B 定义目标概念 C 的一阶逻辑子句，称为知识模型。

假设模型应满足：

 (1) 

其中，符号｜= 表示逻辑暗含（logical entailment）。从公式（1）可以看出，诱因性学习的主要挑战是感知模型 p 和知识模型∆C 之间的相互依赖关系：1） 需要依赖于感知结果 p(x)来学习 ∆C，p(x)为 x 中原始概念的集合。2） 为了得到 p，需要得到用于训练的基本真值标签 p(x)，p(x)可以从 B∪∆C 和 y 的逻辑推导出来。当机器学习模型训练不足时，感知到的原始符号 p(x)极有可能不正确，因此作者将其命名为伪基元（pseudo-groundings）或伪标签（pseudo-labels）。因此，基于公式（1）的 ∆C 推理是不一致的，当知识模型∆C 不准确时，逻辑推导出的伪标签 p(x)也可能出错，从而影响了 p 的训练，而无论哪种方式都会中断学习过程。

ABL 试图通过将机器学习与诱因性逻辑推理模块相连接，并通过一致性优化将它们的内部机制融合起来，从而解决这些挑战。ABL 的完整框架见图 3。其中， 机器学习（Machine Learning）用于学习感知模型 p：给定一个输入实例 x，p 可以预测伪标签 p(x)作为 x 中可能的原始概念的真值。当伪标签包含错误时，需要重新训练感知模型，此时，所使用的标签是逻辑诱因返回的修正后的伪标签 r(x)。逻辑诱因（Logical abduction）是诱因推理的逻辑形式化表示。给定以一阶逻辑子句形式表述的观测事实和背景知识，逻辑推理将对观测事实的可能性解释扩展为基本假设。

图 3. ABL 完整框架

逻辑程序（Logic Programming）中的一个声明性框架将上述的过程形式化，称为诱因性逻辑程序（Abductive Logic Programming，ALP）[8]。形式上，诱因性逻辑程序（abductive logic program）可以定义如下：

定义 1 ：诱因性逻辑程序是一个三元组 (B,A,IC)，其中 B 是背景知识，A 是一组可扩展谓词，IC 是完整性约束。给定一些观测事实 O，程序输出为一组 A 的真值推理结果∆，如：

即，诱因性解释 ∆ 是一种假设：根据背景知识 B 和约束 IC 来解释观察 O 是如何成立的。考虑到公式（1），ABL 将关于最终概念的实例标签作为观测事实，并将假设模型 H=p∪∆C 作为推导内容。给定一个固定的∆C，ABL 可以根据 B 和 Y 推导出 p(x)；当感知模型 p 确定后，ALP 能够根据 B∪p(x)∪Y 推导出知识模型∆C。

ABL 的目标是学习与背景知识和训练实例相一致的假设。更具体地说，ABL 试图在给定背景知识 B 的情况下，最大化外推假设 H 与训练数据 D 之间的一致性：

关于 ABL 的优化过程本文不在详述，感兴趣的读者可以阅读作者原文。

2.1.3 手写方程解译任务

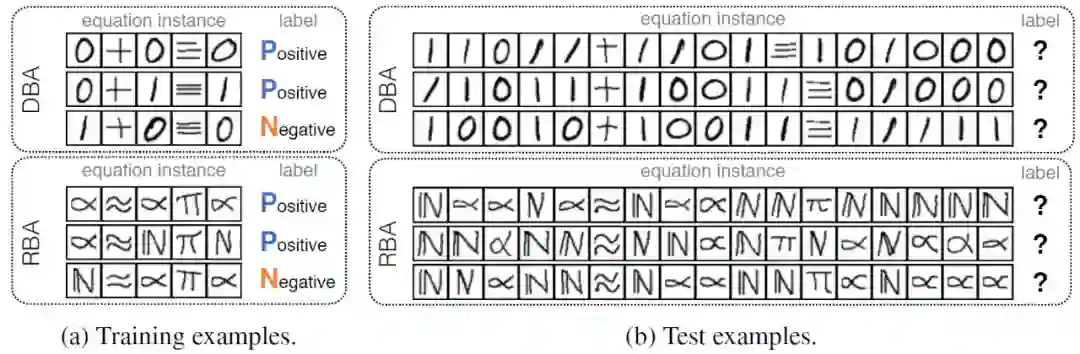
为了验证所提出方法的有效性，作者设计了一个手写方程解译任务，如图 4 所示，并应用 ABL 进行求解。解译任务的方程由连续的字符图片组成。方程由符号图像（「0」、「1」、「+」和「=」）构成并用未知的运算规则生成，每个例子都有一个表示公式是否正确的标签。机器的任务是从一组带标签的方程组中学习，并期望训练后得到的模型能够正确地预测未知的方程组。因此，这项任务需要使用图 1 中所示出的感知和推理能力来完成。

图 4. 手写方程解译难题：机器应同时学习识别符号并找出未知运算规则（本例中为「xnor」）

图 5 给出了本文中 ABL 实现的架构，它使用卷积神经网络（CNN）作为感知机器学习模型。CNN 以图像像素作为输入，期望输出为图像中的符号。符号输出构成了伪标签。逻辑推理部分是用 Prolog 语言实现的一个诱因性逻辑程序。在训练之前，将以逻辑程序形式编写的领域知识作为背景知识 B 提供给 ALP。在作者的实现中，B 只涉及方程的结构和位操作的递归定义。方程结构的背景知识是一组定句语法（Definite Clause Grammar，DCG）规则，DCG 递归地定义一个数字是「0」和「1」的序列，每个方程共享 X+Y=Z 的结构，尽管 X、Y 和 Z 的长度可能不同。位操作的知识是一种递归的逻辑程序，它反向计算 X+Y，即对 X 和 Y 从最后一位到第一位逐位运算。

图 5. ABL 结构

注：请注意，计算运算的具体规则在 B 中没有定义，即「0+0」、「0+1」和「1+1」的结果可以是「0」、「1」、「00」、「01」甚至「10」。缺失的计算规则形成知识模型 ∆C，这一部分是需要从数据中学习得到的。

训练开始后，CNN 将图像解释为伪标签「0」、「1」、「+」和「=」构造的符号方程。因为 CNN 没有经过训练，所以感知到的符号通常是错误的。在这种情况下，ALP 不能根据领域知识导出任何与训练数据一致的 ∆C。为了导出一致性的 ∆C，ABL 学习了启发式函数δ来标记可能不正确的伪标签。

当 CNN 收敛或算法满足迭代极限后，所有 < x_i , y_i > 被关系特征确定为二元特征向量。对于每个输入方程 x_i，其伪标签将由所有的关系特征来评估以产生二进制向量 u_i= [u_i1,...,u_iT]：

原始数据集 D={<x_i , y_i>}可以转换为新的数据集 D’={<u_i , y_i>}，从中可以学习一个决策模型来处理子抽样带来的噪声问题。

2.1.4 实验分析

作者构造了两个符号的图像集来建立如图 6 所示的方程。数字二进制加法（Digital Binary Additive，DBA）方程是用基准手写字符数据集中的图像创建的，而随机符号二进制加法（Random Symbol Binary Additive，RBA）方程则是从 Omniglot 数据集中随机选择字符集构建的，并与 DBA 任务中的方程具有相同结构。为了评价实验中各种对比方法的感知泛化能力，用于训练方程和测试方程的生成图像是不相交的。每一个方程都作为数字和运算符的原始图像序列输入。训练和测试数据包含长度为 5 到 26 的方程。对于每个长度，它包含 300 个随机生成的方程，总共 6600 个训练样本。

图 6. 手写方程解译任务的数据实例

本文实验中所使用的对比方法包括：

• 1）ABL，机器学习模型由两层 CNN、一个两层多层感知器（MLP）和一个 softmax 层组成，逻辑诱因将 50 个位操作的计算规则集作为关系特征，决策模型为两层 MLP。实验中尝试了两种不同的设置：使用所有训练数据的 ABL-all 和仅使用长度为 5-8 的训练方程的 ABL-short。

• 2）可微神经计算机（Differentiable Neural Computer，DNC），这是一个与记忆有关的深层神经网络。

• 3）Transformer 网络，这是一个经过关注增强的深层神经网络，已经被证实在许多自然语言处理任务中是有效的。

• 4）双向长短期记忆网络（Bidirectional Long Short-Term Memory Network，BiLSTM），这是目前应用最广泛的序列数据学习的神经网络。为了处理图像输入，BiLSTM、DNC 和 Transformer 网络也使用与 ABLs 相同结构的 CNN 作为它们的输入层。所有的神经网络都是用一个从训练数据中随机抽取的验证集来调整的。

除上述对比方法外，作者还进行了人类实验（ human ）。40 名志愿者被要求对从相同数据集中取样的方程图像进行分类。在参加测试之前，向各位志愿者提供了有关位操作的领域知识作为提示，但是具体的计算规则并不可知。作者没有使用与机器学习实验完全相同的设置，而是给了志愿者一个简化版本，其中只有 5 个正方程和 5 个负方程，长度在 5-14 之间。

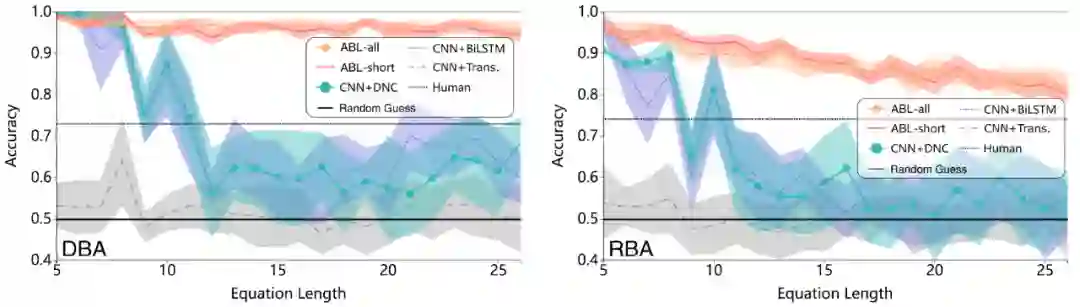
图 7. DBA（左）和 RBA（右）任务的实验结果

图 7 中的实验结果表明，在这两个任务中，基于 ABL 的方法明显优于其它进行比较的方法，并且 ABL 正确地学习了定义未知操作的符号规则。所有这些方法在 DBA 任务上的性能都比 RBA 好，这是因为 DBA 任务中的符号图像更容易区分。ABL-all 和 ABL-short 的性能没有显著差异。随着测试方程长度的增加，实验中用于比较的其它方法的性能迅速退化到随机猜测的准确度水平，而基于 ABL 的方法对未知数据的推导预测效果更好。一个有趣的结果是，人在这两个任务上的表现非常接近而且都比 ABL 差。根据志愿者的说法，他们并不需要区分不同的符号，在这种任务中人们非常容易出错，而机器在检查逻辑理论一致性方面是很擅长的。因此，应该更好的利用机器学习系统在逻辑推理方面的优势。

2.1.5 文章小结

作为心理学中一种重要的认知模型，诱因已经引起人工智能领域的关注。现有的工作大多数是在符号域中将诱因性（Abduction）与归纳（Induction）结合起来。也有一些工作使用诱因性学习改进机器学习的效果，这些方法一般需要将逻辑背景知识调整为函数约束，或者在学习和推理过程中使用特别设计的算子来支持梯度下降，从而将逻辑推理简化为不同的连续优化问题。

另一方面，ABL 利用逻辑推理和试错搜索（Trial-and-Error Search），在不使用梯度的情况下将机器学习与原始的一阶逻辑连接起来。ABL 继承了一阶逻辑推理的全部能力，例如，它有可能放弃不在背景知识中的新的一阶逻辑理论。因此，可以直接向本文介绍的 ABL 框架中引入许多现有的符号人工智能技术。

最后，ABL 框架具有通用性和灵活性。例如，感知机器学习模型可以是一个预先训练好的模型，而不必须是从头开始学习的。机器学习的任务可以是半监督的，而不必须是完全没有标签的。逻辑推理可以包括二阶逻辑子句，从而可能能够实现递归从句和谓词自动发明。作者希望其对诱因性学习的探索能够推动构建统一的学习和推理框架。

2.2 SATNet: Bridging deep learning and logical reasoning using a differentiable satisfiability solver [6]

本文是 ICML 2019 中获得最佳论文提名的一篇文章。由于上一篇文章《Bridging Machine Learning and Logical Reasoning by Abductive Learning》在 2018 年已经在 arXiv 上进行了发布，所以本文有参考引用并对比分析了与上一篇文章的不同。上一篇文章所介绍的方法是从现有的一组已知关系中创建一个模块（逻辑诱因模块），以便深层网络能够学习到这些关系的参数。因此，该方法需要植入变量之间关系的先验信息。本文所提出的方法则是端到端学习这些关系及其相关参数，即，本文引入了一个可微（平滑）最大可满足性（maximum satisfiability，MAXSAT）求解器，并将其直接集成到深度学习系统的回路中，而不是作为一个单独的分离模块所考虑。该求解器基于快速坐标下降法来解决与 MAXSAT 问题相关的半定程序（semidefinite program，SDP）。具体见第一篇文章中的「图 3. ABL 完整框架」。ABL 框架包括了两个独立的模块「Machine Learning」和「Logical Abduction」。逻辑诱因性分析是一个与机器学习 ML 完全分离的单独模块。而在这篇文章中，作者考虑，不将逻辑推理和 ML/DL 完全分离开，而是将逻辑推理作为深度学习系统完整回路中的一个部分，实现端到端的学习。

2.2.1 方法介绍

MAXSAT 问题是著名的可满足性（satisfiability，SAT）问题的优化模拟，其目标是使满足的子句数最大化。作者提出了一个可微的平滑的近似 MAXSAT 解算器，可以集成到目前的深度学习网络体系结构中。该解算器使用快速坐标下降法来求解 MAXSAT 的 SDP 松弛。考虑一个包含 n 个变量和 m 子句的 MAXSAT 实例。令 v 表示问题变量的二进制赋值，v_i 是变量 i 的真值，定义 s_i，其中 s_ij 表述子句 j 中 v_i 的符号。MAXSAT 问题定义为：

（1）

为了形成（1）的半定松弛约束，作者首先将离散变量 v_i 松弛为相关的连续变量且满足 ||v_i||=1，相对于某个「真值方向」v_T 满足 ||v_T||=1。此外，定义一个对应于 v_T 的系数 s_T。MAXSAT 的 SDP 松弛为：

  （2）

这个问题是 MIN-UNSAT 的一个低秩（但非凸）公式，它等价于 MAXSAT。可以将这个公式重写为一个 SDP，并且已经由研究人员证明给定 k>sqrt(2n)的情况下，该式可以恢复最优 SDP 解。尽管它是非凸的，可以通过坐标下降来优化地解决公式（2）。特别是，依赖于 v_i 的客观条件表示为：

其中 s_i 是 S 的第 i 列向量。根据 ||v_i||=1 的约束条件，最小化 v_i 的值以得到坐标下降更新：

这些更新可证明能够收敛到 SDP(2)（即公式（2）对应的 SDP）的全局最优不动点。

使用 MAXSAT SDP 松弛和相关的坐标下降更新，作者创建了一个用于可满足性求解的深度网络层（SATNet）。令 I 表示已知赋值的 MAXSAT 变量的指数，O≡{1,...,n}\I 对应于未知赋值的变量的指数。SATNet Layer 允许以概率或二进制的形式输入 z_l∈[0,1]，l∈I，然后输出未知变量 z_o∈[0,1]，o∈O 的赋值，这些未知变量具有类似的概率值或二进制值。令 Z_I 和 Z_O 分别表示全部的输入和输出任务。

通过 SDP(2)从输入 Z_I 生成输出 Z_O，SATNet Layer 的权重对应于 SDP 的低秩系数矩阵 S。完整的前向传递过程如图 1 所示，具体的层初始化和前向传递的步骤描述见算法 1。

图 1. MAXSAT 层的前向传递。该层将已知 MAXSAT 变量的离散或概率赋值作为输入，通过权重 S 的 MAXSAT SDP 松弛输出对未知变量赋值的猜测。

【层初始化】

初始化 SATNet 时，用户必须指定该层可以表示的最大子句数 m。通常希望将 m 的值设置的较低，因为低秩结构可以防止出现过拟合的问题，从而提高泛化能力。考虑到这种低秩结构，用户希望通过辅助变量在一定程度上提高层的表示能力。这里的高级直觉来自于布尔满足问题的合取范式（Conjunctive Normal Form，CNF）表示。向问题中添加额外的变量可以显著减少描述该问题所需的 CNF 子句的数量。

最后，令 k=sqrt(2n)+1，n 除了辅助变量外还捕获实际问题变量的数量。这也是本文的 MAXSAT 松弛公式（2）恢复其相关 SDP 的最优解所需的最小 k 值。

【放松层输入】

首先将其输入 Z_I 松弛成连续向量用于 SDP 公式（2）。也就是说，将每一层输入 z_l，l∈I 松弛到一个相关的随机单位向量 z_l，v_l∈R^k：

   （4）

公式（4）满足：

（5）

其中，(v_l)^rand 为随机单位向量。

【通过 SDP 产生连续的输出松弛】

给定连续输入松弛 V_I，使用坐标下降更新公式（3）来计算连续输出松弛 v_o。值得注意的是，坐标下降更新只计算输出变量，也就是说，不计算其赋值作为层输入的变量。

前向传递的坐标下降算法详细说明在算法 2 中。该算法保留了计算 g_o 所需的Ω=VS^T 项，然后在每次内部迭代中通过秩 1 更新对其进行修改。因此，每次迭代的运行时间是 O(nmk)。

【生成离散或概率输出】

给定坐标下降的松弛输出 V_O，层通过阈值或随机取整将这些输出转换为离散或概率变量赋值 Z_O。随机化舍入的主要思想是，对于每一个 v_o，o∈O，可以从单位球面上取一个随机超平面 r 并赋值。

（6）

给定正确的权值，这种随机取整过程保证了某些 NP-hard 问题的最佳期望逼近比。在训练期间，没有明确地执行随机取整。相反，v_o 和 v_T 在给定 r 的同一侧的概率是：

 （7）

在测试过程中，既可以以相同的方式输出概率输出，也可以通过阈值分割或随机舍入输出离散赋值。如果使用随机化舍入，则执行多次舍入后将 z_o 设为使公式（1）中 MAXSAT 目标最大化的布尔解。

最后，作者讨论了后向传递，即，通过 SATNet layer 获得反向传播更新，使其能够集成到神经网络中。基于层输出给定网络损失 l 的梯度δl/δZ_O，根据层输入和每层权重δl/δS 计算梯度δl/δZ_I。由于显式展开前向传递计算并存储中间 Jacobians 在时间和内存方面效率低下，因此作者采用了高效的坐标下降算法推导出直接计算期望梯度的解析表达式。算法 1 总结了计算这些梯度计算的步骤。

【从概率输出到连续松弛】

给定 δl/δZ_O，可以通过概率分配机制推导出 δl/δV_O：

 （8）

【通过 SDP 的反向传播】

得到 δl/δV_O 后，通过 SDP 推导出解 δl/δS：

（9）

【从松弛结果到原始输入】

最后，使用梯度 δl/δV_I 通过输入松弛过程推导梯度 δl/δZ_x：

（12）

（13）

2.2.2 实验分析

在实验部分，作者证明了 SATNet 可以集成到深度神经网络架构中进行端到端的训练。作者选择了一个可视化数独问题进行实验：即，给定一个用 MNIST 数字构造的数独板的图像表示（而不是一个热编码或其他逻辑表示），深度神经网络必须输出与之相关联的数独问题的逻辑解。

图 3 给出了一个输入示例。使用经典的深度神经网络体系架构无法解决这个问题，因为解决这个问题要求能在不将问题的逻辑结构硬编码为中间逻辑层的前提下组合多个神经网络层。本文的神经网络使用了一个连接到 SATNet layer 的卷积网络结构。具体来说，将一个用于数字分类的卷积层（使用 LeNet 架构）应用到数独输入的每个单元。然后，将该卷积层的每个单元概率输出作为逻辑输入输入到 SATNet layer。这个 SATNet layer 采用与前面描述相同的架构和训练参数。整个模型经过端到端的训练以最小化交叉熵损失，并通过 Adam 进行优化，SATNet layer 的学习率为 2x10^(−3)，卷积层的学习率为 10^(−5)。

作者将本文的方法与结合了两组卷积层的卷积神经网络进行了比较，表 1 给出了实验结果。将这些结果与 74.7% 的理论「最佳」测试精度结合起来，这解释了特定的卷积结构的数独数字分类准确率。假设板子上 81 个填充单元中平均有 36.2 个单元（如测试集中）和一个 MNIST 模型，测试准确率为 99.2%，期望一个完美的数独解算器输出正确解的时间为 74.7%。（=0.99236.2）。在 100 个周期中，本文模型在测试时能够正确求解出 63.2% 的棋盘，达到理论「最佳」的 85%。本文方法在端到端求解可视化数独板方面表现出很强的性能。另一方面，基线卷积网络在 100 个周期的过程中对训练损失的改善微乎其微。因此，本文的 SATNet 架构能够直接从图形输入中进行端到端的「游戏规则」学习，这种学习方式在以前的架构中是不可能的。

表 1. 9x 9 个数独实验的结果，将 SATNet 模型与一个普通的卷积神经网络（ConvNet）以及一个接收二进制掩码指示需要学习哪些位的网络（ConvNetMask）进行比较。

2.2.3 文章小结

本文提出了一个低阶可微 MAXSAT 层，它可以集成到神经网络结构中。该层采用块坐标下降法有效地计算了前向和后向传递。SATNet 结构可以成功地用于学习逻辑结构，即奇偶函数和 9x9 数独规则。本文还给出了一个可视化的数独任务，该任务的实验结果显示本文提出的 SATNet 层可以集成到更大的深度神经网络架构中，用于端到端的训练。

这项工作涵盖了深度学习和逻辑推理的知识。目前，一些研究人员已经提出了许多「可微逻辑推理」系统，但大多数系统仍然需要预先手工参与确定的逻辑规则和真值基础，因此这些方法在某种程度上限制了它们以真正的端到端方式进行处理的能力。本文将强大而通用的逻辑处理器（如 MAXSAT 解算器）封装在一个可微框架内，该解算器可以应用在更大的深度学习框架内进行「隐式」逻辑推理。作者认为，SATNet 为整合符号推理和深度学习（人工智能的长期目标）迈出了一步。

3. 应用数据库介绍

3.1 LogiQA: A Challenge Dataset for Machine Reading Comprehension with Logical Reasoning [7]

本文是 IJCAI 2020 中的一篇录用文章，是由来自复旦大学和西湖大学的研究人员共同完成的，主要研究目的是构建一个用于测试逻辑推理能力的阅读理解数据库 LogiQA。与上一节介绍的模型方法不同，本文主要介绍的是应用于逻辑推理和机器学习任务的数据库的构建，以及结合具体的 NLP 任务介绍将逻辑推理和机器学习方法相结合的作用和意义。

机器阅读是测试自然语言理解能力的一项基本任务，它与人类认知有着密切的关系。机器阅读可以广泛应用于开放领域问答与信息检索等后续任务中。随着 NLP 深度学习的最新进展，阅读理解研究也有了长足的发展，从能够用简单事实来回答的问题发展到需要通过多跳推理来整合不同证据的问题，以及对于人类阅读理解都非常有难度的需要利用给定段落之外所涉及的常识来回答的问题。

逻辑推理是人类阅读理解和问答的一个重要方面，也是早期人工智能的主要研究课题之一，然而目前涉及逻辑推理的 NLP 数据库非常有限。图 1 给出了一个需要通过逻辑推理才能完成的阅读理解问题。P1 由一段事实和一个问题组成，这个问题要求被测者以事实为前提选择一个有效的结论。为了选出正确的候选者，机器需要理解前提和候选者的答案。正确的答案可以通过绝对推理找到。

图 1. LogiQA 示例，红色对勾表示正确答案。

随着深度学习技术的兴起，在简单的问答 QA（Question-Answer）任务中，算法模型展现出了良好的性能，此外，也提出了大量应用于机器阅读的数据库。在一个典型的 QA 任务设置中，将一篇文章和一个问题输入系统，任务要求是从候选答案列表中选择一个最合适的答案。P2 是一个更具挑战性的问题，段落中只提供了一个前提和结论，需要在缺少一个前提的情况下选择答案。问题涉及三类工人，包括 A 宿舍区工人、B 车间工人和纺织工人。被测试者可以通过绘制三组工人之间的逻辑关联来找到答案。

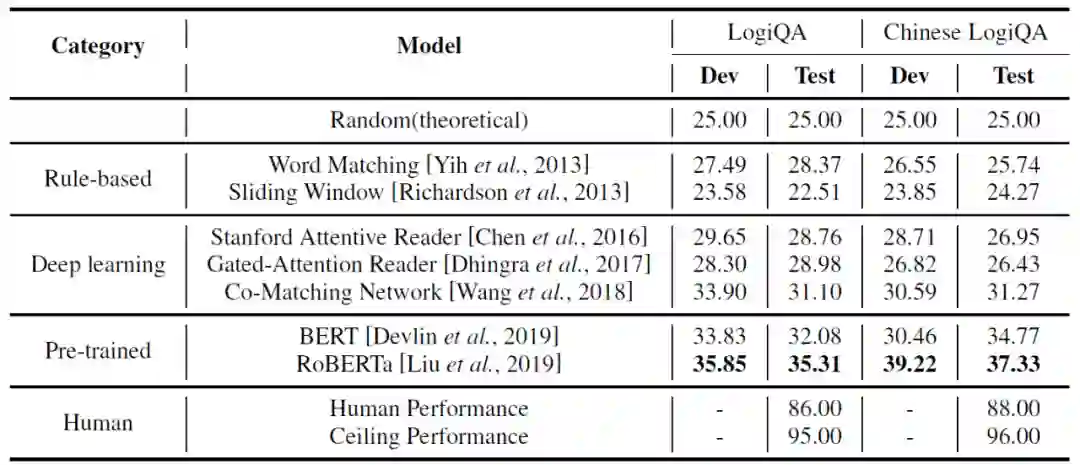
回答本文所构建的 LogiQA 所涉及的阅读理解问题需要同时具有自然语言理解（NLU）和逻辑推理能力。与简单事实的问答相比，LogiQA 中段落和候选答案之间的词汇重叠所起的作用相对较小。与常识性阅读理解相比，LogiQA 的问题不太依赖外部知识，而是需要逻辑推理来解答。LogiQA 包含 8678 个段落问题对，每个问题有四个候选答案。相关数据来源于公开提供的阅读理解逻辑试卷，这些试卷由领域专家设计，用于评估逻辑推理能力和测试参与者。问题的质量和主题覆盖是可靠的。作者从原始数据集中手动选择问题，过滤掉了涉及数字、图表或数学计算量较大的问题，并确保逻辑推理类型的广泛覆盖，包括范畴推理、条件推理、析取推理和连词推理等。

3.1.1 数据库介绍

本文作者通过收集中国国家公务员考试公开试题中的逻辑理解题来构建 LogiQA，这个考试的目的是测试公务员的批判性思维和问题解决能力。作者收集了官方网站上发布的原始数据，得到了 13918 个段落问题选择题。执行以下步骤来清理原始数据。首先，删除所有不符合问题设置格式的实例，即如果候选选项的数量不是 4，则删除该问题。其次，根据文本信息过滤掉所有包含图像或表格的段落和问题。还删除了所有包含关键字 「下划线」和「排序句子」的问题，因为对于典型的机器阅读器来说，很难重现下划线和句子编号顺序的场景。最后，作者删除了所有重复的段落问题对。最终的结果数据集包含 8678 个段落问题对。由于原始数据集是用中文编写的，因此作者还聘请了五名专业英语人士手动翻译数据集。为了保证翻译质量，又专门聘请了三名校对员。如果校对者认为翻译存在问题，则将翻译后的实例再次发送回翻译人员进行修订。作者同时发布了中文版的 LogiQA（中文 LogiQA），用于基于汉语推理的阅读理解研究。

• 范畴推理（Categorical reasoning）：目的是推理一个特定的概念是否属于一个特定的范畴。这种推理通常与量词相关，如「all/everyone/any」、「no」和「some」等。

• 充分条件推理（Sufficient conditional reasoning）：假设推理的类型是基于 「如果 P，那么 Q」形式的条件陈述，其中 P 是前因，Q 是后因。

• 析取推理（Disjunctive reasoning）：在这种推理中，前提是析取的，形式是「要么。或者。」，只要一个前提成立，结论就成立。

• 合取推理（Conjunctive reasoning）：在这类推理中，前提是连词，形式是「两个。还有。」，只有当所有前提成立时，结论才成立。

如下，表 1 总结了 LogiQA 的详细统计数据。

表 1. LogiQA 的统计数据

LogiQA 基准测试集由 867 个段落问题对组成。作者根据 Hurley 定义的逻辑推理的五种类型对实例进行人工分类[9]，包括范畴推理、充分条件推理、必要条件推理、析取推理和合取推理。这些推理属于演绎推理，即给定一套前提条件，能够得出明确的结论。因此，这种推理方法最适合于定量评价性能。图 2 给出了 LogiQA 中推理类型的统计信息和代表性示例。

图 2. LogiQA 中每种逻辑推理的例子（红色对勾表示正确答案）

3.1.2 验证的深度学习方法介绍

作者评估了典型的应用于阅读理解任务的各类模型的性能，包括基于规则的方法、深度学习方法以及基于预先训练的上下文嵌入的方法。此外，还对人类直接进行阅读理解的完成情况进行了评估，并报告了最佳性能。

【基于规则的方法】

作者采用了两种基于规则的方法，通过简单的词汇匹配给出答案。单词匹配 [10] 是基于规则的基线方法，它选择与给定段落问题对的单字格重叠程度最高的候选答案。滑动窗口 [11] 通过从给定段落问题对中的 n 个单词中提取 TF-IDF 类型特征来计算每个候选答案的匹配分数。

【深度学习方法】

深度学习方法通过文本匹配技术计算给定段落、问题和每个候选答案之间的相似度，从而找到阅读理解的答案。例如，可以使用 LSTM 编码和双线性注意力函数计算段落问题对和候选答案之间的相似性。门控注意力阅读器采用多跳结构，具有更细粒度的机制来匹配候选答案与段落问题对。协同匹配网络通过对每段文本进行编码并计算每对文本之间的匹配分数，进一步提升段落 - 问题对和段落 - 候选答案对的匹配效果。

【预训练方法】

与深度学习方法不同，预训练方法将段落、问题和每个候选答案视为一个连接句子，使用预先训练的上下文嵌入模型对句子进行编码以计算其得分。给出四个候选答案，将每个候选答案与段落和问题配对，然后构造四个连接句子，并选择模型得分最高的一个作为答案。这一类方法包括 BERT、RoBERTa 等。

【人工方法】

本文研究团队雇佣了三名研究生进行人工方法的评估，并给出了从测试集中随机选取的 500 个样本的平均分数。在计算最优性能时，如果其中一个学生给出了正确的答案，就认为人工方法针对这个问题能够给出正确答案。

3.1.3 实验分析

随机分割数据集，将其中的 80% 用于训练，10% 用于开发，其余 10% 用于测试。表 2 给出了节 3.1.2 中所讨论的模型的结果。人工方法的测试结果达到了 86.00%，最高的结果达到 95.00%，这说明对于人类测试者而言，LogiQA 的难度并不大。相比之下，其它所有算法模型的性能都比人类差得多，这表明这些方法在逻辑推理阅读理解方面相对较弱。此外，中文数据集的结果与英文数据集的结果处于同一水平。

两种基于规则的方法的准确率分别为 28.37% 和 22.51%，后者甚至低于随机猜测的基线水平。这说明单靠词汇匹配很难解决 LogiQA 中的这些问题。深度学习方法的准确率在 30% 左右，效果要优于随机猜测的方法，但远远落后于人类的表现。一个可能的原因是这些方法都是经过端到端的训练，结果发现基于注意力的文本匹配很难学习潜在的逻辑推理规则。预先训练的模型具有一定的常识性和逻辑能力，与没有上下文嵌入的方法相比，这种模型具有更好的性能。然而，RoBERTa 的最佳结果是 35.31%，仍然远远低于人类的表现。这表明预先训练的模型中的知识对于逻辑推理来说是相当薄弱的。

表 2. LogiQA 的主要结果（准确率 %）

3.1.4 文章小结

本文提出了一个大型逻辑推理阅读理解数据库 LogiQA。除了测试机器阅读的推理能力外，LogiQA 还可以作为重新审视在深度学习 NLP 时代长期追求的逻辑人工智能研究的基准水平。本文的实验结果表明，最先进的机器阅读器（各类算法、模型）仍然远远落后于人类的阅读能力。本文所提出的数据集可以作为后续测试阅读理解能力的测试基础。

4. 小结

本文在回顾什么是「逻辑」的基础上，讨论了构建有逻辑的（Logical）和可推理的（Reasoning）系统问题。其中，重点关注了两篇逻辑推理与深度神经网络相结合的文章。这两篇文章的题目很类似，所做的工作也具有一定的延续性和对比性。第一篇文章是将诱因性学习作为一个模块引入到经典的深度学习网络架构中，第二篇文章则是引入了一个可微（平滑）最大可满足性（MAXSAT）求解器，并将其直接集成到深度学习系统的回路中，而不是作为一个单独的模块所考虑。

最后一篇文章重点是结合 NLP 中的阅读理解任务构建了一个需要通过逻辑推理才能得到答案的 LogiQA 数据库。在这篇文章中作者只是使用了经典的基于规则、深度学习和预训练的方法进行实验，且效果都不好，都远低于人类直接进行阅读理解的水平，经典深度学习方法的效果甚至低于预训练的方法。但是作者并未对这种差距进行深入分析，尚无法判断是否在 NLP 这一专门领域的逻辑推理任务中预训练一定优于深度学习方法。

由我们分析的几篇文章可以看出，很显然，在强逻辑任务中机器还无法和人类相比拟。如何使深度学习 / 机器学习的方法或模型具备强大的推理能力，似乎仍然是一个悬而未决的问题。

参考文献

[1] King, R.D., Rowland, J., Oliver, S.G., Young, M., Aubrey, W., Byrne, E., Liakata, M., Markham, M., Pir, P., Soldatova, L.N. and Sparkes, A., 2009. The Automation of Science. Science, 324(5923), pp.85–89.

[2] Raza, M. and Gulwani, S., 2017, February. Automated data extraction using predictive program synthesis. In Thirty-First AAAI Conference on Artificial Intelligence.

[3] https://stripe.com/radar/guide#rules-and-manual-reviews

[4] https://medium.com/abacus-ai/an-overview-of-logic-in-ai-and-machine-learning-2f41ccb2a335

[5] Bridging Machine Learning and Logical Reasoning by Abductive Learning, 2019, NeurIPS 2019, https://papers.nips.cc/paper/8548-bridging-machine-learning-and-logical-reasoning-by-abductive-learning.pdf

[6] SATNet: Bridging deep learning and logical reasoning using a differentiable satisfiability solver, ICML 2019,   http://proceedings.mlr.press/v97/wang19e/wang19e.pdf

[7] Liu J , Cui L , Liu H , et al. LogiQA: A Challenge Dataset for Machine Reading Comprehension with Logical Reasoning[C]// Twenty-Ninth International Joint Conference on Artificial Intelligence and Seventeenth Pacific Rim International Conference on Artificial Intelligence {IJCAI-PRICAI-20. 2020.

[8] A. C. Kakas, R. A. Kowalski, and F. Toni. Abductive logic programming. Journal of Logic Computation, 2(6):719–770, 1992.

[9] Patrick J. Hurley. A concise introduction to logic. Nelson Education, 2014.

[10] Wen-tau Yih, Ming-Wei Chang, C. Meek,and A. Pastusiak. Question answering using enhanced lexical semantic models. In ACL, 2013.

[11] M. Richardson, C.J.C. Burges, and E. Renshaw. MCTest: A challenge dataset for the opendomain machine comprehension of text. In EMNLP, 2013.

分析师介绍：

本文作者为 仵冀颖，工学博士，毕业于北京交通大学，曾分别于香港中文大学和香港科技大学担任助理研究员和研究助理，现从事电子政务领域信息化新技术研究工作。主要研究方向为 模式识别 、计算机视觉，爱好科研，希望能保持学习、不断进步。

关于机器之心全球分析师网络 Synced Global Analyst Network

机器之心全球分析师网络是由机器之心发起的全球性人工智能专业知识共享网络。在过去的四年里，已有数百名来自全球各地的 AI 领域专业学生学者、工程专家、业务专家，利用自己的学业工作之余的闲暇时间，通过线上分享、专栏解读、知识库构建、报告发布、评测及项目咨询等形式与全球 AI 社区共享自己的研究思路、工程经验及行业洞察等专业知识，并从中获得了自身的能力成长、经验积累及职业发展。

感兴趣加入机器之心全球分析师网络？点击阅读原文，提交申请。