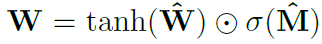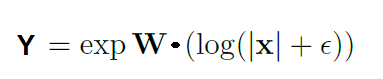针对神经算数逻辑单元（NALU）的简单指南：解释，出发点和代码

本文为 AI 研习社编译的技术博客，原标题 ：

Simple guide to Neural Arithmetic Logic Units (NALU): 

Explanation, Intuition and Code

翻译 | 老赵    校对 | 凡江    整理 | 志豪

原文链接：

https://medium.com/@faizanmukardam/simple-guide-to-neural-arithmetic-logic-units-nalu-explanation-intuition-and-code-64bc22605712

DeepMind的研究工程师，包括着名的人工智能研究员和 Grokking Deep Learning 一书的作者，Andrew Trask发表了一篇关于神经网络模型的令人印象深刻的论文，该模型可以学习简单到复杂的数值函数，具有很好的外推（泛化）能力。

在这篇文章中，我将解释NALU，它的架构，它的组件和传统神经网络的意义。 这篇文章的主要目的是提供简单直观的NALU解释（包括概念和代码），这些解释可以让对神经网络和深度学习知识有限的研究人员，工程师和学生理解。

注意：我强烈建议读者阅读原始论文，以便更详细地了解该主题。 该论文可以从这里下载。

  神经网络在哪里失败？

此图像取自此媒体帖子

理论上，神经网络是非常好的函数逼近器。 它们几乎总能学习输入（数据或特征）和输出（标签或目标）之间的任何有意义的关系。 因此，它们被用于各种各样的应用，从物体检测和分类到语音到文本转换，再到可以击败人类世界冠军球员的智能游戏代理。 有许多有效的神经网络模型诸如卷积神经网络（CNN），递归神经网络（RNN），自动编码器等满足了应用的各种需求。深度学习和神经网络模型的进步本身就是另一个主题。

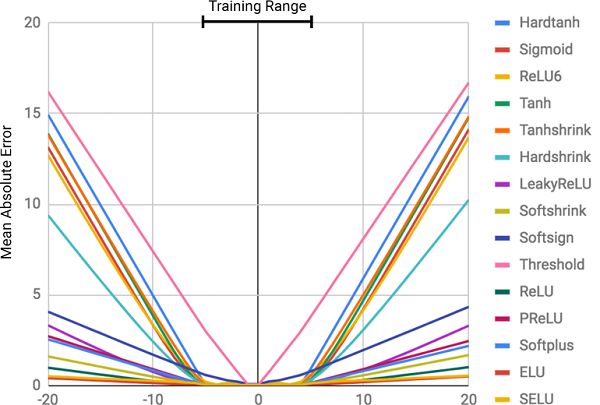
然而，根据该论文的作者，他们缺乏非常基本的能力，这似乎对人类或甚至蜜蜂都是微不足道的！ 这是计算/操纵数字的能力，也是从可观察的数字模式推断数值关系的能力。 在论文中，证明了标准神经网络甚至还在努力学习一个恒等函数（一个输入和输出相同的函数; f（x）= x），这是最直接的数字关系。 下图显示了训练用于学习这种恒等函数的各种 NN 的均方误差（MSE）。

图像显示了标准神经网络的MSE，其具有在隐藏层中使用不同激活函数（非线性）训练的完全相同的体系结构

  为什么它们失败?

NNs 未能学习这种数字表示的主要原因是在网络的隐藏层中使用非线性激活函数。 这种激活函数对于学习输入和标签之间的抽象非线性关系是至关重要的，但是当涉及将数值表示倾斜到训练数据中看到的数字范围之外时，它们会失败。 因此，这样的网络非常好地记住在训练集中看到的数字模式，但是不能很好地推断这种表示。

这就像记住答案或主题而不理解考试的基本概念。 这样做，如果在考试中提出类似的问题，则可以很好地操作，但是，如果要求扭曲的问题被设计为测试知识而不是候选人的记忆能力，则会失败。

该失败的严重程度直接对应于所选激活函数内的非线性程度。 从上面的图像可以清楚地看出，诸如 Tanh 和 Sigmoid 之类的硬约束非线性函数比诸如PReLU和ELU的软约束非线性函数具有非常小的推广能力。

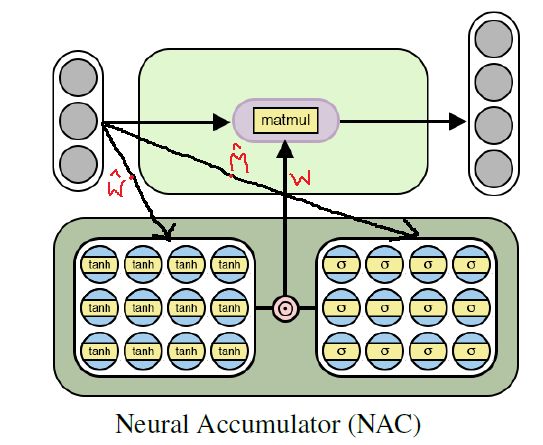
  解决方案：神经累加器（NAC）

神经累加器（NAC）构成 NALU 模型的基础。 NAC是一个简单但有效的神经网络模型（单元），它支持学习加法和减法的能力 — 这是有效学习线性函数的理想属性。

NAC是一个特殊的线性层，其权重参数具有1,0或-1的限制。 通过以这种方式约束权重值可以防止层改变输入数据的比例，并且无论多少层堆叠在一起，它们在整个网络中保持一致。 因此，输出将是输入矢量的线性组合，其可以容易地表示加法和减法操作。
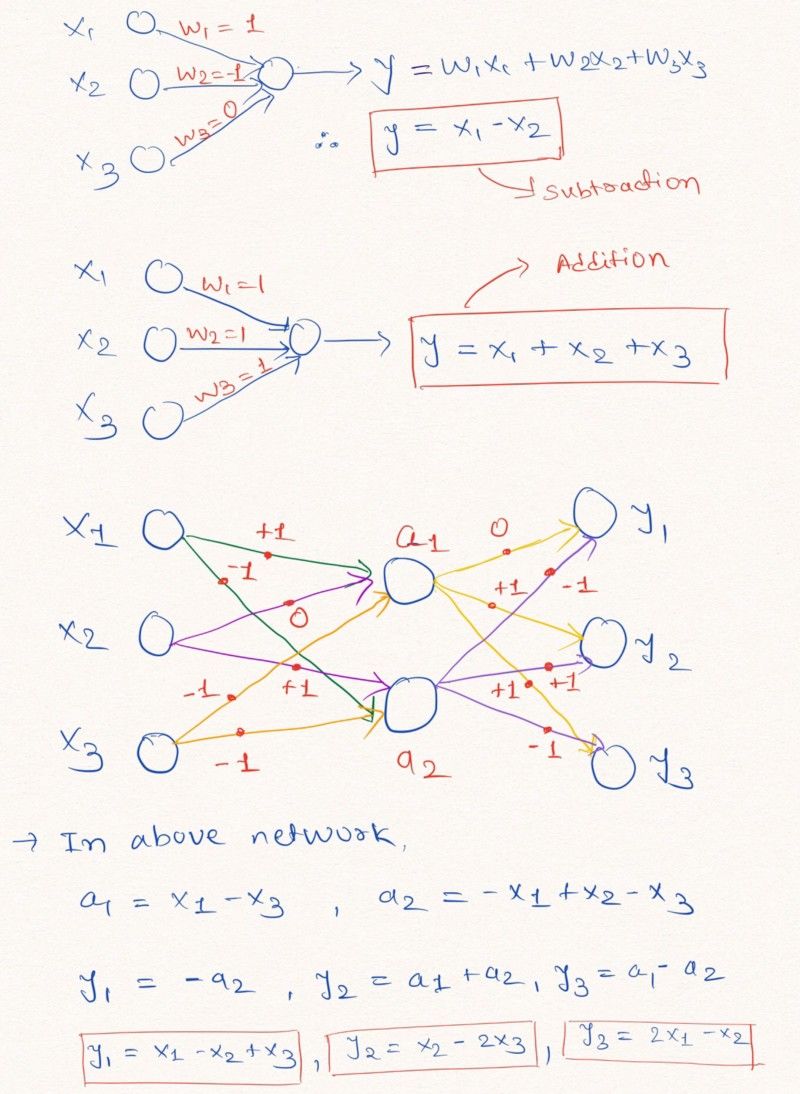
直观：为了理解这一事实，让我们考虑以下 NN 层的例子，它们对输入执行线性算术运算。

图解说明没有偏差且权重值为-1,0或1的神经网络层可以学习线性外推。

如上面的NN层所示，网络可以通过将权重参数限制为-1,0和1来学习外推简单的算术函数，如加法和减法（y = x1 + x2和y = x1 - x2）。
注意：如上面的网络图所示，NAC不包含偏差参数（b），并且没有应用于隐藏层单元输出的非线性。

由于标准神经网络很难学习NAC中权重参数的约束，因此作者描述了使用标准（无约束）参数W_hat和M_hat来学习这种受限参数值的非常有用的公式。 这些参数类似于任何标准NN权重参数，可以随机初始化并且可以在训练过程中学习。 根据W_hat和M_hat获得W的公式如下：

公式表示两个矩阵之间的元素乘积
使用上面的方程来计算网络中的权重参数，保证这些参数的值将在[-1,1]的范围内，更倾向于-1,0和1.此外，该等式是可微分方程 （其导数可以根据权重参数计算）。 因此，NAC将更容易使用梯度下降和反向传播来学习W. 下面是NAC单元的架构图。

NAC架构学习简单（线性）数字函数

  使用Tensorflow在python中实现NAC

可以想象，NAC是一个简单的NN模型，几乎没有什么调整。 下面我展示了使用Tensorflow和Numpy库在python中简单实现单个NAC层。

import numpy as np
import tensorflow as tf
nac_simple_single_layer(x_in, out_units):
    '''    Attributes:        x_in -> Input tensor        out_units -> number of output units    Return:       y_out -> Output tensor of mentioned shape       W -> Weight matrix of the layer
    '''
in_features = x_in.shape[1]

    W_hat = tf.get_variable(shape=[in_shape, out_units],
    initializer= tf.initializers.random_uniform(minval=-2,maxval=2),
    trainable=, name=)

    M_hat = tf.get_variable(shape=[in_shape, out_units],
    initializer= tf.initializers.random_uniform(minval=-2,maxval=2),
    trainable=, name=)

    W = tf.nn.tanh(W_hat) * tf.nn.sigmoid(M_hat) y_out = tf.matmul(x_in, W)

    y_out,W

在上面的代码中，我使用了可训练参数W_hat和M_hat的随机统一初始化，但是可以对这些参数使用任何推荐的权重初始化技术。 对于完整的工作代码，请查看我在本文末尾提到的 GitHub仓库。

  超越加法和减法：NAC用于复杂的数字函数

尽管上述简单神经网络模型能够学习诸如加法和减法之类的基本算术函数，但是希望能够学习更复杂的算术运算，例如乘法，除法和幂函数。

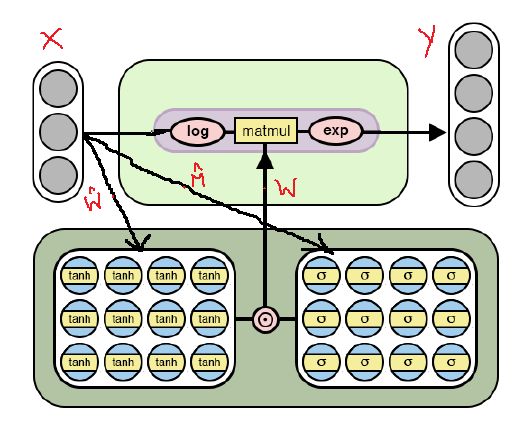
下面是NAC的修改结构，它能够使用日志空间（对数值和指数）为其权重参数学习更复杂的数字函数。 观察这个NAC与帖子中首先提到的NAC有何不同。

NAC结构学习更复杂的数字函数

如上图所示，该单元格在与权重矩阵W进行矩阵乘法之前将对输入数据进行对数函数，然后在结果矩阵上应用指数函数。 获得输出的公式在下面的等式中给出。

上面显示的复数NAC的输出方程。 这里的Epsilon是一个非常小的值，可以避免训练期间的log（0）情况。
因此，就简单NAC和复杂NAC的基本机制而言，一切都是相同的，包括W_hat和M_hat的受限权重W的公式。 唯一的区别是复杂的NAC在层的输入和输出上应用对数空间。

  复杂 NAC 的 Python 实现

与两个 NAC 的体系结构一样，复杂 NAC 的 python 实现几乎相同，只是输出张量公式中提到的变化。 以下是此类 NAC 的代码。

nac_complex_single_layer(x_in, out_units, epsilon = 0.000001):

    mWin_features = x_in.shape[1]

    W_hat = tf.get_variable(shape=[in_shape, out_units],
    initializer= tf.initializers.random_uniform(minval=-2,maxval=2),
    trainable=, name=)

    M_hat = tf.get_variable(shape=[in_shape, out_units],
    initializer= tf.initializers.random_uniform(minval=-2,maxval=2),
    trainable=, name=)

#Get Unrestricted parameter matrix W
    W = tf.nn.tanh(W_hat) * tf.nn.sigmoid(M_hat)

    x_modified = tf.log(tf.abs(x_in) + epsilon)

    m = tf.exp( tf.matmul(x_modified, W) )

    m, W

再次，对于完整的工作代码，请查看我在本文末尾提到的GitHub仓库。

  总结：神经算术逻辑单元（NALU）

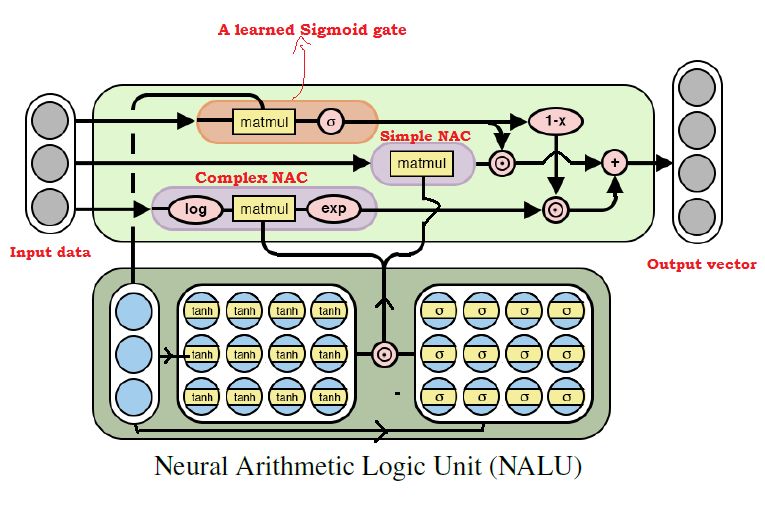
到目前为止可以想象，将两个NAC模型组合在一起可以学习几乎所有的算术运算。 这是NALU背后的关键思想，它包括由学习的门信号控制的上述简单NAC和复杂NAC的加权组合。 因此，NAC构成了NALU的基本构建块。 所以，如果你已经正确理解了NAC，NALU很容易掌握。 如果还没有，请花点时间再次阅读NAC的两个解释。 下图描述了NALU的结构。

NALU的注释图

如上图所示，在NALU中，两个NAC（紫色单元）由学习的S形门控（橙色单元）内插（组合），使得NAC的输出可以基于数值函数由门激活或去激活。 正在努力训练网络。
如上所述，简单的NAC计算累加函数，因此它负责存储NALU的线性（加法和减法）运算。 虽然复杂的NAC负责执行更复杂的数字函数，例如乘法，除法和幂函数。 NALU中底层单元的输出可以用数学表示如下：

Simple NAC : a = W X
Complex NAC: m = exp ( W log (|X| + e) )
Where, W = tanh(W_hat) * sigmoid(M_hat)
Gate cell: g = sigmoid(GX) # Where G is standard trainable parameter matrix
# And finally the output of the NALU
 = g * a + (1-g) * m   # Where is the element wise product

在NALU的上述公式中，我们可以说如果门输出g = 0，那么网络将只学习复杂的功能而不是简单的功能。 相反，如果g = 1，那么网络将只学习加法函数而不是复杂函数。 因此，总的来说，NALU可以学习任何由乘法，加法，减法，除法和幂函数组成的数字函数，这样可以很好地推断出训练期间看到的数字范围之外的数字。

  NALU 的Python实现

在NALU 的实现中，我们将使用前面代码片段中定义的简单和复杂NAC。

nalu(x_in, out_units, epsilon=0.000001, get_weights=):
    in_features = x_in.shape[1]

    a, W_simple = (x_in, out_units)

    m, W_complex = (x_in, out_units,     epsilon= epsilon)

    G = tf.get_variable(shape=[in_shape, out_units],
    initializer= tf.random_normal_initializer(stddev=1.0),
    trainable=, name=)

    g = tf.nn.sigmoid( tf.matmul(x_in, G) )

    y_out = g * a + (1 - g) * m

    (get_weights):
        y_out, G, W_simple, W_complex
    :
        y_out

同样，在上面的代码中，我对门参数G使用了随机正常初始化，但是可以使用任何推荐的权重初始化技术。

我相信 NALU 是人工智能的一个现代突破，特别是神经网络，似乎非常有前景。它们可以为许多应用打开大门，这些应用对于标准NNs来说似乎很难处理。
作者已经展示了在神经网络应用的不同领域实施 NALU 的各种实验和结果，从简单的算术功能学习任务到计算所提供的 MNIST 图像系列中的手写数字的数量，使网络学习评估计算机程序。
结果令人惊讶，并证明NALU在几乎所有涉及数字表示的任务中都优于标准NN模型。我建议读者了解这些实验及其结果，以深入了解 NALU 如何在一些有趣的数字任务中发挥作用。
但是，NAC 或 NALU 不太可能成为完成每项任务的完美解决方案。相反，它们展示了用于创建旨在用于数值函数的目标类的模型的一般设计策略。

下面是我的GitHub仓库的链接，该存储库显示了本文中显示的代码片段的完整实现。
https://github.com/faizan2786/nalu_implementation
欢迎你尝试各种功能，使用不同的超参数来测试我的模型，以调整网络。
如果你对以下评论中的这篇文章有任何疑问或想法，请告诉我，我会尽力解决这些问题。
PS：这是我关于任何主题的第一篇博文。 因此，欢迎任何关于我的写作的技术和非技术方面的建议。

想要继续查看该篇文章更多代码、链接和参考文献？

戳链接：

http://www.gair.link/page/TextTranslation/885

AI研习社每日更新精彩内容，点击文末【阅读原文】即可观看更多精彩内容：

PyTorch 中使用深度学习（CNN和LSTM）的自动图像捕获

你想要的Python编程技巧，我都给你整理好了

针对神经算数逻辑单元（NALU）的简单指南：解释，出发点和代码

Tensorflow 与 Keras 在图像分类中的对比

等你来译：

从零开始用Python写一个聊天机器人（使用NLTK）

正则表达式教程：实例速查

如何用序列到序列模型来构建数据产品

使用 Python 完成自动特征工程——如何自动创建机器学习特征