流计算引擎数据一致性的本质

流计算的应用与实践在大数据领域越来越常见，其重要性不言而喻，常见的流计算引擎有 Google DataFlow、Apache Flink，Apache Kafka Streams，Apache Spark Streaming 等。流计算系统中的数据一致性一般是用消息处理语义来定义的，如某引擎声称可以提供「恰好一次（Exactly-once Processing Semantics）流处理语义，表示（或暗示）引擎具备保证数据一致性的能力。事实上，「恰好一次（Exactly-Once）」并不等价于流计算的输出数据就符合一致性的要求，该术语存在很多理解和使用上的误区。

本篇文章从流计算的本质出发，重点分析流计算领域中数据处理的一致性问题，同时对一致性问题进行简单的形式化定义，提供一个一窥当下流计算引擎发展脉络的视角，让大家对流计算引擎的认识更为深入，为可能的流计算技术选型提供一些参考。文章主要分为三个部分：第一部分，会介绍流计算系统和一致性难题的本质；第二部分，会介绍一致性难题的通用解法以及各种方案间的取舍；第三部分，会介绍主流的流计算引擎是如何对通用解法进行泛化以实现一致性。

一流计算中的一致性

在认识流计算系统一致性之前，我们需要精确定义流计算。流（Streaming）计算是一种在无边界数据（unbounded data）上进行低延迟计算的数据处理过程。相应的，批计算更准确的说法是有界数据（bounded data）的处理，亦即有明确边界的数据处理，流和批只是两种不同数据集的传统数据计算方法，它们并不是泾渭分明的，譬如也可以通过批量的方式（e.g. Spark Streaming 中的 micro-batch）来实现无界数据上的流处理过程。

1 一致性定义及挑战

如果我们将流计算的过程（获取输入数据、处理数据、输出计算结果）视为数据库的主从同步过程，抑或视为一种从流数据生成衍生数据集（表）的过程，则流计算中的数据一致性同关系型数据库事务 ACID 理论中的 Consistency 有异曲同工之妙，后者指的是在事务开始或结束时，数据库中的记录应该在一致状态，相应地，流计算中的一致性可以定义为：流计算系统在计算过程中，或是出现故障恢复计算后，流系统的内部状态和外部输出的数据应该处在一致的状态。譬如，当故障恢复后开始重新计算，计算的结果是否满足数据的一致性（即用户无法区分恢复前和恢复后的数据）？记录是否会重复/丢失，第三方系统对同一条计算结果的多次获取，是否会存在值上的不一致？对一致性有了清晰的认知和定义后，我们来看看为什么实现一致性这么难。

在定义一中我们可以看到，流计算输入的数据是无边界的，所以系统中会存在消息抵达流计算系统延迟、顺序错乱、数量/规模未知等不确定因素，这也是流计算系统一致性复杂性远远大于批处理系统的原因：批处理系统中的输入是确定的，计算过程中可以通过计算的原子性来保证数据的一致性（如 Spark 中的 RDD 血缘）。此外，同其他分布式应用一样，流计算系统经常也会受到各类意外因素的影响而发生故障，比如流量激增、网络抖动、云服务资源分配出现问题等，发生故障后重新执行计算，在存在不确定输入的前提下设计健壮的容错机制难度很大。

除了数据输入带来的挑战，流计算输出的数据会被实时消费，类似这样不同于批处理的应用场景，也给数据的一致性带来的诸多挑战，如出现 FO 后，是撤回之前发出的数据，还是是同下游进行协商实现一致性，都是需要考虑的。

2 一致性相关概念祛魅

正确认识流计算系统一致性的内在含义和其能力范畴，对我们构建正确且健壮的流计算任务至关重要。下面我会介绍几组概念，以便于大家更好地理解流计算系统的一致性。

恰好一次≠恰好一致

今天大多数流计算引擎用「Exactly-Once」去暗示用户：既然输入的数据不是静态集合而是会连续变化的，那对每一条消息「恰好处理」了一次，输出的数据肯定是一致的。上述逻辑的推导过程是没问题的，但并不严谨，因为 Exactly-Once 作为一个形容词，后面所连接的动词或者宾语被故意抹去了，不同的表达含义也会大相径庭。

例子1，后接不同的动（名）词：Exactly-once Delivery 和 Exactly-once Process 。前者是对消息传输层面的语义表达，和流计算的一致性关系不是很大，后者是从流计算的应用层面去描述数据处理过程。

例子2，后接不同的名词：Exactly-once State Consistency 和 Exactly-once Process Consistency。前者是 Flink 在官网中对其一致性的叙述，后者是 Kafka Streaming 的一致性保证，前者的语义约束弱于后者。Exactly-once State Consistency 只是表达了：流计算要求对状态的更新只提交一次到持久后端存储，但这里的状态一般不包括「输出到下游结果」，而仅指引擎内部的状态，譬如各个算子的状态、实时流的消费偏移等，流计算引擎内部状态变更的保证，并不能等价于从输入到输出的一致性，端到端一致性需要你自己关心。

总之，如何我们后面再看到 Exactly-once XXX，一定要警惕引擎想要透露出什么信息。

端到端的数据一致性

端到端一致性（End-To-Ene Consistency），即将数据的输出也作为流计算引擎的一致性设计的一部分，正确的结果贯穿着这整个流计算应用的始终：从输入、处理过程、输出，每一个环节都需要保证其自身的数据一致性，同时在整个流计算流程中，作为整体实现了端到端的一致性。

下面叙述中，如果不是特意说明，一致性指的是引擎自身状态的一致性，端到端一致指的是包含了输出的一致性。

二流计算系统的本质

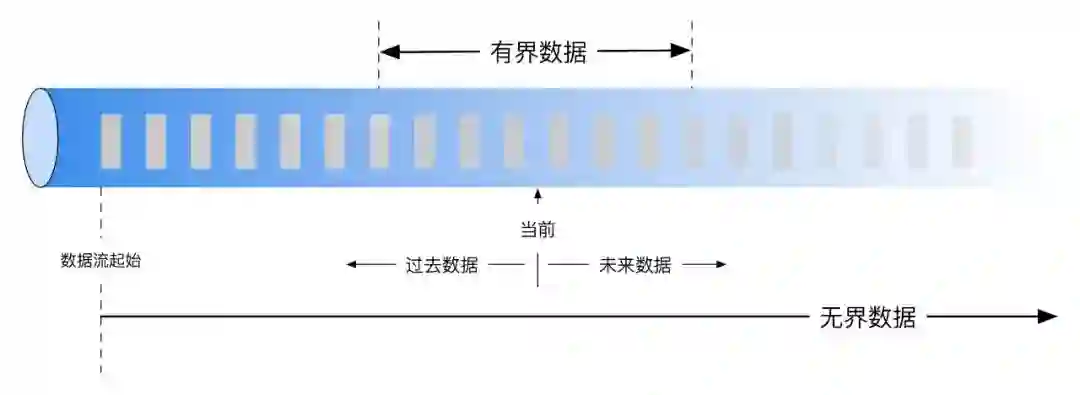
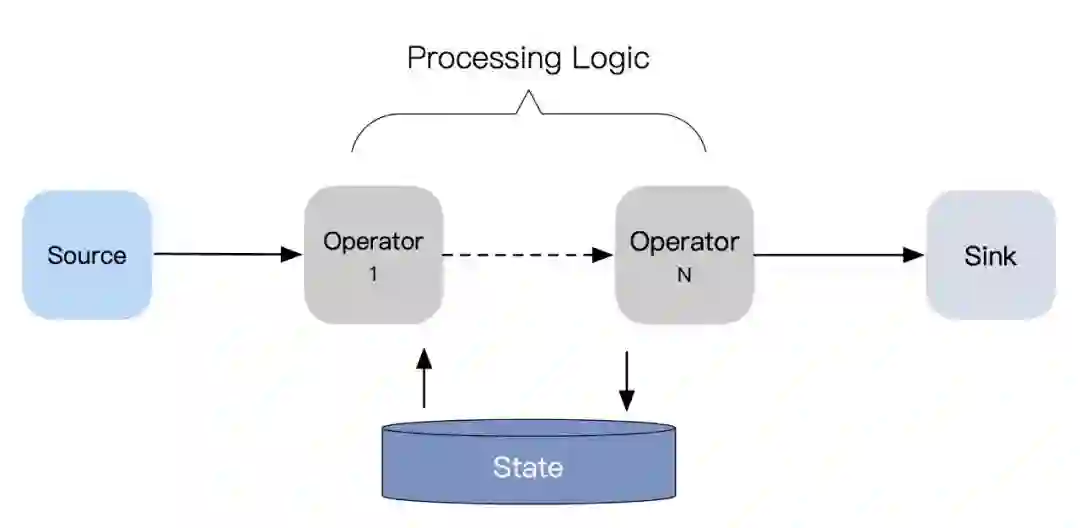
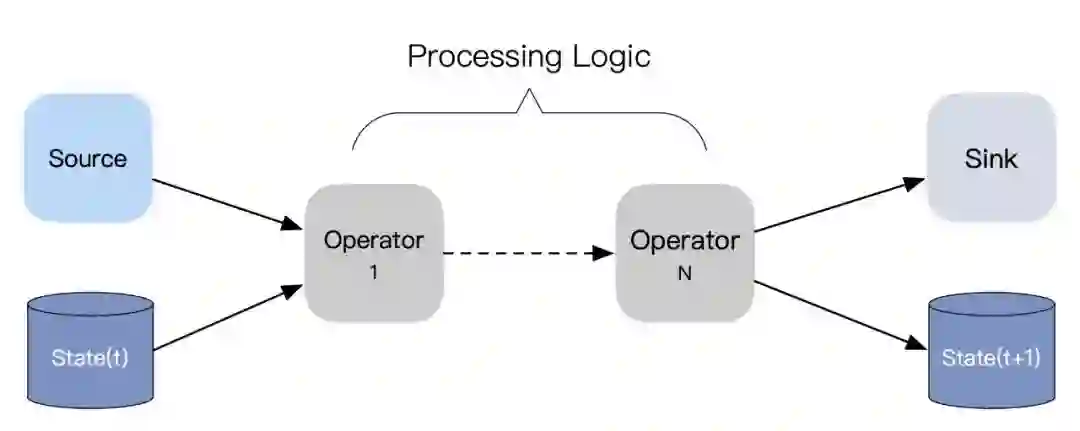
前面我们定义了流计算一致性的概念，这一部分将会从概念出发将问题进行形式化拆解，以便得到通用化的解法。

1 再次认识流计算

上面提到，流计算的输入数据是没有边界的，这符合我们传统上对流计算认知。在《System Streaming》一书中，作者提出了一个将流批统一考虑的流计算理论抽象，即，任意的数据的处理都是「流（Stream）」和「表（Table）」间的互相转换，其中流用来表征运动中的数据，表用来表征静止的数据：

流 -> 流：没有聚合操作的数据处理过程；
流 -> 表：存在聚合操作的数据处理过程；
表 -> 流：触发输出表数据变化的情况；
表 -> 表：不存在这样的数据处理逻辑。

在这个统一的理论框架下，批处理过程的一致性也可以纳入本文讨论的范畴中来。但无论是纯粹的流计算，还是上面统一的数据处理模型，我们都可以将流（批）数据处理的过程抽象为「读取数据-处理数据-输出数据」这样的三个部分，可用下面的有向无环图来表达，其中点代表数据加工逻辑，边表示数据流向，数据处理过程中的中间状态（State）一般需要做持久化存储。

2 确定性/非确定性计算

流计算中的确定性指的是，给定相同的一组数据，重复运行多次或者打乱数据进入引擎的顺序，计算完成后将会输出相同的结果，否则就是非确定性计算。常见的非确定性计算包括使用了随机数、使用系统时间、字符串拼接等。如果流计算中存在非确定性的计算，则会给端到端一致性的实现造成很多困难，部分引擎并不能很好地支持此类场景。

3 一致性问题的形式化定义

在存在不确定性计算的流计算中，不确定性计算的（中间）结果可视为流计算引擎状态的一部分。从整体上看，任何一个时间点的引擎状态等于之前所有事件计算结果（中间结果和输出结果）的累计。如果定义流计算的输入集合为：E，t 时刻以来的输入集合为 E(t)，输出集合为 Sink(t)，引擎此时状态为 State(t)，State(t) 包括各个算子的状态（包括上面提到的不确定性计算）、数据源的消费偏移量（或文件读取偏移等）等：

State(t) = OperatorState(t) + SourceState(t)

则定义流计算引擎的计算过程为，存在计算计算逻辑 F 使得：

F(E(t), Sink(t), State(t)) = Sink(t+1) + State(t+1)

令 O(t) = Sink(t) + State(t)，即将计算对引擎状态的更新视为一种特殊的输出，则流计算过程可简化为：

F(E(t), O(t)) = O(t+1)

结合流计算上面流计算一致性的定义，我们希望在引擎发生故障 FailOver 时，存在一种恢复函数 R 使得

R(E(t), O(t)) = O'(t+1)，且 O'(t+1) = O(t+1)

我们在这里将引擎状态作为一种特殊输出的考虑有两点。其一，引擎的状态一般也是输出到外部存储如 RocksDB/HDFS，这和计算下游的输出别无二致。其二，通过屏蔽引擎内部的容错机制实现，简化端到端一致性问题的抽象过程，便于更好地理解问题本身。

三一致性的通用解法

1 通用解法的推导

我们在上面定义了端到端一致性难题：R(E(t), O(t)) = O(t+1)。从输出结果的使用方（引擎内部和引擎下游数据消费方）的视角来看：对于记录 O(t+1)，当在故障发生的时间小于 t （数据没有输出）或者大于 t + 1（数据已经输出了），数据肯定是一致的。

当在 t ~ t + 1 时刻发生故障，恢复函数 R 可以屏蔽此次故障产生的副作用，让使用方认为没有故障发生，可以得到正确的 O(t+1)，显然，解决的思路是：将 E(t) 和 O(t) 作为输入，重新执行计算 F，则可以得到正确的 O(t+1)，具体地，E(t) 可以通过回拨数据偏移量得到，O(t) 需要从持久化存储中获取。O(t) 是否可以通过递归重算得到呢，即 O(t) = F(E(t-1), O(t-1)) ，答案是不可以，因为计算过程中可能存在不确定的计算逻辑，如果重算，则有一定概率 O(t) ≠ F(E(t-1), O(t-1)) 。

因此，我们得到流计算引擎要实现端到端一致性数据处理语义的充分必要条件：在流计算过程中，需要实时存储每一条中间和最终计算结果，如果考虑吞吐率不能存储每一条，则需定期以事务的方式进行批量存储。对于每一个 O(t) 存储后，恢复函数 R 的实现就简单多了：任务恢复时，将 O(t) 重新加载，使用 F 执行重算操作。

2 通用解法的工程实现

我们将端到端一致性问题的解法结合工程实践，分析一下通用解法下的若干实现场景。

在通用解法中，我们需要存储每一次计算的中间结果，这对引擎的架构设计、配套基建能力有着很高的要求，如需要高可用、高吞吐的存储后端用于状态存储。因此，我们将条件退化为可以通过事务的方式进行批量存储，这是因为事务的 ACID 特性能保证结果能以原子提交的方式作用于下游算子或者是外部的消息系统/数据库，在保证了结果（状态）一致性的前提下，能达到较高的吞吐率。

进一步分析，每一次存储或者批量事务存储 O(t) 时，引擎到底做了什么？前面我们定义了 O(t) = Sink(t) + State(t) -> O(t) = Sink(t) + OperatorState(t) + SourceState(t) ，对于引擎来说，当出现 FailOver 时，都会通过 SourceState(t) 回拨数据源偏移量进行部分重算，即消息读取语义是 At-Least-Once 的，当重复计算时，前面存储的结果（每一次计算）或者空的结果（批量事务）可以实现幂等变更的效果：如果结果已经存在了，则使用已有的结果，消除不确定性计算带来的副作用，如果之前的结果不存在，就更不会对外部系统有影响了。

如果我们的计算过程都是确定性的，那么上述的充分必要条件会有什么变化呢？在确定性计算的前提下，如果引擎输出结果的接受端是可以实现为幂等，则很多约束条件会有所简化。由于 O(t) = Sink(t) + State(t) ，引擎内部很好实现幂等状态更新，若引擎下游系统也实现了数据幂等，当在 t ~ t + n 间内出现 FailOver 时，引擎可以通过重新计算 t ~ t + n 之间的所有值，直接输出给下游使用。

因此，在仅有确定性计算的流计算系统中，实现端到端的充分必要条件可退化为：在流计算过程中，需要外部的最终结果接受端实现幂等，实时存储每一条中间和最终计算结果，如果考虑吞吐率不能存储每一条，则需定期批量存储，上述条件中去掉了对「事务」的要求的原因：如果在提交这一批数据的提交过程中又发生了异常，譬如只有部分节点的结果输出了，其他节点发生了故障结果丢失，则可以通过回到上个批次提交的状态，重算此批次数据，重算过程中，由于仅存在确定性计算，所以无论是引擎内还是引擎外，是可以通过幂等来保证数据的的一致性的。

在实际的流计算引擎实现中，对于结果内容的定义大都是一致的，主要包括输入源的消费偏移 SourceState(t)，e.g. Kafka Offset，算子状态 OperatorState(t)，e.g. Spark RDD 血缘，输出的结果 Sink(t)，e.g. Kafka 事务消息，但是在结果的存储方式上各有所不同，下面我们来看一看目前业界主流的几个流计算引擎的设计考量。

四一致性的引擎实现

目前流计算引擎的种类非常多，不是所有的引擎都可以实现端到端一致的流处理，在具备此能力的引擎中，从技术成本、引擎架构、能力范围考虑，会有不同的取舍和实现，如 Flink 中使用了轻量级的「分布式一致性快照」用于状态管理，Kafka Streams 为何没有使用呢？实现了幂等输出就一定能实现端到端一致么？本章节会一一解答上述问题。

1 Google MillWheel

Google在2013年发了一篇名为《MillWheel: Fault-Tolerant Stream Processing at. Internet Scale》的文章，论述了在 Google 内部实现低延迟数据处理的编程模型和工程实现，后面 Google 在此基础上抽象出了 DataFlow 流处理模型（具体参考论文《The Dataflow Model: A Practical Approach to Balancing Correctness, Latency, and Cost in Massive-Scale,Unbounded, Out-of-Order Data Processing》），后者对流计算流域的影响堪比20世纪初 GFS，BigTable 以及MapReduce 三篇论文对大数据的影响，后面 Google 又在 MillWheel 之上继续发展，开源了 Apache Bean 这个系统级的流批一体数据解决方案，因为 MillWheel 是更纯粹的「流计算」，所以我们重点来分析 MillWheel。

MillWheel 使用了一种名为「Strong production」的机制将每个算子的输出在发送至下游之前都进行了持久化存储，一旦发生了故障，当需要恢复时，引擎可以直接将存储后的结果发出去。回头再看端到端一致性数据处理语义的充分必要条件，显然 MillWheel 是符合「实时存储每一条中间和最终计算结果」这个条件的。对于存在不确定性计算的流计算场景，当 FailOver 时，引擎会从源头重新发送消息进行重算，多次计算可能会产生的不一致的结果，但由于「Strong Production」会对计算进行去重，因此即便进行了多次重算，但有且仅有一次重算的结果被输出给下游（下游算子或结果接受端），从整体上来看数据是满足一致性的，这也被称之为「Effective Determinism」。

MillWheel 会对每一条记录赋予一个唯一 ID，同时基于此 ID 维护一份是否处理过当前记录的目录。对于每一条流入当前算子的记录，引擎查找此 ID 目录以确定此记录是否是已经处理过。这里会有很多技术上的挑战，这里稍微举几个例子。

譬如，需要有稳定且高吞吐的存储后端用于结果存储，Google 内部的 BigTable 发挥了其作用。流任务执行前后，引擎会对执行流做若干优化，如合并多个逻辑算子至单个算子（类似 Flink 中的 chain 化）、节点内先执行部分合并（count / sum）后再 shuffle等等，种种手段均是为了降低算子间 IO 的数据规模。

此外，在判断「当前记录」是否已被处理时，MillWheel 使用了布隆过滤器用于前置过滤，因为在一个正常运行的流计算任务中，记录绝大多数的时间都是不重复的，这刚好契合布隆过滤器的使用场景（如过滤器返回不存在则记录一定不存在），引擎中的每个节点都维护了以记录 ID 为主键的布隆过滤器，计算前都会通过此过滤器进行判断，若提示不存在则进行数据处理，如果存在，则需要二次校验。当然，MillWheel 在实际使用布隆过滤器，是做了若干改造的，这里就不具体展开了。

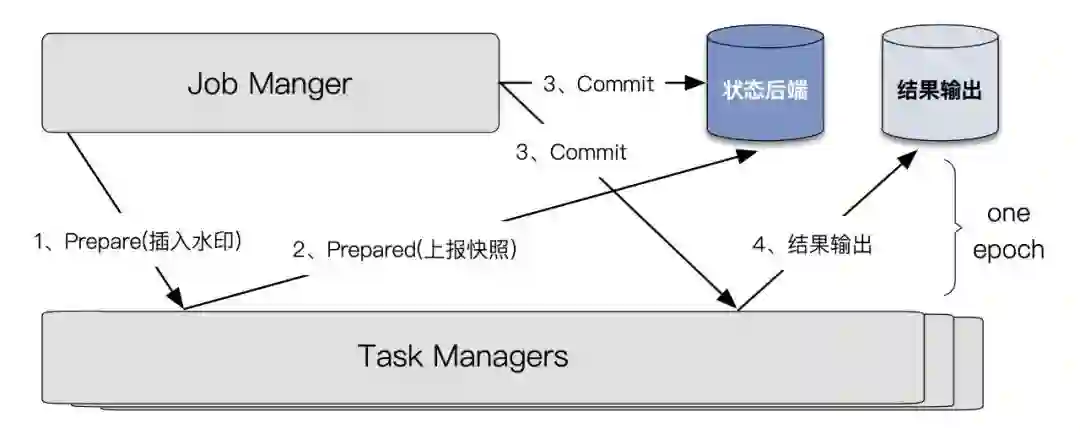
2 Apache Flink

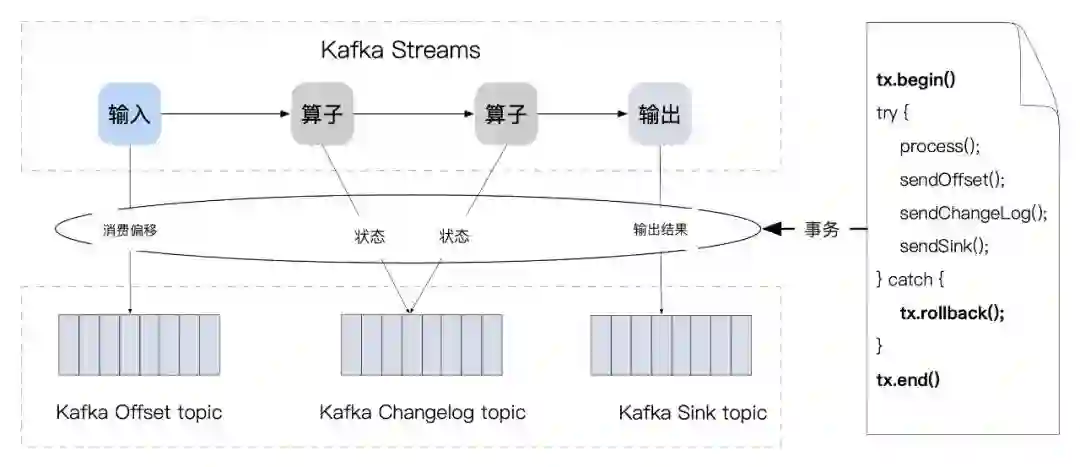
MillWheel 作为一个内部系统可以存储每一个中间结果，但是对于开源系统的 Apache Flink 来说，毕竟不是每一个公司都有这么完备的技术基建。Flink 会定期把结果以事务的方式进行批量存储，这里的「结果」如上面分析，由源状态 SourceState(t)、算子状态 OperatorState(t) 、输出的结果 Sink(t) 组成，其中 Flink 把源状态和算子状态进行了打包，统称为「分布式一致性快照」（基于 Chandy-Lamport 分布式快照算法来实现），数据会持久化在 RocksDB 中。

如上图所示，Flink 引擎会定时（每个周期称之为一个 epoch）以 2PC 的方式提交结果。事实上，即便不考虑结果输出，Flink 「分布式一致性快照」的快照的实现也是一个 2PC 的过程：算子的状态快照存储类似于 2PC 的 Prepare 阶段，但 Commit 的确认仅需 Coordinator（ Flink JobManager）根据「是否收到了完整算子的 ACK 」来推出是否 Commit 或 Abort。将结果输出纳入快照生成的 2PC 后，端到端一致性数据处理语义的充分必要条件在这里也得到了满足：在流计算过程中，定期（epoch）以事务（2PC）的方式进行批量存储结果（分布式一致性快照 + 写外部存储）。需要注意的是，由于 Flink 会以 epoch 为周期输出结果，因此基于此构建的流处理系统会存在一定的端到端延迟。

3 Apache Kafka Streams

Kafka Streams 是 Apache Kafka 0.10.0版本中包含的一个Java库，严格来讲并不算一个完整的流处理引擎，利用这个库，用户可以基于 Kafka 构建有状态的实时数据处理应用，更进一步地，Kafka Streams 需要数据输入源和输出均为 Kafka 消息队列。

Kafka Streams 中的「结果」也以事务的方式批量持久化，但和 Flink 不同的是，这些结果是被写入不同的消息队列中：

源状态 SourceState(t)：即 Kafka 源中的 Offset 信息，会被写入一个单独的 Kafaka 队列中，该队列对用户透明；
算子状态 OperatorState(t) ：计算中算子的 Changelog，也会写入单独的 Kafaka 队列中，该队列对用户透明；
输出结果 Sink(t) ：即用户配置的实际的输出队列，用于存放计算结果。

Kafka Streams 将上述结果定期以事务的方式进行批量存储，上述事务在 Kafka 这被称之为 Transactions API，使用这个 API 构建的流处理应用，可以在一个事务中将多个主题消息进行同时提交，如果事务终止或回滚，则下游消费不会读取到相应的结果（当然下游消费者也需要配置相应的一致性级别），其过程如下图所示：

如果稍微回顾一下 Flink 一致性的实现逻辑，会发现这两者有很多相似点，因此 Kafka Streams 的输出结果也会存在一定的端到端延迟。因为在提交结果时创建了新的事务，所以平均事务大小由提交间隔确定，当流量相同时，较短的提交间隔将导致较小的事务，但太小的间隔将导致吞吐下降，因此吞吐量与端到端处理延迟之间需要有一个折衷。

同时，我们需要注意到的是，Flink 和 Kafaka 中的「事务」提交，和我们常规的操作关系型数据库中的事务还是有所不同的，后者的事务提交对象一般就一个（e.g. MySQL Server），但在流计算中，由于结果有下游输出、消费进度、算子状态等，因此流计算引擎需要设计一个全局的事务协议用于和下游待提交的各个存储后端进行交互。举例：Kafka Streams 的输出后端需要是 Kafka，以配合在事务提交过程中，屏蔽部分已输出至下游（被 Kafka Broker 持久化），但还不满足事务隔离性的消息（read_committed 级别），从流计算输出的角度来看，这些消息已被成功处理同时输出至下游，但从端到端的一致性来看，它们依然属于不一致的数据。又如，使用 Flink 处理 CDC（Change Data Capture）的场景，如果下游是 MySQL，在 Flink 2PC 完成之前，来自不同 Flink 节点的数据输出后其实已经被 commit，类似 Kafka Broker 中的消息无法撤回，MySQL 提交的事务也无法回滚，因此输出数据中也需要有类似的字段实现隔离（isolation）语义，以屏蔽这种不一致的数据。

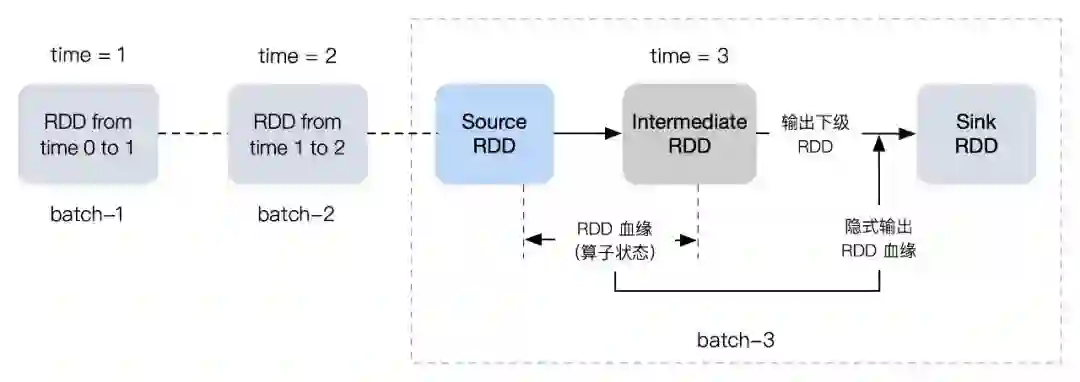
4 Apache Spark Streaming

这里提到的 Spark Streaming 指的是原始的基于「Micro-batch，微批」的 Spark 流处理引擎，后面 Spark 又提出了Structured Streaming，使用 Continuous Processing mode 来替代「微批」解决延迟的问题，容错机制上和 Flink 一样也使用了Chandy-Lamport 算法，Structured Stream 目前还不成熟，暂时还不能完全支持 Exactly-Once-Processing，因此这里着重对比 Spark Streaming。

Spark Streaming 只能保证引擎内部的处理逻辑是一致的，但是对于结果输出，则并没有做特别的抽象，因此如果我们希望实现端到端的一致性语义，则需要对自行维护和判断一些信息。同传统的批处理系统类似，流处理中也是以 RDD 构建出整个的数据血缘，当发生 FailOver 时，则重新计算整个 RDD 就可以了。如果 Spark Streaming 存在非确定性的计算，则不能实现端到端一致，原因是：1、不满足条件一「实时存储每一条结果」。如果能记录下每个 RDD 分区下的执行情况，避免重复执行（幂等），也一定程度上能实现端到端一致，但这需要进行大量的改造工作，最终形态会和 MillWheel 比较类似；2、不满足条件二「事务方式存储」，需要保证每个 RDD 产出环节的事务性（如最终结果写 HDFS 就不是原子的）。

考虑一种比较简单的场景：不存在非确定计算的流计算应用。如果不存在非确定计算，根据端到端的一致性语义的充分必要条件，只需要接受端实现幂等，则 Spark Streaming 就可以实现端到端的一致性。背后的原因是，当将形式化的结果定义与 Spark Streaming 进行映射，会发现当以「微批」的形式存储结果时，源状态和算子状态以 RDD 血缘的方式天然地和输出结果进行了绑定，即当输出最终结果时，我们其实也一并输出了源和算子状态，操作符合一致性条件。

更进一步，当把仅有确定性计算（幂等输出）的 Spark Streaming 和仅有确定性计算（幂等输出）的的 Flink 进行对比时，会发现二者非常相似。RDD 血缘类比分布式一致性快照，批量输出类比一致性快照后的结果输出，微批类比 epoch。不同之处在于：1、Spark Streaming 在计算过程中的每一个 RDD 生成阶段都会有延迟，而 Flink 在计算过程中可以进行实时处理；2、Spark Streaming 只有一个「epoch」，而 Flink 可以有多个「epoch」并行存在。基于上述两点原因，Flink 的数据处理的端到端延迟要小得多，但这两种引擎幂等输出能实现一致性的本质是相似的。

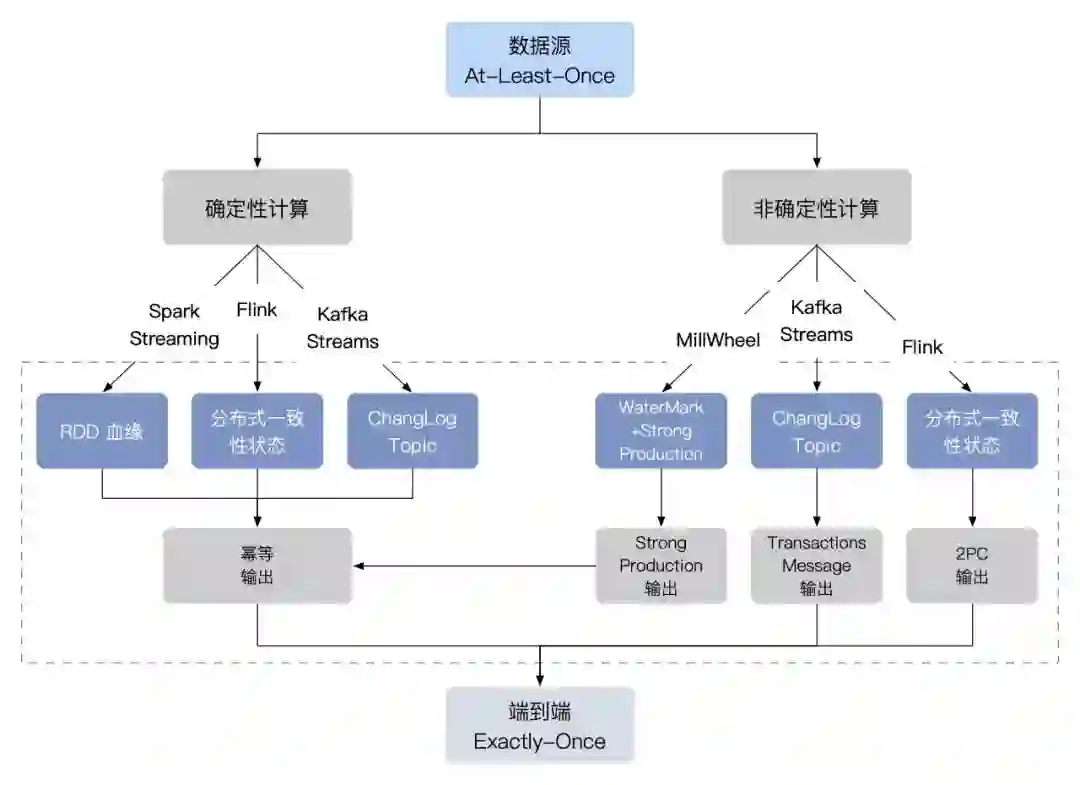
5 各引擎一致性实现总结

上面我们简述了目前主流的几种流计算引擎的一致性实现机制。从整体来看，如果实现端到端的一致性，则均需要满足我们上面从形式化定义推导出来的充分必要条件：实时存储每一条中间和最终计算结果，如果考虑吞吐率不能存储每一条，则需定期以事务的方式进行批量存储，这里的结果包含流计算引擎中的状态。上面的充分必要条件还可以进一步简化，即实时存储结果或定期事务，均可以视为当前处理逻辑单元（算子或最终存储）对上游的输入（引擎状态+输出结果）进行的幂等化处理：引擎 FailOver -> 输入源的事件会进行重发 -> 前期存储的结果会用于去重/事务回滚让结果（引擎状态+输出结果）回到上一次的一致性状态 -> 下一批结果输出 -> 结果接受端只影响一次 -> 实现了端到端的一致。

下面的图列举出各引擎实现端到端一致性的路线图：

前面分析端到端一致性的实现中，重点在分析引擎处理（算子）和输出端行为，没有提及对数据源的要求，数据源需具备重播（repaly）和消息去重的功能即可，属于基础要求，这里不再展开。

五总结与展望

本文从流计算的本质出发，推导出了在流处理中实现端到端一致性的通用解法，同时结合通用解法，分析了目前几种主流流计算引擎在一致性上的实现思路。有「财大气粗」型的 Google MillWheel，背靠强大的基础架构用于状态管理；有「心灵手巧」型的 Apache Flink，巧妙地结合了分布式一致性快照和两阶段事务实现一致性；也有「重剑无锋」型的 Apache Kafka Streams，直接将流处理过程事务化，屏蔽复杂的底层逻辑，编程模型和理解成本都更简单（当然也一定程度上限制其使用的场景）；也有「蓬勃发展」中的 Apache Spark （Structured）Streaming，底层的一些实现构想和 Apache Flink 愈加趋同，可以期待它将来能达到类似 Apache Spark 在批处理流域中的地位。

当然，引擎虽然这么多，但其背后是有若干条主线贯穿的，希望我们能拨开迷雾，不被营销的噱头所影响，能洞察到一些更为本质的东西。本文论述的端到端一致的流数据处理实现，重点聚焦在「计算和状态」管理，但实际上，还有很多因素需要我们去考虑，如时间窗口的推导、延迟数据的处理策略、底层计算节点的通信容错等，这些问题多多少少也会影响数据的一致性，考虑到文中篇幅，这里就不一一展开了，感兴趣的同学可以选择一个主题做深入研究。

下面这些论文对进一步了解流计算很有帮助，感兴趣的同学可以参考：

《Streaming System》，T Akidau, S Chernyak, R Lax
《Transactions in Apache Kafka》，Apurva Mehta，Jason Gustafson
《A Survey of State Management in Big Data Processing Systems》，QC To, J Soto, V Markl
《MillWheel: fault-tolerant stream processing at Internet scale》，T Akidau, A Balikov, K Bekiroğlu, S Chernyak
《Discretized Streams: Fault-Tolerant Streaming Computation at Scale》，M Zaharia, T Das, H Li, T Hunter