【泡泡图灵智库】对前馈神经网络学习难点的数学理解

会员服务 ·

【泡泡图灵智库】对前馈神经网络学习难点的数学理解

2018 年 7 月 9 日 泡泡机器人SLAM

泡泡图灵智库，带你精读机器人顶级会议文章

标题：Towards a Mathematical Understanding of the Difficulty in Learning with Feedforward Neural Networks

作者：Hao Shen

来源：CVPR 2018

播音员：四姑娘

编译：张博

审核：彭锐

欢迎个人转发朋友圈；其他机构或自媒体如需转载，后台留言申请授权

摘要

大家好，今天为大家带来的文章是——对前馈神经网络学习难点的数学理解，该文章发表于CVPR 2018。

训练深度神经网络用于解决机器学习问题是该领域的一大挑战，主要是由于其相关的优化问题是高度非凸的。最近发现表明许多训练算法得到的是局部极小值，导致花费了巨大努力去寻求数学解释。本文工作从平滑优化的角度来理解这项挑战。通过设定有限样本的精确学习，通过临界点分析确定全局极小值的充分条件是局部最小值。此外，将比较优秀的算法如Generalised Gauss Newton（GGN）算法，严格地重新定义为近似牛顿算法，它在精确学习的条件下具有局部二次收敛到全局最小值的性质。

主要贡献

1. 在精确学习的条件下，刻画了全损失函数的临界点条件，并研究了保证局部最小值是全局极小值的充分条件。

2.采用广义高斯牛顿算法，具有局部二次收敛到全局最小值的性质。

算法流程

图1 有监督学习的近似牛顿算法

第一步：对多层感知机输入T个样本计算并计算l层输出以及导数。

第二步：(1)计算本文构建的矩阵序列 (2)通过对角矩阵与哈密顿算子计算l层的权重参数 (3)计算误差函数海森矩阵。

第三步：由L层到1层，样本1到T计算(1)前向逐层计算构建矩阵(2)计算逐层的权重参数。

第四步：L层到1层计算损失函数梯度。

第五步：通过本文公式37计算近似损失函数海森矩阵。

第六步：计算牛顿更新权重。

第七步：从步骤一重复直到收敛。

主要结果

文章主要结果：

在四个区域分类基准测试算法。正方形区域内通过3个半径分别为1，2，3的同心圆分割成4个区域。对应类别1，2，3，4进行训练。

1. 隐含层误差函数为平方损失函数。通过20组随机抽取样本进行随机初始化权重运算。

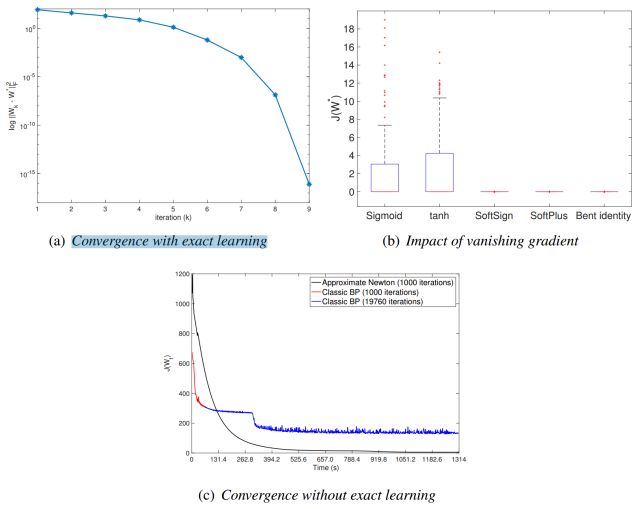
图2 近似牛顿算法的研究，即广义高斯牛顿算法。(a)精确学习收敛性 (b)消失梯度的影响 (c)无精确学习的收敛性

2. 进一步研究了应用五种不同激活函数的性能，Sigmoid,tanh,SoftSign,SoftPlus与Bent identity,如图2(b)。

3. 与经典的BP算法进行对比，假设不通过精确学习，步长为0.01，并进行1000次迭代情况下AN/GGN每次迭代的运行时间约为BP迭代的21.4倍。如图2(c)所示，BP的前1000次迭代用红色突出显示，其余的迭代用蓝色显示。AN/GGN在开始时上升，然后平稳收敛到全局极小值，而BP则表现出强振荡。

Abstract

Training deep neural networks for solving machine learning problems is one great challenge in the field, mainly due to its associated optimisation problem being highly non-convex. Recent developments have suggested that many training algorithms do not suffer from undesired local minima under certain scenario, and consequently led to great efforts in pursuing mathematical explanations for such
observations. This work provides an alternative mathematical understanding of the challenge from a smooth optimisation perspective. By assuming exact learning of finite samples, sufficient conditions are identified via a critical point analysis to ensure any local minimum to be globally minimal as well. Furthermore, a state of the art algorithm, known as the Generalised Gauss-Newton (GGN) algorithm,
is rigorously revisited as an approximate Newton’s algorithm, which shares the property of being locally quadratically convergent to a global minimum under the condition of exact learning.

如果你对本文感兴趣，想要下载完整文章进行阅读，可以关注【泡泡机器人SLAM】公众号。

点击阅读原文，即可获取本文下载链接。

欢迎来到泡泡论坛，这里有大牛为你解答关于SLAM的任何疑惑。

有想问的问题，或者想刷帖回答问题，泡泡论坛欢迎你！

泡泡网站：www.paopaorobot.org

泡泡论坛：http://paopaorobot.org/forums/