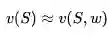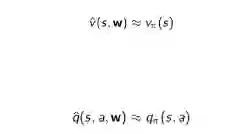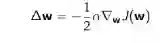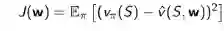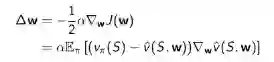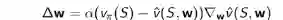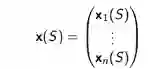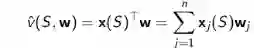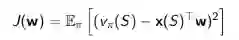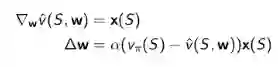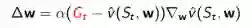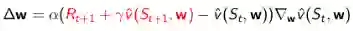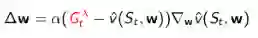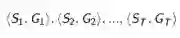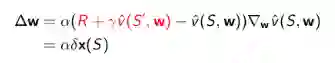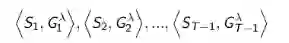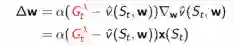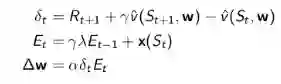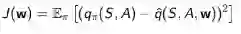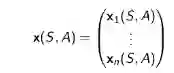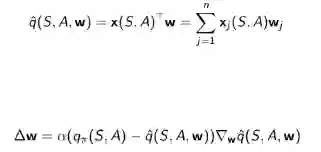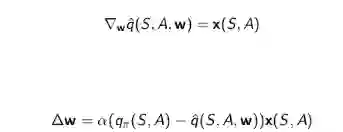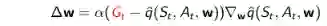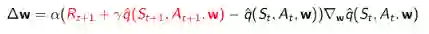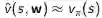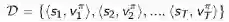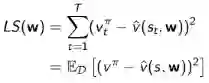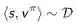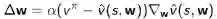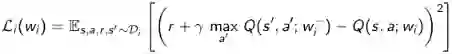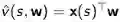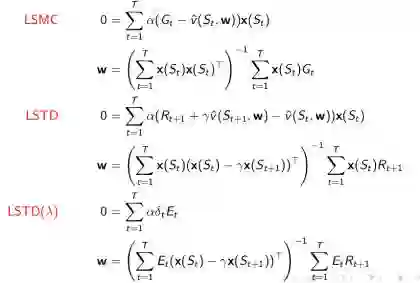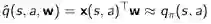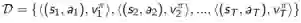【AlphaGo Zero 核心技术-深度强化学习教程笔记06】价值函数的近似表示

2017 年 10 月 26 日 专知叶强

点击上方“专知”关注获取更多AI知识!

【导读】Google DeepMind在Nature上发表最新论文，介绍了迄今最强最新的版本AlphaGo Zero，不使用人类先验知识，使用纯强化学习，将价值网络和策略网络整合为一个架构，3天训练后就以100比0击败了上一版本的AlphaGo。Alpha Zero的背后核心技术是深度强化学习，为此，专知有幸邀请到叶强博士根据DeepMind AlphaGo的研究人员David Silver《深度强化学习》视频公开课进行创作的中文学习笔记，在专知发布推荐给大家！（关注专知公众号，获取强化学习pdf资料，详情文章末尾查看！）

叶博士创作的David Silver的《强化学习》学习笔记包括以下：

笔记序言：【教程】AlphaGo Zero 核心技术 - David Silver深度强化学习课程中文学习笔记

《强化学习》第一讲简介
《强化学习》第二讲马尔科夫决策过程
《强化学习》第三讲动态规划寻找最优策略
《强化学习》第四讲不基于模型的预测
《强化学习》第五讲不基于模型的控制
《强化学习》第六讲价值函数的近似表示
《强化学习》第七讲策略梯度
《强化学习》第八讲整合学习与规划
《强化学习》第九讲探索与利用

以及包括也叶博士独家创作的强化学习实践系列！

强化学习实践一迭代法评估4*4方格世界下的随机策略
强化学习实践二理解gym的建模思想
强化学习实践三编写通用的格子世界环境类
强化学习实践四 Agent类和SARSA算法实现
强化学习实践五 SARSA(λ)算法实现
强化学习实践六给Agent添加记忆功能
强化学习实践七 DQN的实现

今天《强化学习》第六讲 价值函数的近似表示；

之前的内容都是讲解一些强化学习的基础理论，这些知识只能解决一些中小规模的问题，很多价值函数需要用一张大表来存储，获取某一状态或行为价值的时候通常需要一个查表操作（Table Lookup），这对于那些状态空间或行为空间很大的问题几乎无法求解，而许多实际问题都是这些拥有大量状态和行为空间的问题，因此只掌握了前面5讲内容，是无法较好的解决实际问题的。本讲开始的内容就主要针对如何解决实际问题。

本讲主要解决各种价值函数的近似表示和学习，下一讲则主要集中与策略相关的近似表示和学习。在实际应用中，对于状态和行为空间都比较大的情况下，精确获得各种v(S)和q(s,a)几乎是不可能的。这时候需要找到近似的函数，具体可以使用线性组合、神经网络以及其他方法来近似价值函数：

表示引入的参数，通常是一个矩阵或至少是一个向量。

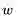
通过函数近似，可以用少量的参数w来拟合实际的各种价值函数。本讲同时在理论上比较了各种近似方法的优缺点以及是否收敛与最优解等。本讲将各种近似方法分为两大类，一类是“递增方法”，针对每一步，近似函数得到一些信息，立即优化近似函数，主要用于在线学习；另一类是“批方法”，针对一批历史数据集中进行近似。两类方法没有明显的界限，相互借鉴。

本节先讲解了引入价值函数的近似表示的重要性，接着从梯度开始讲起，使用梯度下降可以找到一个目标函数的极小值，以此设计一个目标函数来寻找近似价值函数的参数。有机器学习基础的读者理解本节会非常容易。本节的理论重点在于理解不同强化学习方法在应用不同类型的近似函数时的收敛性，能否获得全局最优解，以及DQN算法的设计思想及算法流程。本讲罗列了大量的数学公式，并以线性近似函数为例给出了具体的参数更新办法，这些公式在强大的机器学习库面前已经显得有些过时了，但对于理解一些理论还是有些帮助的。此外，在本讲的最后还简单介绍了不需要迭代更新直接求解线性近似函数参数的方法，可以作为补充了解。

简介 Introduction

大规模强化学习 Large-Scale Reinforcement Learning

强化学习可以用来解决大规模问题，例如围棋有个状态空间，控制直升机飞行需要的是一个连续状态空间。如何才能将强化学习应用到这类大规模的问题中，进而进行预测和控制呢？

近似价值函数 Value Function Approximation

到目前为止，我们使用的是查表（Table Lookup）的方式，这意味着每一个状态或者每一个状态行为对对应一个价值数据。对于大规模问题，这么做需要太多的内存来存储，而且有的时候针对每一个状态学习得到价值也是一个很慢的过程。

对于大规模问题，解决思路可以是这样的：

1. 通过函数近似来估计实际的价值函数：

2. 把从已知的状态学到的函数通用化推广至那些未碰到的状态中

3. 使用MC或TD学习来更新函数参数。

近似函数的类型 Types of Value Function Approximation

针对强化学习，近似函数根据输入和输出的不同，可以有以下三种架构：

1. 针对状态本身，输出这个状态的近似价值；

2. 针对状态行为对，输出状态行为对的近似价值；

3. 针对状态本身，输出一个向量，向量中的每一个元素是该状态下采取一种可能行为的价值。

有哪些近似函数 Which Function Approximator

所有和机器学习相关的一些算法都可以应用到强化学习中来，其中线性回归和神经网络在强化学习里应用得比较广泛，主要是考虑这两类方法是一个针对状态可导的近似函数。

强化学习应用的场景其数据通常是非静态、非独立均匀分布的，因为一个状态数据是可能是持续流入的，而且下一个状态通常与前一个状态是高度相关的。因此，我们需要一个适用于非静态、非独立均匀分布的数据的训练方法来得到近似函数。

注：iid: independent and identically distributed 独立和均匀分布

下文将分别从递增方法和批方法两个角度来讲解价值函数的近似方法，其主要思想都是梯度下降，与机器学习中的随机梯度下降和批梯度下降相对应。

递增方法 Incremental Methods

首选简要解释了下什么是梯度、梯度下降以及梯度下降能做什么。

梯度下降 Gradient Descent

假定J(w)是一个关于参数w的可微函数，定义J(w)的梯度如下：

调整参数超朝着负梯度的方向，寻找J(w)的局部最小值：

式中α是步长参数，机器学习里称为学习速率参数

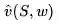
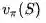
目标：找到参数向量w，最小化近似函数与实际函数的均方差：

梯度下降能够找到局部最小值：

使用随机梯度下降对梯度进行更新，来近似差的期望：

每一步，参数朝着实际的价值函数进行一定程度地逼近。

这里介绍了使用线性近似函数时具体的梯度下降公式：

线性函数近似——特征向量 Linear Function Approximation - Feature Vectors

用一个特征向量表示一个状态，每一个状态是由以w表示的不同强度的特征来线性组合得到：

可以通过对特征的线性求和来近似价值函数：

这样，我们的目标函数可以表示成：

使用随机梯度下降可以收敛至全局最优解。

参数更新规则相对比较简单：

即：参数更新量 = 步长 × 预测误差 × 特征值

“查表”方法是一个特殊的线性价值函数近似方法：每一个状态看成一个特征，个体具体处在某一个状态时，该状态特征取1，其余取0。参数的数目就是状态数，也就是每一个状态特征有一个参数，这比较简单，具体就不列公式了。

预测——递增算法 Incremental Prediction Algorithms

事实上，之前所列的公式都不能直接用于强化学习，因为公式里都有一个实际价值函数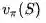，或者是一个具体的数值，而强化学习没有监督数据，因此不能直接使用上述公式。

强化学习里只有即时奖励，没有监督数据。我们要找到能替代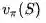的目标值，以便来使用监督学习的算法学习到近似函数的参数。

对于MC算法，目标值就是收获：

对于TD(0)，目标值就是TD目标：

对于TD(λ)，目标值是λ收获：

MC应用于状态价值函数近似

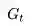
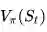
收获是真实价值的有噪声、无偏采样，可以把它看成是监督学习的标签数据带入机器学习算法进行学习，这样训练数据集可以是：

如果使用线性蒙特卡洛策略迭代，那么每次参数的修正值则为：

蒙特卡洛策略迭代即使使用线性函数近似时也是收敛至一个局部最优解。

TD应用于状态价值函数近似

TD目标值是真实价值的有噪声、有偏采样。此时的训练数据集是：

如果使用线性TD(0)学习，则有：

线性TD(0)近似收敛至全局最优解。

TD(λ)应用于状态价值函数近似

TD(λ)目标值是真实价值的有噪声、有偏采样。此时的训练数据集是：

如果使用线性TD(λ)学习，从前向认识看，有：

如果使用线性TD(λ)学习，从反向认识看，有：

对于一个完整的Episode，TD(λ)的前向认识和反向认识对于w的改变是等效的。

线性TD(0)近似收敛至全局最优解。

控制——递增算法

在上一讲里曾提到，使用强化学习进行不基于模型控制需要两个条件。如何把近似函数引入到控制过程中呢？我们需要能够近似状态行为对的价值函数近似而不是仅针对状态的价值函数近似。

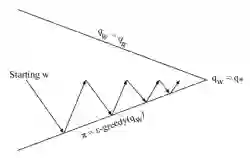
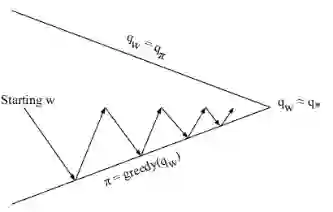
从一系列参数开始，得到一个近似的状态行为对价值函数，在Ɛ-greedy执行策略下产生一个行为，执行该行为得到一个即时奖励，以此数据计算目标值，进行近似函数参数的更新。再应用这个策略得到后续的状态和对应的目标值，每经历一次状态就更新依次参数，如此反复进行策略的优化，同时逼近最优价值函数。

策略评估：是一个近似策略评估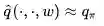，特别是早期误差会较大，而且这种近似无法最终收敛于最优策略对应的行为价值函数，只能在其周围震荡，后文将讲述改进方法。

策略改善：使用Ɛ-greedy执行。

行为价值函数近似表示为：

最小化均方差：

使用随机梯度下降来寻找局部最优解：

同样介绍了使用线性函数来近似状态行为价值函数时的公式，状态行为价值可以用特征向量表示：

如此，线性特征组合的状态行为价值近似函数可以表示为：

随机梯度下降更新参数：

线性控制算法

与预测算法类似，我们找到真实行为价值的目标值。

对于MC算法，目标值就是收获：

对于TD(0)，目标值就是TD目标：

对于前向认识TD(λ)，目标值是λ收获：

对于后向认识TD(λ)，对应的参数更新是：

示例——小车爬山

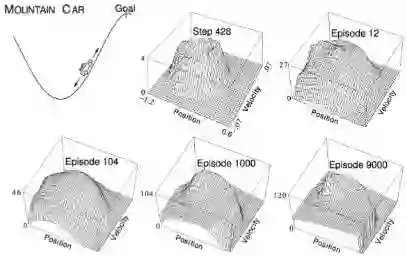
小车爬山是一个经典的强化学习示例。环境如图左上角所示，小车被困于山谷，单靠小车自身的动力是不足以在谷底由静止一次性冲上右侧目标位置的，比较现时的策略是，当小车加速上升到一定位置时，让小车回落，同时反向加速，使其加速冲向谷底，借助势能向动能的转化冲上目标位置。现在问题是在模型位置的情况下，如何用强化学习的方法找到小车冲上目标位置的最优策略。

状态空间是小车的位置和速度，其它几张三维图展示的是经过不同步数（上中图）以及不同Episode（其余几张三维图）的学习，小车位于某个位置同时具有某个速度的状态价值。在这个例子中，行为空间是离散的，只能选则正向的最大油门和反向的最大油门两个离散值。

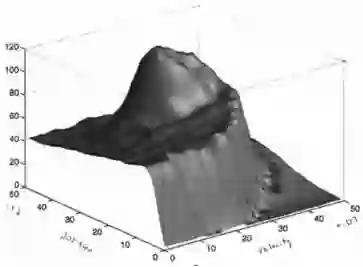
最后小车使用SARSA学习到了接近最优策略的价值函数，如下图：

个人体会：实际上这里没有显示状态行为价值图，主要是因为行为空间是一维2个离散变量，在任何一个状态，两个行为中只有一个行为是有正向价值的，另一个则是负向价值的。因此根据Bellman最优方程，状态空间价值总选择正向行为价值的那个数值。

关于λ——需要Bootstrap吗？

下图显示了几种不同的任务，使用不同λ进行的强化学习算法分析结果。总的来说λ=1的时候通常算法表现是很差的，TD(0)是比MC好得多的方法，这说明了Bootstrap的重要性；不同的任务对应的最优λ值是不太容易确定的。

收敛性

预测学习

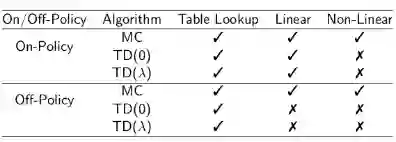
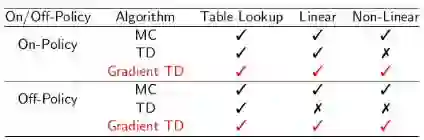
MC使用的是实际价值的有噪声无偏估计，虽然很多时候表现很差，但总能收敛至局部或全局最优解。TD性能通常更加优秀，是否意味着TD也是一直收敛的呢？答案是否定的。原讲义给出了一个TD学习不收敛的例子，这里不再详述，这里给出各种算法在使用不同近似函数进行预测学习时是否收敛的小结：

注：打钩表示能收敛，打叉表示不收敛。

从表中可以看出，没有函数近似时，各种算法都收敛；线性函数近似时现时策略学习可以收敛，但离线策略时仅有MC收敛；非线性函数近似时无论采用现时策略还是离线策略只有MC收敛。而MC算法在实际中是很少使用的。这给强化学习的实际应用带来的挑战。好在我们有一些改善TD算法的办法。

TD算法在更新参数时不遵循任何目标函数的梯度是导致它在离线策略或使用非线性近似函数可能会发散的原因，我们可以通过修改TD算法使得它遵循Projected Bellman Error的梯度进而收敛。视频及讲义没有具体讲解Gradient TD。

控制学习

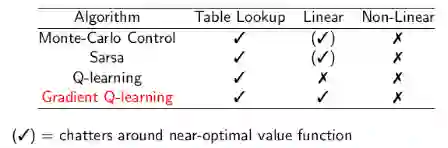
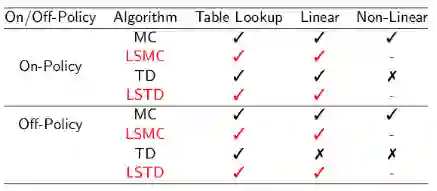
针对控制学习的算法，其收敛性比较如下图：

(√) 表示在最优价值函数附近震荡

针对控制学习算法，大多数都能得到较好的策略，但是理论上只要存在函数近似，就都不是严格收敛的，比较常见的是在最优策略上下震荡，逐渐逼近然后突然来一次发散，再逐渐逼近等。使用非线性函数近似的效果要比近似函数要差很多，实际也是如此。

批方法 Batch Methods

前面所说的递增算法都是基于数据流的，经历一步，更新算法后，我们就不再使用这步的数据了，这种算法简单，但有时候不够高效。与之相反，批方法则是把一段时期内的数据集中起来，通过学习来使得参数能较好地符合这段时期内所有的数据。这里的训练数据集“块”相当于个体的一段经验。

最小平方差预测

假设存在一个价值函数的近似：

以及一段时期的、包含<状态、价值>的经历D：

最小平方差算法要求找到参数w，使得下式值最小：

这就相当于经历重现（Experience Replay），把一段时期内的经历重新过一遍，更新参数。这种算法实现起来不是很难，只要重复：

1. 从经历中去除一个<s,v>：

2. 应用随机梯度下降来更新参数：

这将收敛至针对这段经历最小平方差的参数：

批方法应用于DQN网络

先前说过TD方法结合非线性的神经网络函数近似可能不会收敛，但DQN(Deep Q-Networks) 使用经历重现和固定的Q目标值能做到收敛而且保持很好的鲁棒性。在解释其收敛之前先要介绍DQN算法的要点：

1. 依据Ɛ-greedy执行策略产生t时刻的行为；

2. 将大量经历数据（例如百万级的）以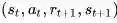存储在内存里，作为D大块；

3. 从D大块中随机抽取小块（例如64个样本数据）数据；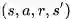

4. 维护两个神经网络DQN1，DQN2,一个网络固定参数专门用来产生目标值，目标值相当于标签数据。另一个网络专门用来评估策略，更新参数。

5. 优化关于Q网络和Q目标值之间的最小平方差：

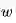
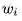
式中：在小块学习过程中是固定的，则是动态更新的参数。

6. 用随机梯度下降的方式更新参数。

首先，随机采样打破了状态之间的联系；第二个神经网络会暂时冻结参数，我们从冻结参数的网络而不是从正在更新参数的网络中获取目标值，这样增加了算法的稳定性。经过一次批计算后，把冻结参数的网络换成更新的参数再次冻结产生新一次迭代时要用的目标值。

这里举了一个应用DQN玩Atari类游戏的例子，算法直接对屏幕进行拍照，将最近4帧的屏幕图像送入一个卷积神经网络，最终输出针对游戏手柄的18个按钮精细方位的Q(s,a)值算法直接获取游戏屏幕的图像信息，对应的近似函数类型好像是第三类，奖励信息根据当时屏幕显示的分数确定。这种设计在50中Atari类游戏中测试，表现很好。具体可以参考原讲义图表。

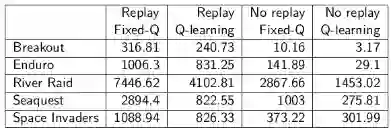
此外用了一张表比较了在DQN中有没有应用固定参数、以及有没有使用经历重现（批方法）两个条件时在5款游戏中的表现，结果体现了这两个条件联合应用的优势：

批方法的直接计算

通过比较发现使用批方法能够找到最小平方差的解决方案，提高算法的稳定性，但是它需要多次迭代。我们可以设计一个价值函数的线性近似函数：

然后直接求解参数。求解思路是逆向思维，假设已经找到这个参数，那么他应该满足最小LS(w)，通过把LS展开，可以直接得到w：

这种方法直接求解的时间复杂度是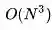，使用Shermann-Morrison法求解复杂度是

，n是特征数量，这意味着求解该问题的难度与设计的特征数量多少有关，而与状态空间大小无关，因此适合应用与那些特征较少的问题。

将这种方法分别应用于MC, TD, 和TD()学习方法，就分别得到LSMC, LSTD, 和LSTD(λ)。结合之前的各种价值函数的近似这里直接贴上w求解公式：

下图展示了各种方法的收敛性比较：

最小平方差控制

使用最小平房差进行策略迭代的原理和结局如图所示：

策略评估使用最小平方差Q学习，策略改善使用：Greedy 搜索策略。如果使用最小平方差方法进行策略控制，我们必须要设计针对行为价值函数的线性近似：

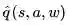
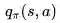
使用下列经历，最小化和的平方差：

对于策略评估我们希望改善策略，使用类似Q学习的方法，进行离线策略学习。

（这其中有不少内容，视频因时间原因跳过了）

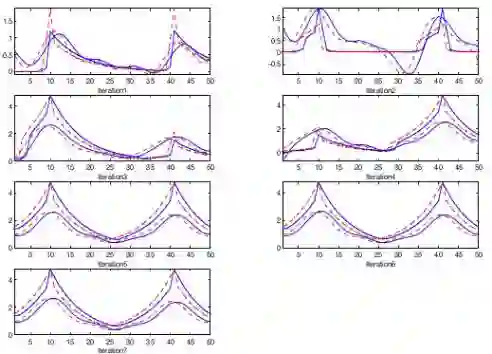
最后举了一个水平随机行走的例子，这个例子比之前的随机行走要复杂，状态空间扩展为50个，但可以仅分为两类：状态10和41是两个好的状态，获得奖励1；其他状态均获得奖励0。最优策略是：当个体处在1-9这9个状态时采取向右移步的行为，用R(1-9)表示，在其他状态时的最有行为分别是：L(10-25)，R(26-41)，和L(42-50)。

算法使用的特征是：针对每一个行为（左或右）设计10个均匀分布的高斯分布状态特征。

下图解释了LSPI算法能在少数几次迭代过后就找到了每个状态的状态价值函数，也就最优策略。红、蓝色分别代表左右不同的行为对应的价值。关于该示例的详细介绍参考原讲义内容。