【泡泡点云时空】AA-ICP:一种基于Anderson加速的最近邻点迭代方法(ICRA-2)

会员服务 ·

【泡泡点云时空】AA-ICP:一种基于Anderson加速的最近邻点迭代方法(ICRA-2)

2018 年 9 月 16 日 泡泡机器人SLAM

泡泡点云时空，带你精读点云领域顶级会议文章

标题：AA-ICP:一种基于Anderson加速的最近邻点迭代方法

作者：Artem L. Pavlov，Grigory V. Ovchinnikov，Dmitry Yu. Derbyshev，Dzmitry Tsetserukou，Ivan V. Oseledets

来源：ICRA 2018

音频：程枭、黄凯

编译：黄玉玺、李永飞

审核：郑英林

欢迎个人转发朋友圈；其他机构或自媒体如需转载，后台留言申请授权

摘要

最近邻点迭代（ICP）是一种广泛应用的配准方法。尽管该方法非常简单又鲁棒，但是需要较高的计算代价，这对于计算资源有限的平台来说，很难实现实时性。本文中，我们提出了一种新颖有效的方法加速ICP，并且不需要对现有的代码做大量的修改。

该方法基于Anderson加速的思想，这是一个搜索压缩映射固定点的迭代过程。该方法与Picard迭代法相比通常速度更快（Picard迭代法是ICP实现中常用的方法）。ICP作为一个固定点问题，可以通过启发式的方法在保证快速性的同时改善整体的鲁棒性（因为原始的Anderson 加速对非压缩映射不鲁棒）。我们已经将本文的实现加入了PCL中，并在网上公开。通过对真实的数据测试充分验证了我们的说法。

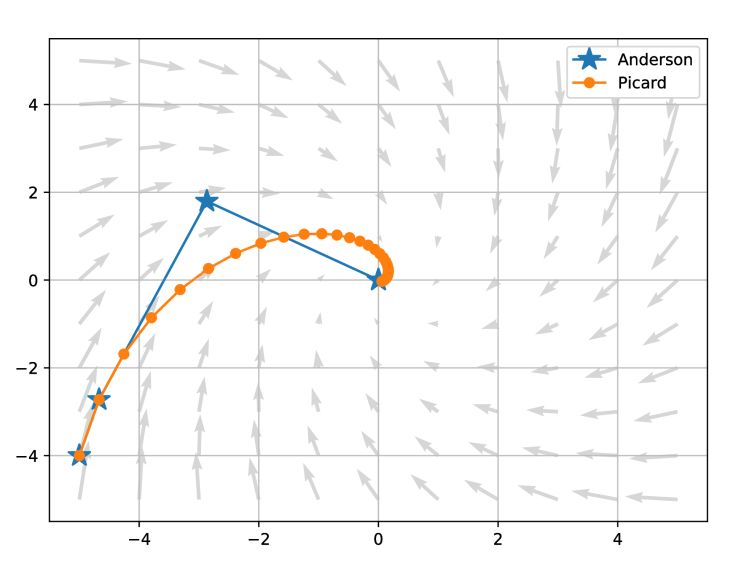
图1：对于二维映射G(u)=Au，Picard迭代与Anderson acceleration方法的对比。二者都是以（-5,-4）为起点迭代。星与圆都代表迭代点，灰色箭头代表在不同点的映射关系。

图2：Anderson acceleration算法流程。从上述流程中可以看到第n+1次的结果不仅仅与第n次的结果相关，而且与前面计算出来的所有的结果相关，因此其结果具有“跳跃性”，从而可以使其更快速的收敛。

图3：AA-ICP算法流程。为了弥补Anderson加速法在非压缩映射时的不稳定性，作者提出两个启发式的约束：

（1）当前的ICP误差不能显著大于前一次迭代的ICP误差，如果发生上述情况，将当前的结果视为无效，剔除迭代的序列。

（2）所有的权值αj必须处于一定范围内，同时α0 > 0，以保证新的点和最近一次迭代的趋势一致。

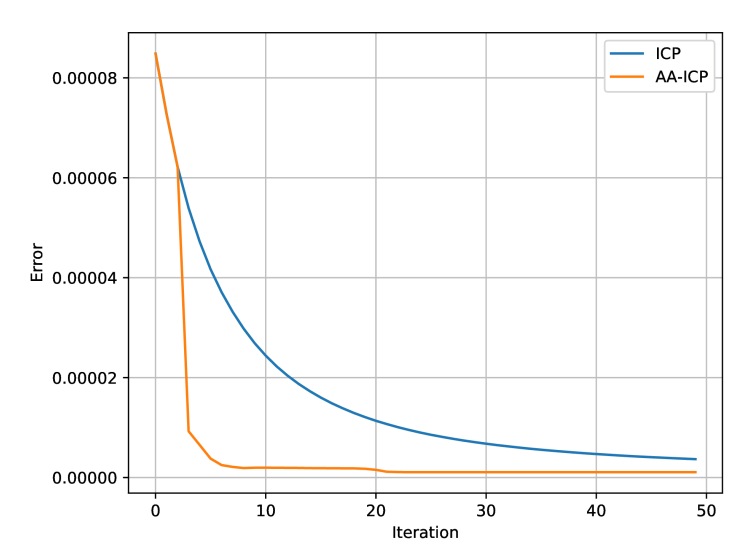
图4：ICP与AA-ICP随着迭代次数的增加，误差的变化

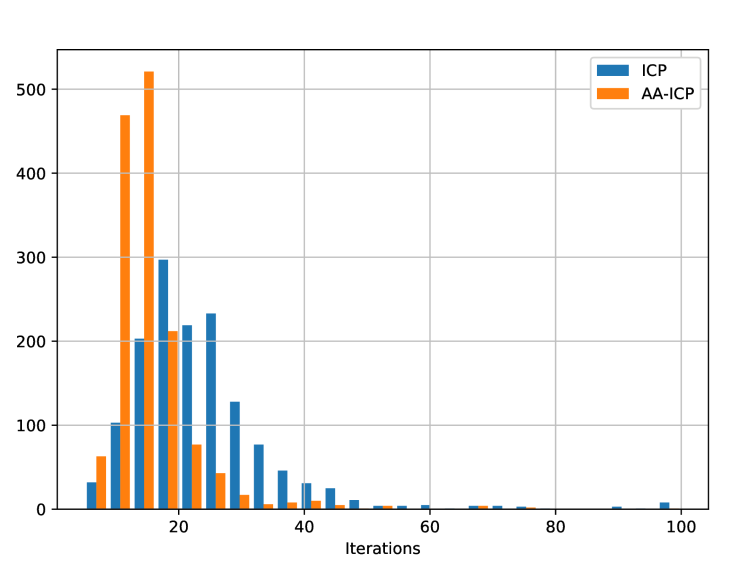
图5：ICP与AA-ICP收敛迭代次数直方图统计。从图中可以看到AA-ICP大部分在10次～30次以内可以收敛。

Abstract

Iterative Closest Point (ICP) is a widely used method for performing scan-matching and registration. Being simple and robust, this method is still computationally expensive and may be challenging to use in real-time applications with limited resources on mobile platforms. In this paper we propose a novel effective method for acceleration of ICP which does not require substantial modifications to the existing code. This method is based on an idea of Anderson acceleration which is an iterative procedure for finding a fixed point of contractive mapping. The latter is often faster than a standard Picard iteration, usually used in ICP implementations. We show that ICP, being a fixed point problem, can be significantly accelerated by this method enhanced by heuristics to improve overall robustness. We implement proposed approach into Point Cloud Library (PCL) and make it available online. Benchmarking on the real-world data fully supports our claims.

如果你对本文感兴趣，想要下载完整文章进行阅读，可以关注【泡泡机器人SLAM】公众号。

欢迎来到泡泡论坛，这里有大牛为你解答关于SLAM的任何疑惑。

有想问的问题，或者想刷帖回答问题，泡泡论坛欢迎你！

泡泡网站：www.paopaorobot.org

泡泡论坛：http://paopaorobot.org/forums/