海量文本用 Simhash， 2小时变4秒！ | 文本分析：大规模文本处理（2）

会员服务 ·

海量文本用 Simhash， 2小时变4秒！ | 文本分析：大规模文本处理（2）

2018 年 8 月 2 日 数说工作室

文本分析系列：

本文要解决的是这样一个问题：

有一段文本线索：

“延安西路921号，进门左边第三棵树，有一个一百三十年前的......”

我想从一个亿级数据库里，把包含这段线索的相似文本都捞出来，找到它背后更多的故事。

这是一个相似匹配的问题（文本相似匹配基础→ 词频与余弦相似度）。但是，亿级数据库，用传统的相似度计算方法太慢了，我们需要一个文本查询方法，可以快速的把一段文本的相似文本查出来。

在实际的文本处理工作中，不解决海量查询这一基本问题，耗时等待是非常可怕的。比如我们时常要对海量相似文本进行去重、或者对海量相似文本的聚类等。

具体场景为：在搜索引擎中查询一段文本，10分钟后才能返回？对微博上某种近一周的文本进行聚类，要等1个月？（说到聚类，效果好一点的聚类方法如DBSCAN，时间复杂度很高，耗时是非常让人绝望的，这个后续还会介绍）。

你会发现，很多时候，如果不先解决掉大规模相似文本的问题，后面很多高大上的分析、模型都做不了，这也是为什么我文本分析这个系列中，我先介绍“大规模文本处理”，而没有先介绍word2vec、LSTM等方法的原因。

在前面的文章里（→哈希函数），我们介绍过一种叫哈希函数的东西，他可以把文本转换成一段哈希指纹。从而对文本进行量化降维。但是，我们希望转换之后，相似的文本还能保持相似，比如 “最美数说君”，hash之后是 12345，“最帅数说君”，hash之后是12346，还能保持差不多的相似。这个是最难的，满足这种特性的hash函数，叫做局部敏感性哈希（LSH）。

本文要介绍的SimHash，就是其中的一种，谷歌就是用它来对海量文本进行去重。

一、SimHash原理

1、Simhash的使用

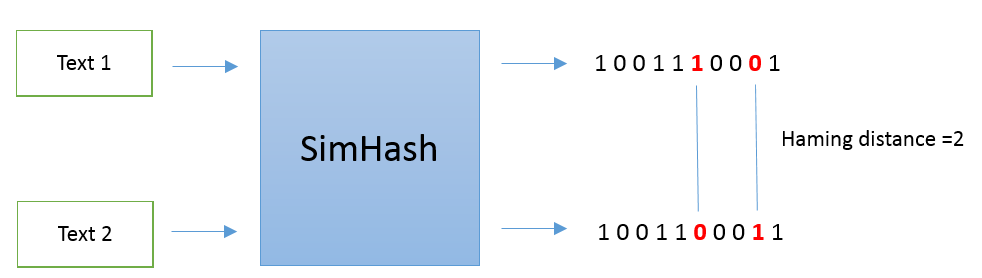
Simahash方法最早由Moses Charikar在《similarity estimation techniques from rounding algorithms》一文中提出。SimHash是将一段文本hash成一串二进制的指纹（如0010110），然后配用海明距离进行两两文本的比较。海明距离，说白了就是看两段二进制指纹有多少不一样，具体可以看这里→ 常用距离/相似度一览。流程如下图所示：

一般来说，如果海明距离小于3，则认为这两个文本是相似文本。那么SimHash是如何计算的呢？

2、Simhash 的计算

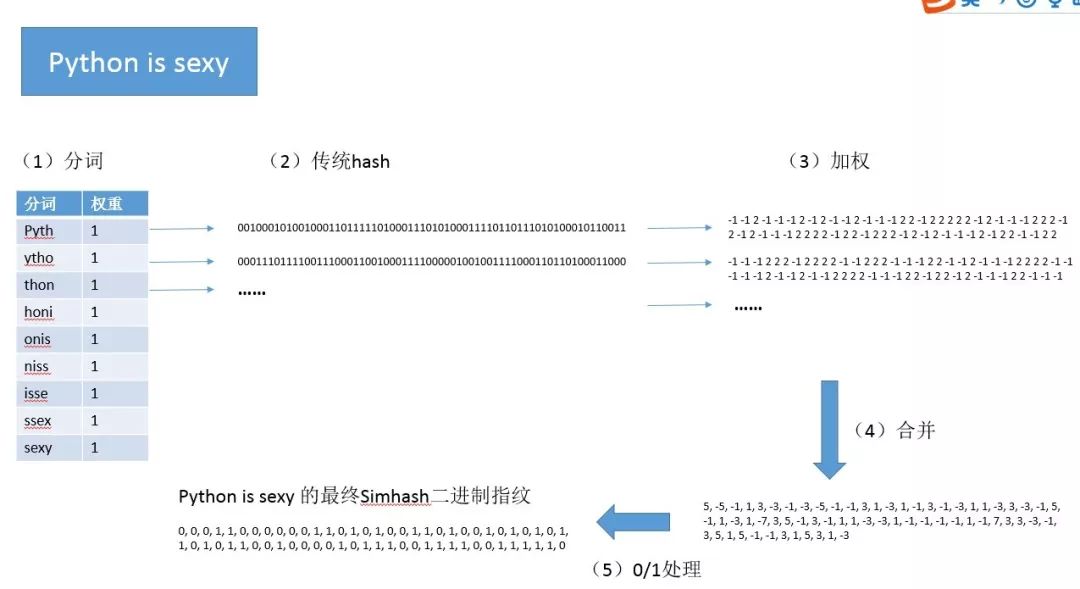
我们以 “Python is sexy” 为例，展示以下一段文本的SimHash过程：

先给一个总的流程图：

（1）分词、给定权重

首先是分词，且给定每一个词的权重。

这里我们采用四字母为单位来切词（我们把大小写归一化、空格去掉），权重统一为1：

[Pyth：1, ytho：1, thon：1, honi：1, onis：1, niss：1, isse：1, ssex：1, sexy：1]

（2）传统hash

把每一个词用传统方法hash成数字（即 hashcode），这里位数根据存储成本和数据集大小来选取，一般多选64位：

Pyth：

0010001010010001101111101000111010100011110110111010100010110011

ytho：

0001110111100111000110010001111000001001001111000110110100011000

......

（3）加权

每一个分词的 hashcode 中，对应位上如果为1，则该位加上权重w，这里权重为1，即+1,；对应位上如果不为1，则该位减去权重w，这里即-1。

Pyth：

-1 -1 2 -1 -1 -1 2 -1 2 -1 -1 2 -1 -1 -1 2 2 -1 2 2 2 2 2 -1 2 -1 -1 -1 2 2 2 -1 2 -1 2 -1 -1 -1 2 2 2 2 -1 2 2 -1 2 2 2 -1 2 -1 2 -1 -1 -1 2 -1 2 2 -1 -1 2 2

ytho：

-1 -1 -1 2 2 2 -1 2 2 2 2 -1 -1 2 2 2 -1 -1 -1 2 2 -1 -1 2 -1 -1 -1 2 2 2 2 -1 -1 -1 -1 -1 2 -1 -1 2 -1 -1 2 2 2 2 -1 -1 -1 2 2 -1 2 2 -1 2 -1 -1 -1 2 2 -1 -1 -1

......

（4）合并

现在每个分词都有64位的二进制表示，我们将每一位进行纵向累加，也就是将每个分词的第1位累加，得到总的第1位，每个分词的第2位累加，得到总的第2位，同理第3位、第4位......第64位。最终得到了一个总的64位的二进制表示：

Python is sexy：

-5, -5, -1, 1, 3, -3, -1, -3, -5, -1, -1, 3, 1, -3, 1, -1, 3, -1, -3, 1, 1, -3, 3, -3, -1, 5, -1, 1, -3, 1, -7, 3, 5, -1, 3, -1, 1, 1, -3, -3, 1, -1, -1, -1, -1, 1, -1, 7, 3, 3, -3, -1, 3, 5, 1, 5, -1, -1, 3, 1, 5, 3, 1, -3

（5）0/1处理

对于64位的每一位，如果大于0，则赋值为1，否则为0：

Python is sexy 的最终 simhash 二进制指纹：

0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0

以上，就是一段文本的Simhash过程。它的好处是相似的两段文本，Simhash 之后的值仍然能保持相似，而且经过了降维，储存空间也大大减少，计算效率会提高很多。一般来说，两端simhash的海明距离如果在3以内，就认为是相似文本。

你可能会问，为什么？为什么这种 Hash 方法可以让相似的文本仍然相似？Simhash的发明人 Charikar 的论文中并没有给出具体的证明，但由于 Simhash 是由随机超平面hash算法演变而来的，有人根据这个给出了证明，大家可以搜搜看。

二、加速查询：抽屉原理

虽然 Simhash 可以减少单次计算的耗时，海量文本来说，匹配的计算量还是很大的。如果数据库里有几百亿数据，那就意味着要匹配几百亿次。因此，我们需要一种方法来减少匹配。

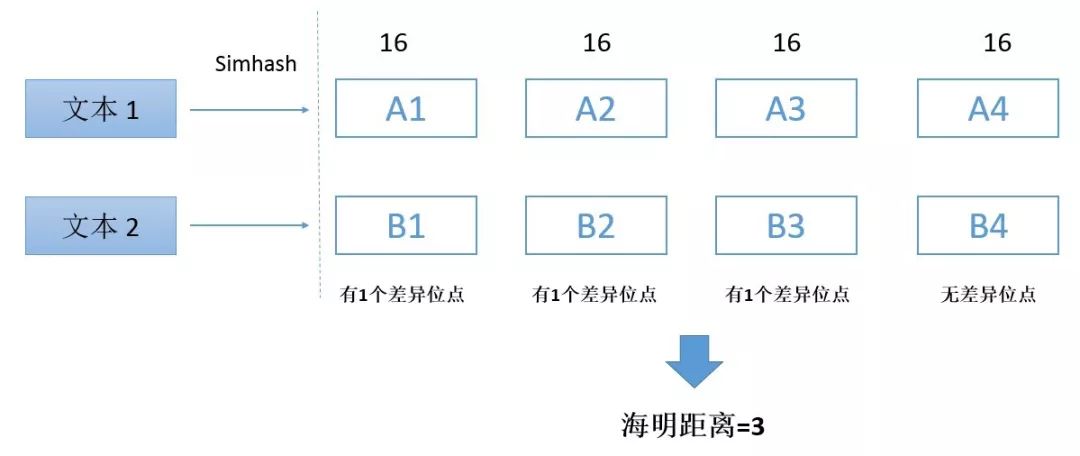
对于两段文本，我们分别映射成64位hash指纹之后，再每个文本分为四份，每个部分16位。对于这两段文本，如果海明距离在3以内，则它们对应的4个部分，至少有一个部分是一样的。

因为，海明距离小于3，意味着，最多有3个位点有区别，而3个差异位点分布在四个部分，至少有一个部分是没有相同的。

这就好比把3个球放到4个抽屉里面，一定有一个抽屉是空的，所以叫“抽屉原理”。

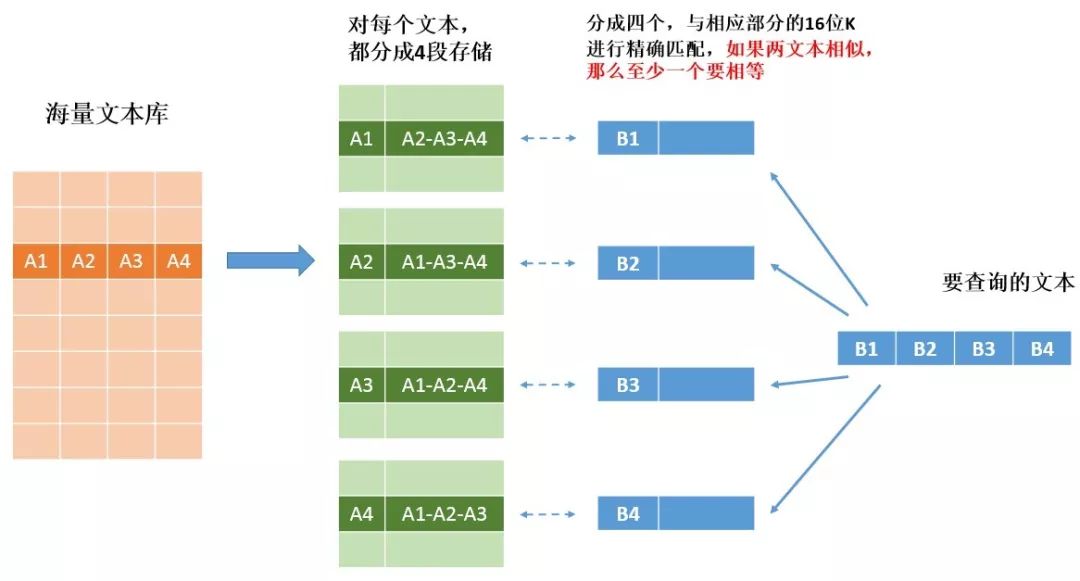
基于此，可以把一段64位指纹分成 K-V格式（Key-Value），K就是其中四个部分中的一个部分，V就是剩下3个部分。我们在匹配的时候，只要精确匹配K，K相同了，再去匹配V，这样可以大大减少计算量。

但问题是，我怎么知道差异位点分布在哪一部分？

所以，一段文本的Simhash指纹，我们需要复制成四次存储，以text1为例，simhash 成64位之后，我们分成四个部分，A1-A2-A3-A4。我们把这段存储四份，以使得每一部分都做一次K，剩下其他三个为V：

① K: A1, V: A2-A3-A4

② K: A2, V: A1-A3-A4

③ K: A3, V: A1-A2-A4

④ K: A4, V: A1-A2-A3

这样就可以保证不会有遗漏。

下图是查询的示例：

那么，用这一套方法，最终能减少多少查询呢？给大家算一笔账：

假设数据库中有 2^30 条数据，也就是差不多10亿条数据：

如果不用抽屉原理，那么就得与10亿条数据一一查询，即10亿次。
使用了抽屉原理，即与16位的K先查询。

想象一下由0/1组成的16位数字，可能有多少？最多2^16种K（每一位有0/1两种可能，一共有16位，排列组合一下）；
2^30数据，一共2^16种K，那么每个K-V返回的最大数量也就2^(30-16)=16384个候选结果，4个K的话，总的结果也就16384*4=65536，约66W。
这样一来，原来需要比较10亿次，现在只需要比较66万即可。

三、相关代码

后台回复【simhashcode】，提供simhash的Python代码

BAT招聘：

蚂蚁金服招人啦！| Hey bro, 这份工作太skr