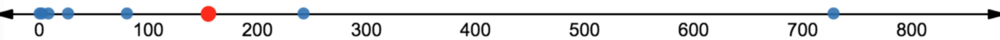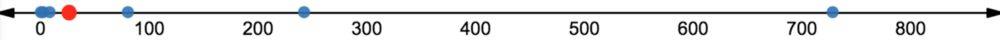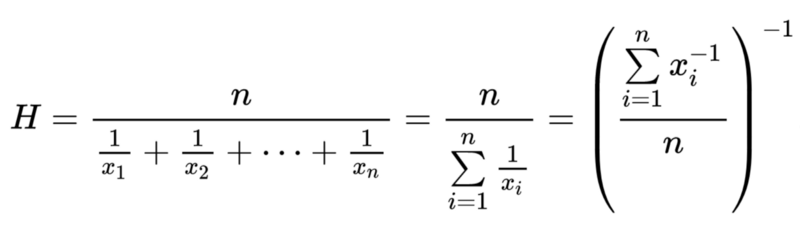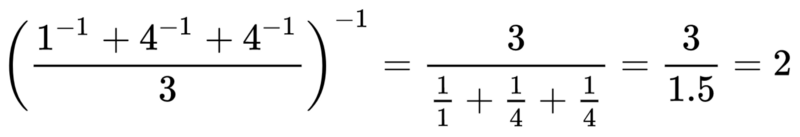平均而言，你用的是错误的平均数（上）：几何平均数和调和平均数

来源：Medium

编译：weakish

编者按：Philadelphia Media Network资深数据分析师Daniel McNichol介绍了不同平均数背后的直觉，以及如何、何时使用它们的经验。

前言

（如果你已经了解“集中趋势”，那么可以跳过这一节）。

不同平均数的比较；图片来源：维基百科

大概是最常见的数据分析任务

你有一组数字。你希望用更少的数字概括它们，最好是只用一个数字。因此，你将这组数字加起来，然后除以数字的数目。哇，你得到了“平均数”，没错吧？

也许。

和流行的观点不同，从数学上说，平均数通常不是一样东西。意思是：没有可以恰当地称作“平均数”的数学运算。我们通常所说的平均数是“算术平均数”，具体计算过程如前所述。我们称其为“平均数”，是因为我们期望它符合“平均数”的口头定义：一个典型的、正态的中间值。我们常常是对的，但正确的频率比我们想象的要低。

概述统计量

算术平均数仅仅是得到“平均”值的许多方法的其中之一。技术一点地说，这些属于概述统计量、集中趋势测度、位置测度。

中位数大概是第二出名的概述统计量。由于中位数是数据集中间的值，因此常常比均值更平均。我这里不讨论中位数，不过在许多情形下，算术平均数被滥用在中位数更合适的地方。更多关于中位数的内容，可以参考下面三篇文章：

• https://www.linkedin.com/pulse/20140715160509-29681087-median-vs-average-household-income/

• http://wkuappliedeconomics.org/indblogs/mean-vs-median-income-which-one-to-use-and-what-it-means-for-south-central-kentucky/

• https://medium.com/%40JLMC/understanding-three-simple-statistics-for-data-visualizations-2619dbb3677a

本文将重点讨论知名度相对较低的几何平均数和调和平均数。

毕达哥拉斯平均数

平方平均数和毕达哥拉斯平均数；图片来源：维基百科

算术平均数是3种毕达哥拉斯平均数之一（名称源自研究这些性质的毕达哥拉斯及其学派）。另外两种毕达哥拉斯平均数是几何平均数和调和平均数。

为了了解它们的基本功能，让我们从熟悉的算术平均数开始。

算术平均数

算术平均数的名字取得很合适：我们累加数据集中的所有数字，接着除以数据集包含的数字数目。

不过，加法没有什么特别的。它只不过是一种简单的数学运算。在数字之间存在可加性（additive）关系的数据集上，算术平均数效果很好。这样的关系经常被称为线性，因为如果我们将所有数字按升序或降序排列，数字倾向于落在一根直线上。一个简单而理想化的例子是公差为3的等差数列：

然而，不是所有的数据集都适宜用这种关系描述的。有些数据集内部存在乘法或指数关系，例如，公比为3的等比数列：

我们看到，算术平均数（156）并不特别接近我们的数据集中的大多数数字。实际上，它是中位数（27）的5倍。

将数据绘制在一根数轴上，能够更明显地看到这一扭曲。

所以，我们做什么？

引入……

几何平均数

由于数据集中数字之间的关系是相乘，我们通过乘法和取方根（总共有几个数字就开几次方根）来得到几何平均数。

我们可以看到，在等比数列上，几何平均数更能代表数据集的中间值。事实上，在这个等比数列数据集上，它等于中位数。

从单根数轴上也可以看到这一点：

几何平均数的真实世界应用

实际上，有很多实际场景适合使用几何平均数，因为类似相乘的关系在真实世界中很常见。

一个经典的例子是复利问题。

假设我们有一笔5年期存款，本金为$100,000，每年的利率是变动的：

年利率：1%、9%、6%、2%、15%

我们想要找到平均年利率，并据此计算5年后本金和利息的总和。我们尝试“平均”这些利率：

(.01 + .09 + .06 + .02 + .15) ÷ 5 = .066 = 6.6%

然后我们将平均利率代入复利计算公式：

100000 * (1.066 ** 5 - 1) + 100000 = 137653.11

比较以下不使用平均利率，直接计算的结果：

100000 * 1.01 * 1.09 * 1.06 * 1.02 * 1.15 = 136883.70

可以看到，我们的简便计算方法误差接近$1,000。

我们犯了一个常见的错误：我们将加法操作应用于相乘过程，得到了不精确的结果。

现在，让我们试试几何平均数：

1.01 * 1.09 * 1.06 * 1.02 * 1.15 = 1.368837042
1.368837042开5次方根 = 1.064805657

将几何平均数代入复利计算公式：

100000 * (1.0648 ** 5 - 1) + 100000 = 136883.70

这个数字正好等于我们逐年计算所得的结果。

我们使用了合适的平均数，并得到了正确的结果。

几何平均数还适合什么场景呢？

几何平均数的一个很酷的特性是，你可以对尺度完全不同的数字取平均数。

例如，假设我们想比较两间咖啡店来源不同的在线评价。问题在于，来源一的评价使用五星制，而来源二的评分评价使用百分制：

• 咖啡店A

• 来源一：4.5

• 来源二：68

• 咖啡店B

• 来源一：3

• 来源二：75

如果我们直接根据原始分值计算算术平均数：

咖啡店 A = (4.5 + 68) / 2  =  36.25
咖啡店 B = (3 + 75) / 2 = 39

根据上面的数据，我们得出结论咖啡店B是赢家。

如果我们对数字有一点敏感性，我们会知道在应用算术平均数得到精确的结果之前，我们首先需要标准化（normalize）数据集中的值至同一尺度。

所以，我们将来源一中的评价乘以20，将其从五星尺度拉伸到来源二的百分制尺度：

# 咖啡店A
4.6 * 20 = 90
(90 + 68) / 2 = 79
# 咖啡店B
3 * 20 = 60
(60 + 75) / 2 = 67.5

我们发现，其实咖啡店A才是赢家。

然而，几何平均数，允许我们在不考虑尺度问题的前提下得到一样的结论：

咖啡店A = (4.5 * 68) 的平方根 =  17.5
咖啡店B = (3 * 75) 的平方根 = 15

算术平均数被尺度较大的数字支配了，以至于得出了错误的结果。这是因为算术平均数期望数字间的加法关系，而没有考虑尺度和比例问题。所以需要在应用算术平均数之前将数字转换为同一尺度。

另一方面，几何平均数，很容易就能处理比例问题，因为它本质上是乘法关系。这是一个极为有用的性质，但注意我们损失了什么：我们不再具有可解释的尺度了。在这样的情况下，几何平均数其实是无单位的（unitless）。

例如，以上的几何平均数既不意味着百分制中的17.5分，也不意味着五星制中的15星。它们不过是无单位的数字，互相之间比例一致（技术上说，它们的尺度是原尺度5 & 100的几何平均数，也就是22.361）。不过，如果我们只需比较两间咖啡店评价的高低，那么这不会成为一个问题。

几何平均数回顾

• 几何平均数对值相乘，而不是相加，接着取n次方根，而不是除以n。

• 它基本上是在说：如果我们的数据集中的数字都是一样的，那么这个数字应该是什么，才能得到和实际数据集一样的乘积？

• 这使它非常适合描述相乘关系，例如比率，即使这些比率的尺度不同。（因此，它经常用来计算财经指数和其他指数。）

• 缺点： 应用几何平均数时，可能会丢失有意义的尺度和单位。另外，它对离散值的不敏感性可能会遮蔽可能具有较大影响的大数值。

和生活中的大多数事情一样，极少有牢不可破的规则说必须使用几何平均数（复利等少数情形除外）。有一些启发式的规则和经验规则，但无疑需要判断力和科学的怀疑，才能应用合理的经验。

在最后的总结中我们将继续讨论这些，不过现在让我们引入最后一种毕达哥拉斯平均数……

调和平均数

算术平均数需要加法，几何平均数则利用乘法，调和平均数使用倒数。

我们可以用语言描述调和平均数：数据集的倒数的算术平均数的倒数。

听起来当中包含很多倒数，但实际上不过是一些简单的步骤：

1. 对数据集中的所有数字取倒数

2. 找到这些倒数的算术平均数

3. 对上一步所得取倒数

源自维基百科的一个简单例子：1、4、4的调和平均数是2：

注意，由于0没有倒数，因此调和平均数和几何平均数一样，无法处理包含0的数据集。

好，我们已经明白数学部分如何工作了。不过调和平均数适用于哪些场景呢？

调和平均数的现实世界应用

为了回答上面的问题，我们需要回答：倒数适用于哪些场景？

由于倒数和除法类似，不过是伪装的乘法（乘法不过是伪装的加法），我们意识到：倒数帮助我们更方便地除以分数。

例如，5 ÷ 3/7等于多少？如果你还记得初等数学，你大概会将5乘以7/3（3/7的倒数）。

不过有一个等价的方法，将5和3/7缩放至共同的分母：

5/1 ÷ 3/7 = 35/7 ÷ 3/7 = 35 ÷ 3 = 11 2/3 = 11.66667

类似之前使用几何平均数作为快捷路径，在未标准化的情况下找到不同尺度评分的相加算术平均数的关系，调和平均数帮助我们在不操心共同分母的情况下找到乘/除关系。

因此，调和平均数很自然地成为几何平均数之上的另一层乘/除。因此，它有助于处理包含长度或周期不同的比率的数据集。

（你可能在想：“等一下，我原以为几何平均数用在平均利率和不同尺度的比率上！”你想的没错。你也不是第一个为此感到困惑的人。我自己写下下面的内容正是为了厘清我自己的思考和理解。我希望下面的例子让这个主题更清楚了，在文章后面的总结部分也会回顾所有的区别。）

平均速度

现实世界中，使用调和平均数的经典例子是以不同的速度通过物理空间。

考虑一次去便利店并返回的行程：

• 去程速度为30 mph

• 返程时交通有一些拥堵，所以速度为10 mph

• 去程和返程走的是同一路线，也就是说距离一样（5 miles）

整个行程的平均速度是多少？

同样，我们可以不假思索地直接应用30 mph和10 mph的算术平均数，然后自豪地宣布结果是20 mph。

但是再想一想：由于你在一个方向上的速度较高，因此你更快地完成了去程的5 miles，在那个速度上花了整个行程中更少的时间，所以整个行程期间你的平均速度不会是30 mph和10 mph的中点，它应该更接近10 mph，因为你更多的时间是以10 mph的速度行驶。

为了正确地应用算术平均数，我们需要判定以每种速率行驶所花的时间，然后以适当的权重加权算术平均数的计算：

1. 去程：5 / (30/60) = 10 minutes

2. 返程：5 / (10/60) = 30 minutes

3. 总行程：10 + 30 = 40 minutes

4. 加权算术平均数：(30 * 10/40) + (10 * 30/40) = 15 mph

所以，我们看到，真正的平均速度是15 mph，比使用未加权的算术平均数计算所得低了5 mph（或者25%）。

你大概猜到了我们下面要做什么……

让我们试着使用调和平均数：

2 / (1/30 + 1/10) = 15

真正的行程平均速度，自动根据在每个方向上使用的时间进行调整，是15 mph！

有一些地方需要注意：

• 可以直接应用调和平均数的前提是不同速度行驶的总距离是相等的。如果距离不同，我们需要使用加权调和平均数，或加权算术平均数。

• 当距离不等时，算术平均数仍然以不同速度行驶的时间作为加权，而调和平均数则以不同速度行驶的距离作为加权（因为通过取倒数，已经隐式地考虑了不同速度的时间比例）。

• 毕达哥拉斯平均数大部分的复杂性和麻烦源于比率的本质以及我们对比率的哪方面更感兴趣。例如，算术平均数总是用分母的单位表示。在行程问题中，比率是每小时的英里数，因此，算术平均数给出的结果是以分母（某种意义上隐藏的）单位表示，小时：(30m / 1hr + 10m / 1hr) ÷ 2 = 20m/1hr = 20 mph。如果我们在每个方向上所花的时间是一样的，那么这个结果会是精确的。然而，我们知道，在每个方向上所花的时间并不一样。相反，调和平均数通过取倒数翻转这些比率，将我们实际感兴趣的数字放入分母，接着取算术平均数，并再次翻转，给出我们要求的平均速度。（可以使用财经的P/E率更深入地探讨这一问题，请参阅论文Using the Price-to-Earnings Harmonic Mean to Improve Firm Valuation Estimates。）

• 几何平均数适用于复利问题的原因是，利率的周期是相等的：每种利率一年。如果周期是可变的，也就是说每种利率的持续时间不同，那么我们同样需要使用某种权重。

• 几何平均数可以处理相乘关系，例如复利问题和不同评分尺度上的比率，而调和平均数则通过神奇的倒数容纳了另一层次的乘/除关系，例如可变周期或长度。

类似复利问题和几何平均数，这是一个准确、客观正确的调和平均数的应用案例。不过，事情并不总是如此清晰。有其他准确的、可以在数学上论证的调和平均数的应用，包括物理、财经、水文学，甚至（源自传统）棒球统计。和数据科学关系更密切的：调和平均数经常用在评估机器学习模型的准确率和召回中。但是，在更多的情况下，调和平均数的应用需要判断力，需要你对数据和手头问题的灵活理解。

总结

1. 3种毕达哥拉斯平均数密切相关

例如，我们已经看到：

• 不同尺度评分的几何平均数有时保留了这些值标准化至同一尺度后的算术平均数的次序。

• 调和平均数等价于行程速度的加权算术平均数（权重为相对行程时间）

在下篇中，我们将看到，数据集的几何平均数等价于数据集中每个数字的对数的算术平均数。所以，正如调和平均数不过是算术平均数加上一些倒数变换，几何平均数不过是算术平均数加上对数变换。

2. 毕达哥拉斯平均数遵循严格的次序

根据相应的公式，调和平均数总是小于几何平均数，几何平均数总是小于算术平均数。

这三种平均数是彼此接近还是互相远离，取决于数据的分布。以上规则唯一的例外是，在数据集中所有数字相等的极端情形下，3种平均数同样相等。也就是说，以下不等关系成立：

调和平均数 ≤ 几何平均数 ≤ 算术平均数

从本节开头的毕达哥拉斯平均数的几何描述中也能看到这一点。

认识到这一次序关系有助于理解何时应用哪种平均数，以及不同平均数对结果的影响。

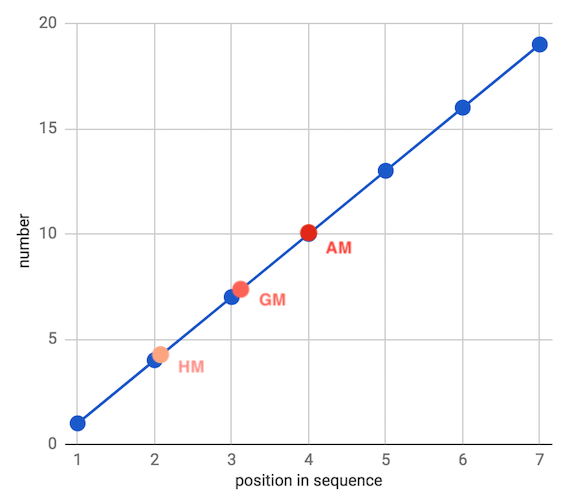
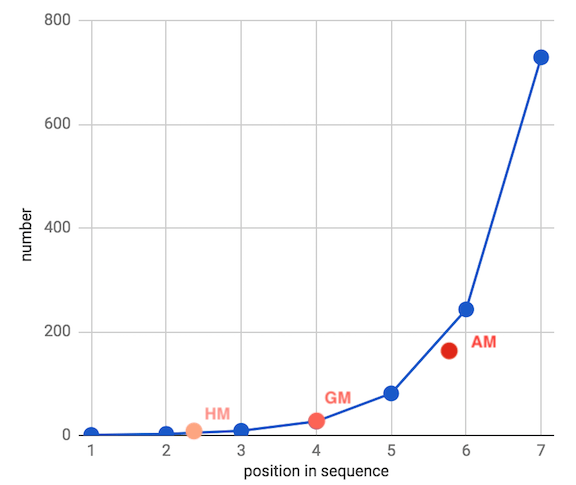
让我们回顾之前的相加和相乘数据集，这次我们将画出所有三种平均数：

很明显，几何平均数和调和平均数看起来要比这一线性、相加数据集的中间低不少。这是因为这两种平均数对较小的数字而不是较大的数字更敏感（让它们相对而言对较大的离散值不敏感）。

这里，几何平均数准确地位于数据集的中点，而调和平均数则向低端扭曲，算术平均数则受较大的离散值的影响，向高端扭曲。

描绘一个集中趋势用调和平均数表达最佳的数据集并不容易，因此我将直接转入下一部分……

3. 强硬的规则，一些启发式的方法，和许多判断的空间

• 不同尺度的比率：使用几何平均数（或在标准化的数据上应用算术平均数）。

• 周期一致的复合比率：使用几何平均数。

• 不同周期或长度上的比率：使用调和平均数（或加权平均数）。

• 了解比率的哪一边你更感兴趣，以决定应用哪种平均数。算术平均数是以分母的单位表达的（显式或隐式）。调和平均数让你可以倒置比率，让结果以原本分子的单位表达。

• 如果数据体现出相加结构：算术平均数通常是安全的选择。

• 如果数据体现出相乘结构和/或包含较大的离散值：几何平均数或调和平均数可能更合适（中位数可能也比较合适）。

• 任何决定都有缺陷和折衷：

• 使用几何平均数可能损失有意义的尺度或单位。

• 包含0的数据集无法应用几何平均数或调和平均数，包含负数的数据集意味着无法应用几何平均数。

• 使用几何平均数或调和平均数时，受众可能不熟悉这两个概念。

• 经常，更实用、更易解释的方法是：

• 存在较大的离散值时直接使用中位数

• 移除离散值

• 使用加权算术平均数或统计学变换，而不是难懂的毕达哥拉斯平均数

• 统计计算语言R内置矩阵求逆和三次样条插值的方法，却没有内置计算简单的几何平均数或调和平均数的函数，这可能多少暗示了这两种平均数狭窄的使用场景。（不过Google sheets和Excel倒是包含这两种平均数。）

如果要用一句话概括整篇文章，那么：

理解数据的本质，仔细思考你用来描述数据的概述统计量，才能避免用错平均数的风险。

请留言分享你使用这两种不那么常见的毕达哥拉斯平均数的案例和经历（以及你发现的本文的错误）。

本文的下篇将从更技术的角度，通过真实、合成数据，分布，绘图，R代码，进一步讨论这一主题，敬请期待。

我的Twitter、LinkedIn、Github的用户名均为dnlmc，欢迎关注。

原文地址：https://towardsdatascience.com/on-average-youre-using-the-wrong-average-geometric-harmonic-means-in-data-analysis-2a703e21ea0