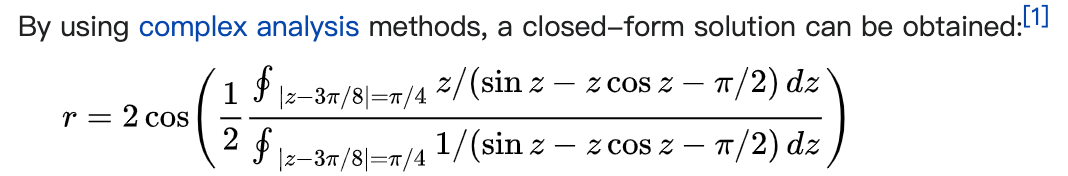诞生272年后，这个看似简单的数学问题终求得闭式解

会员服务 ·

诞生272年后，这个看似简单的数学问题终求得闭式解

2020 年 12 月 13 日 机器之心

机器之心报道

参与：魔王

德国数学家 Ingo Ullisch 破解诞生 270 多年的「山羊问题」，求出闭式解。

我们先来看一个「简单」的问题： 假如圆形篱笆围出一英亩草地，将一只山羊拴在篱笆内，你需要用多长的绳子才能让羊吃到半英亩的草 ？

这看起来像高中几何题，但事实上 270 多年来，许多数学家和数学爱好者都在思考这个问题及其不同形式。他们成功解决了一些版本，但也只是模糊的不完备的答案。

数学家 Mark Meyerson 曾表示：「没人知道这个基础原始问题的确切答案，目前给出的都是近似解。」

但在今年初，德国数学家 Ingo Ullisch 最终破解了这一问题，得出了首个精确解。数学家 Michael Harrison 表示：「我认为这是首个绳长的显示表达式，这当然是进步。」

Ingo Ullisch 使用复分析求出了山羊问题的精确解。

Ullisch 表示，这并未颠覆教科书或改革数学研究，因为这只是个孤立的问题。但即使这样的有趣问题也可能带来新的数学想法，帮助研究人员提出解决其他问题的新方法。

有趣的「山羊问题」

这个问题的第一个版本出现在 1748 年的伦敦期刊《The Ladies Diary: Or, The Woman’s Almanack》上。

当时的问题情境是「拴马」：将马拴在圆形篱笆外面，如果绳长和篱笆周长相等，那么马能吃到的最大面积是多少？这个问题版本后来被分类为「外部问题」，因为该问题中马在「圆形篱笆外面」。

该期刊次年刊登了一份来自「Mr. Heath」的答案。Heath 通过「试验和对数表」得出了结论——100 码的绳子，76,257.86 平方码的面积（绳长约 91.44 米，面积约 63,761.28 平方米）。

但这是近似解而非精确解。我们可以通过一个例子来了解二者的区别：设公式 x^2 − 2 = 0，可以得出近似数值解 x = 1.4142，但这并不准确，无法等同于精确解 x = √2。

1894 年，这个问题在《美国数学月刊》第一期中再次出现，并被改写为最初的「 篱笆内吃草问题 」。这被分类为「内部问题」。Ullisch 认为内部问题比外部问题难度更大。外部问题是已知圆半径和绳长，求吃草面积，这可以通过积分来解决；而内部问题则相反，给出面积求绳长，要复杂得多。

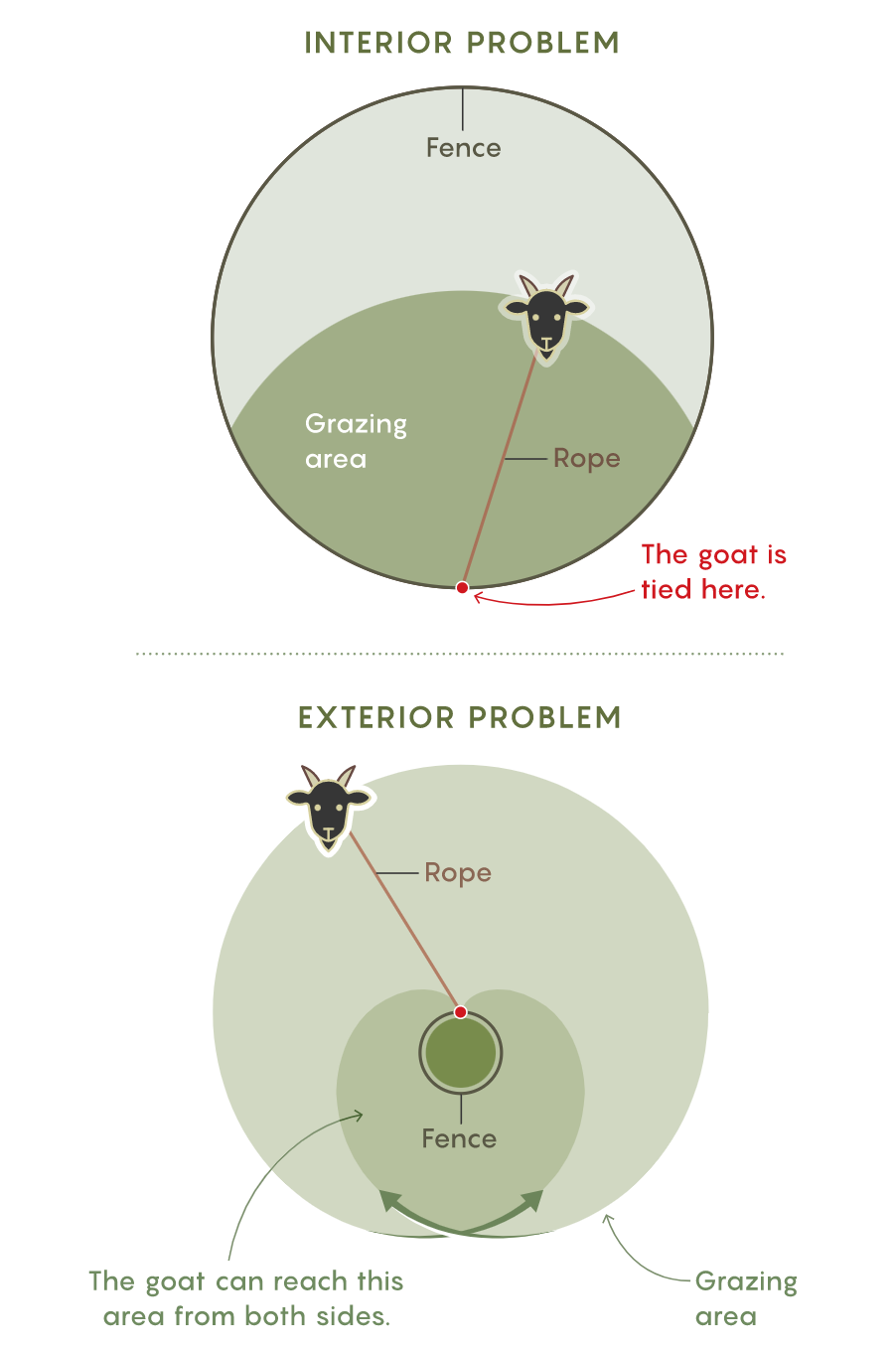
山羊吃草问题有两种形式。内部问题是给出吃草面积求绳长，外部问题是给出绳长和篱笆周长求吃草面积（绳长等于篱笆周长）。

接下来的几十年里，《美国数学月刊》刊登了该内部问题的多个变体，主角大部分是马偶尔是骡子，篱笆有时是圆的，有时是方的，还有椭圆的。到了 1960 年代，山羊逐渐取代了马的位置，成为该问题的主角。

1984 年，数学家 Marshall Fraser 创造性地将这一问题从草地扩展到了更广阔的区域。他求出了允许山羊在 n 维球面一半体积中吃草所需的绳长（n 趋向于无穷大）。Meyerson 发现了其中的逻辑错误并纠正，得到了相同的结论： 随着 n 趋向于无穷大，绳长和半径的比接近√2 。

Meyerson 表示，这种表示该问题的方式看似更复杂了（多维空间而不是草地），但实际上却让求解的过程更简单了。「在无穷维中，我们有清晰的答案，而在二维中并没有这样明确的解。」

1998 年，美国海军学院教授、数学家 Michael Hoffman 将外部问题扩展到了不同的方向。他看到的外部问题是「将牛拴在圆形牛栏外面，牛可以吃到多少面积的草？」，Hoffman 将原本问题中的圆形扩展到平滑的凸曲线，包括椭圆甚至非封闭曲线。

Hoffman 假定该问题中绳长（长度为 L）小于或等于曲线的周长。他首先绘制曲线上拴牛点的切线，牛可以在切线范围内 πL^2/2 的半圆区域内吃草；然后针对切线和曲线间的空间求得精确积分解，从而确定吃草面积。

最近，英国兰卡斯特大学数学家 Graham Jameson 和其子 Nicholas 求出了内部问题三维版本的解。Graham 表示：「三维问题比二维问题简单一些。」

利用复分析，求出「山羊问题」闭式解

然而，1894 年出现的二维内部问题仍未出现精确解，直到 Ingo Ullisch 今年初在期刊 Mathematical Intelligencer 上发表了一篇论文。

论文地址：https://link.springer.com/article/10.1007/s00283-020-09966-0?shared-article-renderer

Ullisch 第一次听到山羊问题是在 2001 年，当时他还是个孩子。2017 年，在获得了德国明斯特大学博士学位后，他开始研究这个问题。他想尝试一种新方法。

当时大家都知道，山羊问题可以被简化为一个超越方程（transcendental equation），包含正弦、余弦等三角函数项。和很多棘手的超越方程一样，这会带来障碍，例如 x = cos(x) 没有精确解。

Ullisch 将这个问题设置为较易处理的超越方程：sin(β) – β cos(β) − π/2 = 0。尽管这个方程看起来也挺难，但他认为可以使用 复分析 来解决。复分析是对包含复数的表达式使用分析工具的数学分支，已经诞生好几个世纪，但 Ullisch 是第一个使用复分析解决山羊问题的人。

通过这一策略，Ullisch 将超越方程转换为「绳长允许山羊在圈场一半面积内吃草」的等效表达式。也就是说，他最终用准确的数学形式回答了这一问题。

但这个回答存在一个问题，就是其复杂度不像 √2 那么简单，它更加深奥。