Image to Image Translation Using GAN | 每周话题精选 #04

➊
何谓配对数据?
A: 给定一张图,该图在另外一个域中的转换目标已经确定的话,就称该图与该图的转换目标为配对的,这种数据就称为配对数据。
比如你想要把一个正常的男性人脸“娘化”,这样一个任务,如果有大量的、成对的正常男脸与对应的娘化人脸,那它就是一个简单的有监督问题。反之,如果你只有一堆男脸和一堆娘化脸,但是不知道它们之间有什么对应关系,那就是无配对的情况。
配对一般是为了使输入和输出共享一些共同的特征,目标明确,训练起来相对简单。在不配对的数据集中没有这种有意义的变换,训练也相对复杂。目前来说,配对数据非常匮乏,所以今天主要讨论无配对数据的跨域图像转换问题。
➋
没有配对数据的跨域图像转换,有哪些 GAN 的方法?
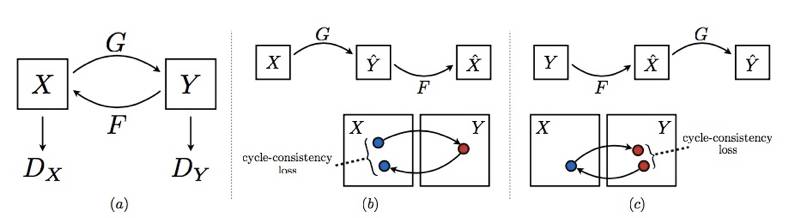
A: 针对图像转换问题,Cyclegan,Dualgan,Discogan 三兄弟提供了很好的思路,模型大致框架如下图所示,具体的介绍可参见:
https://zhuanlan.zhihu.com/p/26332365
在上面的框架图中,G 和 F 是生成器,Dx 和 Dy 是判别器。G 和 F 可以分别看成 Autoencoder 中的 Encoder 和 Decoder,Encoder 将 X 所在的域中的图像翻译成 Y 所在域中的图像,Decoder 反之。而 Loss 除了传统 GAN 的散度 loss 之外,还应该加入重构误差。
无配对图像转换(以 X 转换到 Y 为例)有两个要求,一是X转换得到的图像 Y 要符合 Y 所在的域中图像的总体风格(小尺度特征);二是 Y 要尽量保持 X 中的总体内容(大尺度特征)。前者通过降低散度 loss 来实现,后者通过降低重构误差来实现。
➌
关于中间层重构
A: 上部分所说的重构误差是针对最终得到的图像的,而中间层重构会针对图像更抽象的特征进行考量,ImprovedGAN 中的 feature matching 和 MMD(maximum mean discrepancy)都可以看做中间层重构。
MMD 的核心思想是让真实分布和生成分布的一些统计量相同。有很强的理论保证,两个分布的某些统计量的相似性正比于分布的相似性。
具体到 MMD,如果两个分布 p1 和 p2 完全相同,那它们经过随便任何变换 f 之后的均值也会完全相同。所以反过来我们搞一堆各种各样的 f,让 p1 和 p2 在这些 f 变换后均值拉近,这样就简介拉近了原始的 p1 和 p2。
➍
关于 DTN
A: 对于无配对数据的转换问题,DTN(Domain Transfer Network)提供了另外一种方案。
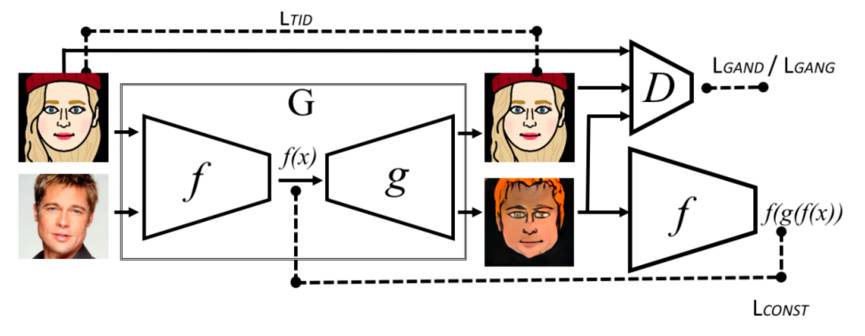
DTN 的主要框架如上图所示,其主要思想是 X 域的图像经过关于 Y 域图像的自编码网络后,也会染上 Y 域图像才有的一些特征。
如上图所示,G 可以看作关于动漫图像的 AutoEncoder。G 需要满足的条件是,动漫头像经过 G 之后,基本保持不变。而真实图像经过 G 之后会被动漫化。
D 网络会判别真实图像是否真正被动漫化。经过动漫化的真实图像再次经过 G 的 encoder 所得到的编码,与真实图像本身经过 G 得到的编码要是一样的。模型的 loss 由三部分构成:一是动漫域图像自编码网络本身的重构误差,二是真实图像动漫化之后的可区分度,三是编码器对真实图像动漫化所需特征的保持。
❺
解决没有配对数据问题的关键在哪里?
A: 一是判别网络 D 要能准确判别图像的真伪,以保证图像能从一个域转换到另一个域;二是需要一个 identity preserving loss 去引导生成网络 G 以保持图像的 identity 和自身结构。
❻
关于 loss 设计
A: 对抗 loss 要求输出图片在小尺度信息上像目标图片集合中的真实图片,重构 loss 要求输出图片尽量保留原图的大尺度信息,包括 identity 和 structure 等。
重构 loss 有 L1、L2,前者容易学到锐利清晰的图像,后者容易学到模糊的图片。
一般 GAN 的 loss 比较“贪婪”,想要“比真实样本还真”;MMD的loss比较“保守”,仅仅要求“和真实样本一样”;最小二乘的 loss 更加“保守”,仅仅要求走到介于真实样本和生成样本的中间地带(判别器二分类决策面附近)。
MMD 思想的比喻:G 为了打败 D,需要“揣摩”D 的“心思”,然后生成更符合 D 的“心思”的图像。
具有 MMD 思想的一些东西:neural style 中由的 gram matrix 计算出来的 perceptual loss (本质是二阶多项式核的 MMD),improved GAN 的 feature matching,wasserstein GAN(最后的输出某种意义上可以看做 mmd 变换的均值, 只不过这个变换是学出来的不透明的)。
文末福利
想要获取干货满满的完整版聊天实录?
请在 PaperWeekly 微信公众号后台回复“20170628”获取下载链接。
参与讨论
请长按识别以下二维码添加群主微信,备注「GAN」申请入群。
关于PaperWeekly
PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域,欢迎在公众号后台点击「交流群」,小助手将把你带入 PaperWeekly 的交流群里。