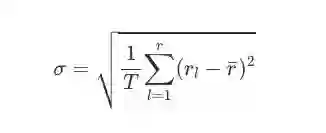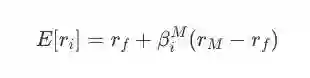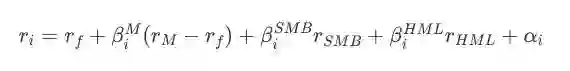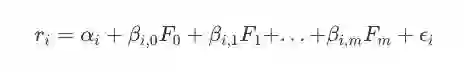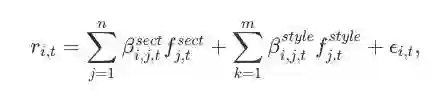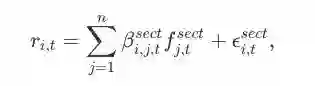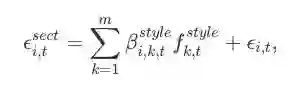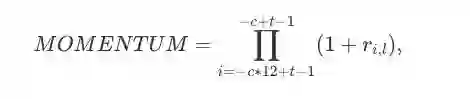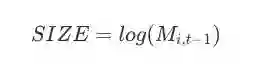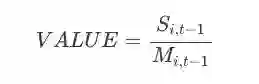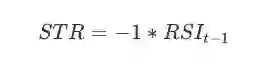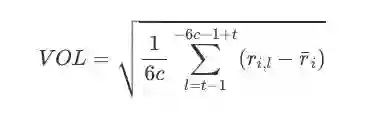Quantopian发布risk model白皮书，宛如一棵假韭菜

来源： Quantopian

编译：Bot

编者按：Quantopian是一个美股量化策略平台，开发者可以在上面利用官方免费提供的历史美股价格、公司基本数据和其他数据编写自己的Python模型并进行回测，或用模型参加官方主办的竞赛。“和华尔街同场竞技！”这是Quantopian在网页封面上打出的标语。而就在昨日，Quantopian也首次在网站上披露了自家独立开发的risk model的白皮书，虽然内容直白易懂，但它却有些令人大跌眼镜……

摘要

risk modeling（风险建模）是一个强大的工具，它有助于了解和管理投资组合中的风险来源。在这份白皮书中，我们介绍了Quantopian自主开发的Quantopian Risk Model (QRM)的逻辑和实现，这是一个能分解、归类各种股权投资策略风险敞口的股权风险因子模型。通过定义风险来源，它可以把剩余时间或由技能带来的投资回报部分作为策略的超额收益（alpha）。

简介

所谓风险管理就是我们为了未来将要获得的收益愿意承担多少风险，它涉及：

1. 识别风险来源；

2. 量化这些风险来源的敞口；

3. 确定这些风险敞口的影响；

4. 制定协调策略；

5. 观察后续表现，并根据需要修改协调策略。

投资中的风险来自未来投资组合收益和损失的不确定性，对于不同人和不同机构来说，他们对风险的容忍度各有不同。在这里，我们把T时间段内的总风险量作为该投资组合收益的风险量标准差：

其中，

• r_l 是l时的风险；

• r拔 是T时间段内该投资组合的总风险。

这是关于风险的一个常见定义。它能对称地处理收益和损失，适用于从个人资产到投资组合等不同级别投资的评估。标准差也称波动率，它提供了一个能衡量当前值和均值的接近程度的尺度。其中一个常见法则是68–95–99.7（标准正态分布），即有68%的数据位于距均值小于一个标准差之内的数值范围内，有95%的数据位于距平均值小于两个标准差之内的数值范围内，有99%的数据位于距平均值小于三个标准差之内的数值范围内。标准差越低，接近均值的个体就越多；标准差越高，观察个体中包含的极值就越多（无论是收益还是损失）。这符合我们对投资回报的一般见解：投资组合风险越高，相应的收益也可能越高，破产的几率也越大。

评估风险不仅仅是为了评估潜在的损失风险，它同样也能帮我们更合理地设定投资预期，并对潜在投资做出明确决策。量化风险来源的敞口的作用是揭示投资组合究竟达成了多少预期目标。例如，如果我们的投资策略面向市场和行业，那在基础投资组合中，我们就不应该长期投资技术领域资产或依靠技术资产获得大部分收益。虽然这种策略只在特定时期内有回报，但比起盲目下注赌博，这样的收益是有根据的，投资者能基于行业现状合理决定是否应该分配资金/该分配多少资金。

构建风险模型（risk model）能帮我们明确区分风险的普通风险（common risk）和特殊风险（specific risk）。这里的普通风险指的是推动股市收益变化的一些普通因素，它包括市场基础投资资产的基本信息和统计信息。其中市场的基本信息是股票发行公司的公示信息，如市净率和每股收益。这些数据不难收集。而统计信息则是用数学模型得出的资产收益和时间序列之间的相关性，它无需考虑公司的特定基础数据（Axioma，Inc. 2011）。

一些普通风险是整个股市波动带来的副产品。如资本资产定价模型CAPM（Sharpe 1964）的一个想法是一些风险是投资于个别行业而产生的风险，而BARRA模型（BARRA，Inc.，1998）、Fama-French三因子模型等金融风险控制模型也会模仿投资风格等因素，如投资小盘股或“高增长”公司。

特征风险指的是模型中普通风险难以解释的那些风险。通常情况下，这是模型设计者在考虑完所有普通风险后剩下的部分（Axioma，Inc. 2011）。当我们在定量交易背景下考虑风险管理时，我们对风险的理解在很大程度上依赖于摘要中提及的对alpha收益的定义。考虑完投资组合的普通风险后，这个残差可以被认为是模型的alpha收益。

因子模型

CAPM是第一个针对风险因子建模并阐述了普通风险概念的模型。在CAPM中，我们只用一个普通风险——市场本身的回报就能定义收益与普通风险因子之间的均衡关系。

上述等式表示单个投资i的回报，其中，

• r_f 表示无风险资产回报率；

• r_M 表示市场期望回报率；

• β_i^M = CON[r_i,r_m] / VAR[r_M] 表示第i个投资在市场上获得的超额收益（是个敏感性系数）。

CAPM把投资组合的收益分解为市场收益和无风险资产预期收益两部分。这是个不存在于现实世界的朴素观点。事实上它从提出以来也经历了多次改进，如Fama-French三因子模型。后者把两个风险源扩展为三个风险源——市场、公司规模和公司价值。以下是它的表达式：

其中，

• r_SMB 是市值因子（SMB）的风险溢价回报率；

• r_HML 是账面市值比因子（HML）的风险溢价回报率；

• β_i^SMB 是r_i相对于SMB的风险敞口；

• β_i^HML 是r_i相对于HML的风险敞口；

• α_i 是输入i后得到的误差项。

1976，Ross提出了一个新型模型APT，它结合了CAPM及其他类似模型，做到了在保证收益驱动时兼顾平衡多个因子影响。APT用多元线性回归表示单个资产的回报，它的表达式如下所示：

其中，

• F_j, j∈{0,m} 表示K种因素组成的列向量；

• β_i,j, j∈{0,m} 表示r_i 表示相对于各种因子的风险敞口；

• α_i 是常数组成列向量；

• ϵ_i 是随机误差列组成的列向量。

可以发现，APT中的因子完全由单一特征支配。在Fama-French模型中，我们解释收益的因子仅限于市场、SMB和HML；而在APT中，模型允许添加更多的因子，因此我们可以添加更多常见变量用来解释收益的变化情况。Quantopian风险模型的基础正是APT。

实现

QRM是一个多因子风险模型，它旨在用16个风险因子（包括11个sector因子和5个style因子）分解每项资产的回报率，但没有明确建立独立的市场因子模型。这些普通风险因子彼此独立，旨在尽可能全面地解释市场投资回报。

需要注意的一点是，QRM的设计目标是模拟历史和当前风险，它不能作为风险预测工具。

符号指南

• 小写字母表示向量，如a；

• 大写字母表示矩阵，如A；

• 下标中的后一个字母，如A_i,j，表示矩阵A中的第j列；

• 下标中的前一个字母，如A_i,j，表示矩阵A中的第i行。

数学模型

在数学上，QRM的表达式如下所示：

其中，

• r_i,t 表示资产i在t日的收益；

• n 表示sector因子的数量；

• m 表示style因子的数量

• β_i,j,t^sect 表示t日，第j个sector因子对资产i产生的风险。factor exposure（也称factor loading）指的是因变量和潜在变量之间的关系，如对于资产i，如果第j个sector因子和它没关系，则β_i,j,t^sect=0；

• f_j,t^sect 表示t日，第j个sector因子的返回值；

• β_i,k,t^style 表示t日，第k个style因子对资产i产生的风险。

• f_k,t^style 表示t日，第k个style因子的返回值；

• ϵ_i,t 表示资产i在t日的误差项（用model (1)计算）。

model (1) 的数学形式包括子模型1a和1b两部分。1a是：

1b是：

其中，ϵ_i,t^sect是1a模型中资产i在t日的误差项。

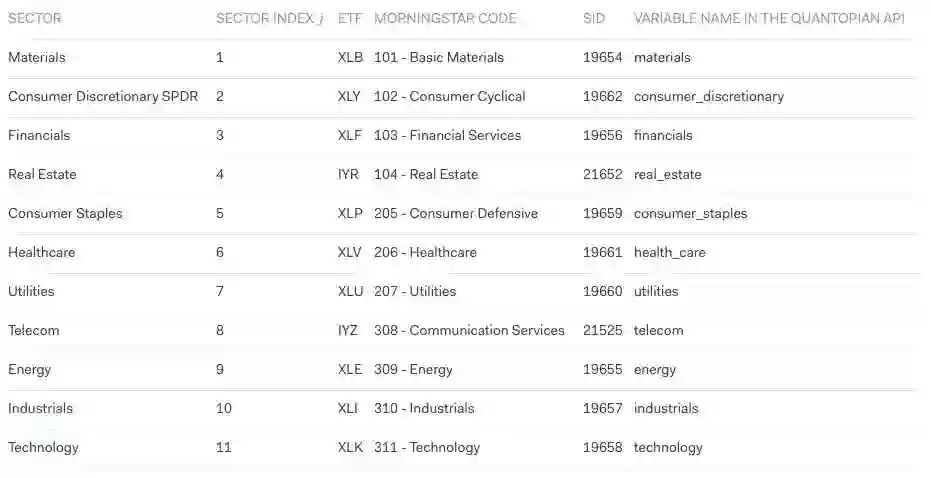
Sector因子

所谓Sector因子指的是不同行业对资产收益造成的风险。QRM沿用了晨星（Morningstar，Inc.nd）的行业分类方式，并引入ETF的行业回报作为sector因子的回报。下表是经model (1) 处理后各类因子的情况：

每个行业的回报都是已知的，Quantopian数据库中的每项资产都至多映射到某一个单一行业，所以现在我们只需估计相应的factor exposure。

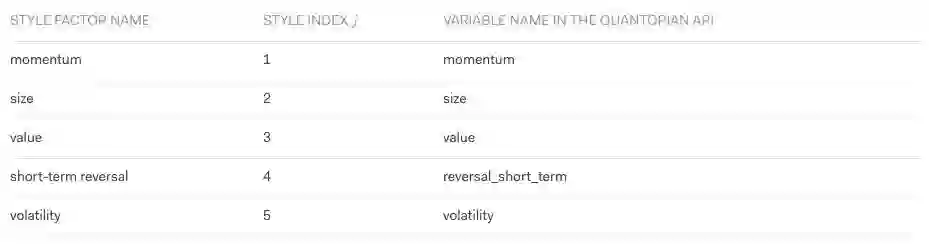
Style因子

QRM包括5种Style因子：动量、规模、价值、短期反转和波动性。每个Style因子都旨在复制传统的投资策略。下表是经model (1) 处理后各类因子的情况：

动量（momentum）：动量因子反映了过去的11个月内上涨股票（盈利）和下跌股票（亏损）之间的回报差异。

其中，

• r_i,l 表示资产i在l日的投资回报；

• c 表示一个月内的交易日数，这里它是一个常数21。

规模（size）：规模因子反映了大盘股和小盘股之间的回报差异。

其中，M_i,t-1 是资产i在t-1天的市场总值，Quantopian的公司数据是通过API从晨星基本数据中获取的。

价值（value）：价值因子反映了低价股和高价股之间的回报差异。

其中，S_i,ti-1 指的是资产i在公司中可获得的股东分红。

短期反转（short-term reversal）：短期逆转因子反映了亏转盈反弹和赢转亏暴跌股票治安的回报差异。

其中，RSI 是从t-1到t-15这14天内的股票相对强度指数。

波动性（volatility）：波动性因子反映了高波动性股票和低波动性股票之间的回报差异。

其中，

• c 表示一个月内的交易日数，这里它是一个常数21。

• r_i拔 是资产i在 (-6c−1+t,t−1)这个时间段内的平均收益率。

小结

除了以上内容，白皮书还介绍了sector因子和style因子的具体计算方式，考虑到篇幅因素，小编到此打住，感兴趣的读者可以前往原文地址查看。此外，白皮书中也没有给出模型的具体效果，所以就文章内容来看，这还是基于经典风险模型的一个尝试，而且技术非常简单，甚至有些过于“水”了。

所以如果是想做量化的新手，而且有拿到数据的路子，你可以照着这个架构去学习、复现。对于专业做量化的读者，如果说这就是Quantopian的真实水平，你们想说什么就在评论里尽情说吧。

原文地址：www.quantopian.com/papers/risk