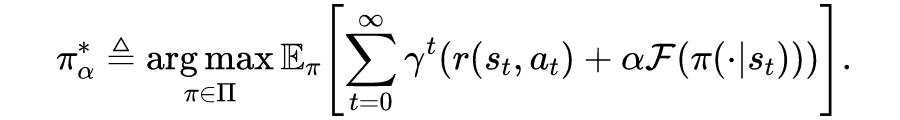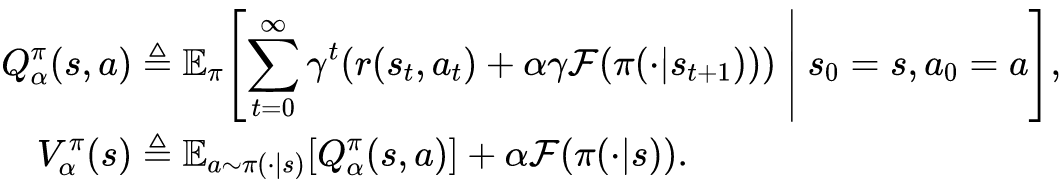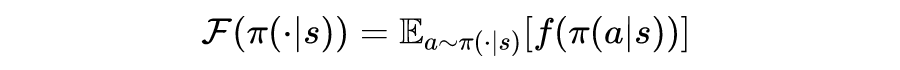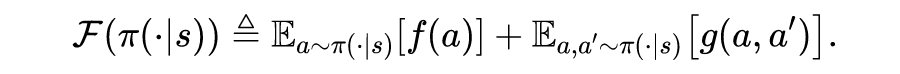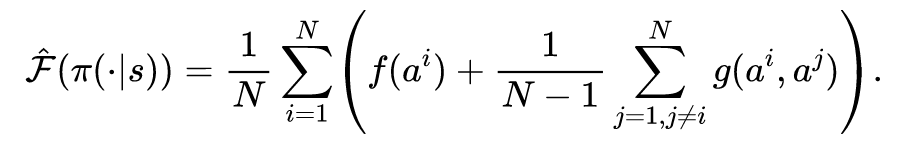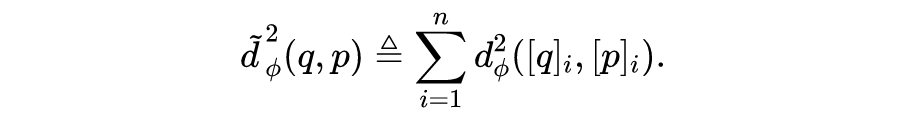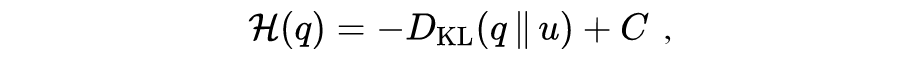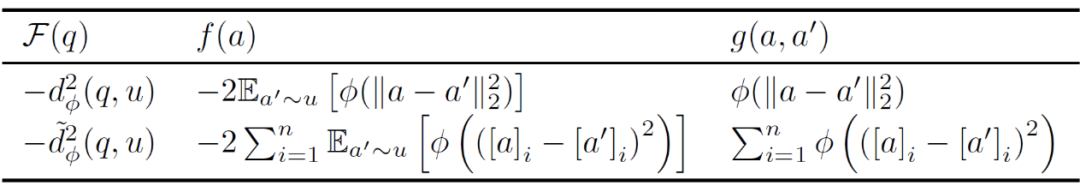NeurIPS 2020 | 一种基于动作采样的简单高效的正则化强化学习方法

论文标题:
Promoting Stochasticity for Expressive Policies via a Simple and Efficient Regularization Method
论文链接:
https://proceedings.neurips.cc//paper/2020/file/9cafd121ba982e6de30ffdf5ada9ce2e-Paper.pdf
代码链接:
https://github.com/MIRALab-USTC/RL-ACED
引言
相较于 model-based 类方法,model-free 类方法的实现和分析往往都相对简单。在 model-free 强化学习方法中,我们需要最大化累积回报的期望,因此最后习得的策略往往接近于一个确定性策略。然而,相比于确定性策略,随机策略更有利于探索未知环境,且在环境参数发生变化时具有更好的鲁棒性 [2,3],因此我们更希望训练得到的策略是随机策略。
为了促进策略的随机性,过往工作使用了熵正则化方法。该类方法在最大化累积奖励的同时,最大化动作分布的熵。如,soft Q-learning [4] 和 SAC [3,5] 使用 Shannon 熵作为正则项;sparse PCL [6] 和 TAC [7] 使用 Tsallis 熵作为正则项。
然而,在考虑连续的工作空间时,熵正则化的强化学习方法会陷入「表达能力有限的简单策略」与「复杂低效的训练过程」之间的两难选择。例如,SAC 往往使用简单的高斯分布表示策略,而 soft Q-learning 需要复杂低效的采样和推理过程来优化策略。
背景介绍
熵正则方法的局限性
-
熵正则的估计需要计算所选动作的概率密度(probability density),而使用复杂策略时其计算往往低效繁琐。 例如,使用标准化流(normalizing flow)表征策略时 [9] ,需要额外的串行过程计算概率密度;通过集成多个概率分布来表示策略时,需要计算每个分布的概率密度再进行平均。 -
熵正则的定义往往需要动作分布具有连续的累积分布函数,而使用复杂策略时该函数可能并不连续。 例如,使用基于狄拉克混合分布(Dirac mixture)表征策略 [10] 时,其动作的累积分布函数是阶梯状的不连续函数;使用噪声网络(noisy network)表征策略时,由于 Relu 激活函数的影响,动作分布的累积分布函数也可能出现不连续的情况。

4.2 基于广义能量距离的实例
4.2.1 广义能量距离
上节中我们给出了基于样本的正则项的表达式,在本节中,我们将基于广义能量距离给出上述正则项的一系列具体实例。
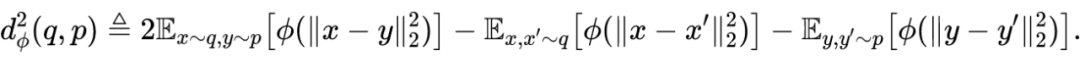
4.2.2 两个实例
▲ 表2:基于广义能量距离导出的 SBR 实例
基于能量距离的 actor-critic 算法
实验结果
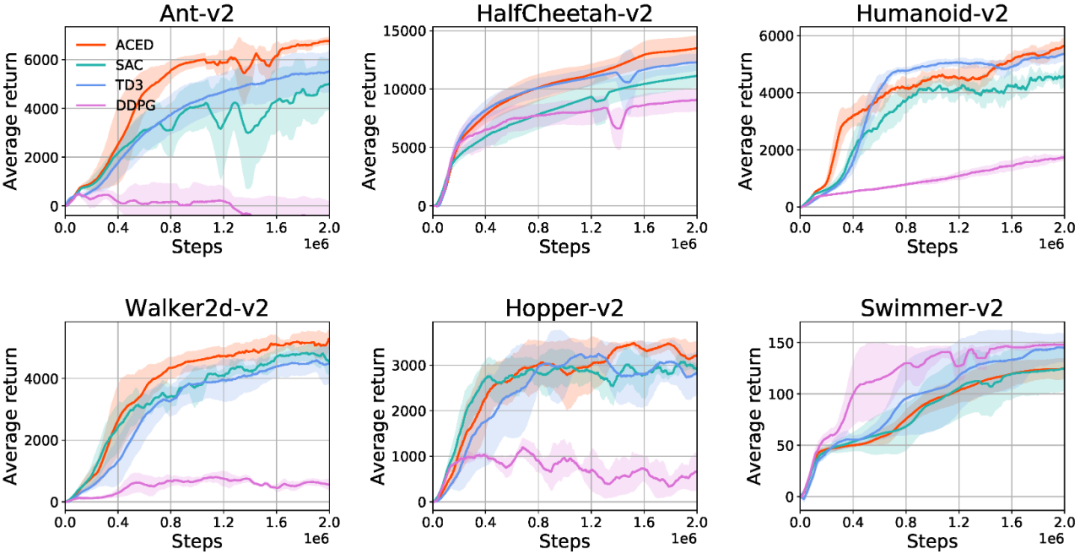
▲ 图1:6个不同任务下ACED算法与SAC、TD3、DDPG等算法的性能比较

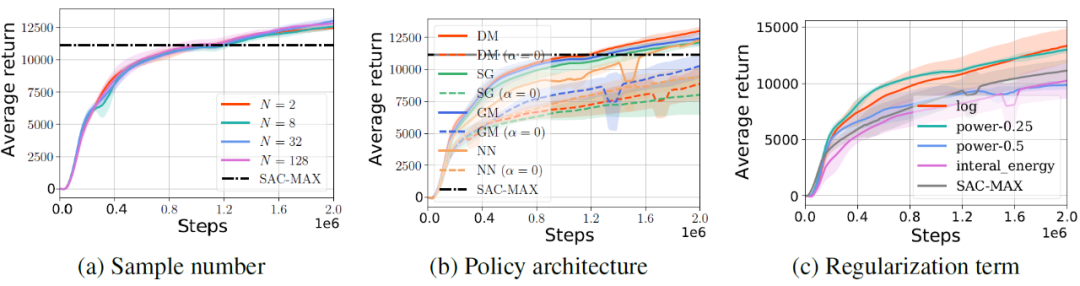
6.3 对比和消融实验
总结
在本文中,我们提出了一种基于动作采样的正则项 SBR,并基于广义能量距离(GED)给出了该正则项的一系列实例。SBR 作为熵正则的一种替代方案,能够广泛兼容各种复杂的策略结构,并具备计算高效、样本效率高等诸多优势。然而,“是否还能找到其他更好的 SBR 实例?”,“广义能量距离能否应用于强化学习的其他任务?”,这些问题仍待进一步解决和完善,我们也欢迎大家进行相关研究和讨论。
关于作者
周祺,2019年毕业于中国科学技术大学计算机科学与技术学院,获得工学学士学位。现于中国科学技术大学电子工程与信息科学系的 MIRA Lab 实验室攻读研究生,师从王杰教授。研究兴趣包括强化学习与机器博弈。目前已发表论文包括:
1. Qi Zhou, Houqiang Li, and Jie Wang. Deep Model-Based Reinforcement Learning via Estimated Uncertainty and Conservative Policy Optimization. In AAAI, 2020.
参考文献
[1] Qi Zhou, Houqiang Li, and Jie Wang. Deep Model-Based Reinforcement Learning via Estimated Uncertainty and Conservative Policy Optimization. In AAAI, 2020.
[2] Wenhao Yang, Xiang Li, and Zhihua Zhang. A regularized approach to sparse optimal policy in reinforcement learning. In NeurIPS, 2019.
[3] Tuomas Haarnoja, Aurick Zhou, Pieter Abbeel, and Sergey Levine. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In ICML, 2018.
[4] Tuomas Haarnoja, Haoran Tang, Pieter Abbeel, and Sergey Levine. Reinforcement learning with deep energy-based policies. In ICML, 2017.
[5] Tuomas Haarnoja, Aurick Zhou, Kristian Hartikainen, George Tucker, Sehoon Ha, Jie Tan, Vikash Kumar, Henry Zhu, Abhishek Gupta, Pieter Abbeel, et al. Soft actor-critic algorithms and applications. arXiv preprint, 2018.
[6] Yinlam Chow, Ofir Nachum, and Mohammad Ghavamzadeh. Path consistency learning in tsallis entropy regularized mdps. In ICML, 2018.
[7] Kyungjae Lee, Sungyub Kim, Sungbin Lim, Sungjoon Choi, and Songhwai Oh. Tsallis reinforcement learning: A unified framework for maximum entropy reinforcement learning. arXiv preprint, 2019.
[8] Geist, Matthieu, Bruno Scherrer, and Olivier Pietquin. A Theory of Regularized Markov Decision Processes. In ICML, 2018.
[9] Bogdan Mazoure, Thang Doan, Audrey Durand, R Devon Hjelm, and Joelle Pineau. Leveraging exploration in off-policy algorithms via normalizing flows. arXiv preprint, 2019.
[10] Yunhao Tang and Shipra Agrawal. Discretizing continuous action space for on-policy optimization. arXiv preprint, 2019.
[11] L Baringhaus and C Franz. Rigid motion invariant two-sample tests. Statistica Sinica, 2010.
[12] Scott Fujimoto, Herke Van Hoof, and David Meger. Addressing function approximation error in actor-critic methods. In ICML, 2018.
[13] Timothy P Lillicrap, Jonathan J Hunt, Alexander Pritzel, Nicolas Heess, Tom Erez, Yuval Tassa, David Silver, and Daan Wierstra. Continuous control with deep reinforcement learning. arXiv preprint, 2015.
更多阅读


#投 稿 通 道#
让你的论文被更多人看到
如何才能让更多的优质内容以更短路径到达读者群体,缩短读者寻找优质内容的成本呢?答案就是:你不认识的人。
总有一些你不认识的人,知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁,促使不同背景、不同方向的学者和学术灵感相互碰撞,迸发出更多的可能性。
PaperWeekly 鼓励高校实验室或个人,在我们的平台上分享各类优质内容,可以是最新论文解读,也可以是学习心得或技术干货。我们的目的只有一个,让知识真正流动起来。
📝 来稿标准:
• 稿件确系个人原创作品,来稿需注明作者个人信息(姓名+学校/工作单位+学历/职位+研究方向)
• 如果文章并非首发,请在投稿时提醒并附上所有已发布链接
• PaperWeekly 默认每篇文章都是首发,均会添加“原创”标志
📬 投稿邮箱:
• 投稿邮箱:hr@paperweekly.site
• 所有文章配图,请单独在附件中发送
• 请留下即时联系方式(微信或手机),以便我们在编辑发布时和作者沟通
🔍
现在,在「知乎」也能找到我们了
进入知乎首页搜索「PaperWeekly」
点击「关注」订阅我们的专栏吧
关于PaperWeekly
PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域,欢迎在公众号后台点击「交流群」,小助手将把你带入 PaperWeekly 的交流群里。