数据分析师应该知道的16种回归技术：线性回归

线性回归是最简单的回归方法。线性回归中的因变量通常为连续型数据，并假定自变量和因变量之间存在某种线性关系。当模型只有一个自变量和一个因变量，称之为简单线性回归或一元线性回归；当模型有一个应变量和多个自变量时，称之为多元线性回归或多变量线性回归。

多元线性回归一般定义为：

   

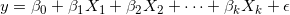
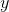
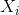
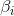
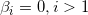
其中是因变量是自变量为误差项是回归系数，当时,多元线性回归退化为一元线性回归。

线性回归的基本假设

1. 自变量和因变量之间必须存在某种线性关系

2. 不能存在任何异常点

3. 没有异方差性

4. 样本观测值相互独立

5. 误差项服从均值为0方差为常数的正态分布

6. 不存在多重共线性

参数估计

为估计回归系数,我们基于最小二乘原则最小化误差项平方和，即

解上述等式，可得回归系数的估计值为：

线性回归在R中的实现

通过R软件基础包中lm函数可以很容易实现线性回归，关于lm函数的使用技巧:
为便于说明，假设有数据集 dt = data.frame (y , v1 , v2 , v3)

• 除去截距项 lm(y~v1+v2-1,data=dt) 或 lm( y ~ 0 + v1 +v2-1,data=dt)

• 包含数据集中除因变量之外的所有变量 lm(y~.,data=dt)

• 模型预测使用 predict(lmObject,newdata  =  newdt ) , 注意保持newdt数据结构和 lmObject一致，例如 lmObject = lm ( y ~ v2 + v3 ),则对应的newdt = data.frame (v2 = newv2, v3 = newv3)

• 与lm关联的函数：

  summary展示拟合模型的细节

  coefficients（）、coef（）列出拟合模型的参数（截距项和斜率）

  confint（）给出模型参数的置信（默认为95%）

  residuals（）列出拟合模型的残差值

  anova（）生成两个拟合模型的方差分析表

  plot（）生成评价拟合模型的诊断图

  predict（）用拟合模型对新数据集进行预测

案例

我们考虑datasets包中的swiss数据集合，该数据集包含47个观测值6个观测变量，分别是Fertility（生育率），Agriculture （农业人口中男性占比），Examination（士兵入伍考试获得最高分百分比），Education（小学以上学历百分比），Catho lic （天主教徒百分比），Infant（婴儿死亡率）。我们现在来探究生育率与其他因素之间的关系。

因此，70%的生育率变化可以通过线性回归来解释。

多重共线性检验可以

• 计算条件数kappa(X)，k<100,说明共线性程度小；如果100<k<1000，则存在较多的多重共线性;若k>1000，存在严重的多重共线性。

• 可以计算X矩阵的秩qr(X)$rank，如果不是满秩的，说明其中有Xi可以用其他的X的线性组合表示，不是特别准。

• 使用方差膨胀因子(VIF)，一般认为，当0<VIF<10，不存在多重共线性，当10≤VIF<100，存在较强的多重共线性，当VIF>=100，多重共线性非常严重。

结果表明swiss数据集中自变之间的多重共线性不严重。