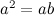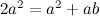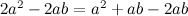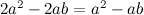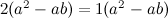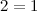你的逻辑真的可靠吗？

科学无国界

我们是知识的搬运工

福利时间

今天我们将送出由未读·探索家提供的优质科普书籍《登月使命：AR实境体验人类首次登月全过程》。

全景复原“人类的一大步”，满足你对登月的全部想象！

在这本书中，你能看到探月史上每一个重要的时刻，包括斯普特尼克1号升空、小狗莱卡进入太空、阿波罗11号登月、阿波罗13号脱险、宇航员谢泼德在月球上打高尔夫球……

本书融合了AR技术，用智能设备免费下载并安装配套App，按指示标扫描特定区域，你就能看到书中的珍贵档案动起来。你可以亲眼看到承担登月使命的航天器3D模型，亲耳听到宇航员从月球发来的祝福，亲自翻阅NASA解密档案……亲眼见证登月史上的每一个伟大瞬间！

只要你认真阅读下面的这篇文章，思考文末提出的问题，严格按照 互动： 你的答案 格式在评论区留言，就有机会获得奖品！

作者：Kona Macphee

翻译：Nothing 

审校：Nuor

什么是证明？哲学家已经就这个问题以及一件事如何才算被证明争论了多个世纪。毫无疑问，他们还将继续争论下去！另一方面，数学家长期以来使用“暂定的定义（working definitions）”来推动数学的进步。

以这个问题为开端，PASS Maths 已经发表了一系列文章来介绍证明和逻辑推理背后的基本思想以及它们在数学中的重要性。在这篇文章中，我们将对演绎推理进行简单介绍并且考察一下已知最早的数学证明之一。

演绎推理

给定一组已知或者被假定为真的命题，演绎推理是扩展这些命题的强有力的方法。在演绎推理中，我们认为如果前提P是已知或被假定为真的，那么我们可以得到结论C。例如，给定以下一些前提：

P：所有人都会死。

P：苏格拉底（Socrates）是人。

利用演绎推理，结论是：

C：苏格拉底会死。

在这个例子中，推理的原则是如果A蕴含B，且A为真，那么B也为真，中世纪哲学家称之为假言推理（modus ponens）。当然，演绎推理不是无懈可击的：推理的前提可能是错误的，推理的过程也可能是错误的！这就是为什么你有时候会做出错误的证明。例如，有多种方法可以证明1=2。下面是其中一个例子：

令a = b

有：

 

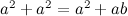
整理得：

两边同时除以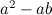得：

证毕。

你能指出证明中的漏洞吗？

如果结论无法从前提中得出，那么论证就是无效的，即便前提是正确的，我们也无法判断结论的真假。

如果论证是有效的但前提是错误的，那么我们同样无法判断命题真假，推理无法帮我们做出判断。

如果论证是有效的且前提是正确的，我们认为论证是可靠的且结论是正确的。从实用主义的观点来看，如果我们可以找到一个可靠的论证，我们就能认为证明了某件事。

以下表1给出了几种论证的形式， 表2给出了具体的例子：

表1 不同类型的演绎推理

	P不能推出C	P能推出C
P为假	无效	有效、不可靠
P为真	无效	有效、可靠

表2 一些演绎论点的例子

无效、错误前提 P：鱼是哺乳动物。 P:  鱼是温血动物。 C：哺乳动物是温血动物。	有效、不可靠 P: 哺乳动物是冷血动物。 P: 人是哺乳动物。 C：人是冷血动物。
无效、正确前提 P：鱼是冷血动物。 P：人类不是鱼。 C: 人类是温血动物。	有效、可靠 P: 人是温血动物。 P: 渔民是人。 C：渔民是温血动物。

在表格中，两个无效的论证不代表结论一定错误，只是无法从论证中得到判断。

开端：欧几里得几何

欧几里得出生在大约公元前365年的埃及亚历山大港，于约公元前300年去世。除了他在亚历山大港教授数学外，我们对他的生平知之甚少。欧几里得书写了大量著作，但是最有名的是他的《几何原本》，这是一本关于几何的著作并被当作教科书使用了超过2000年！这本书中的内容并不是欧几里得的原创，而是对当时的几何知识的总结。但是它们包含了数学史上最早的证明之一。

在《几何原本》中，欧几里得从描述点、线、平面、圆、钝角、锐角等的23条定义开始展开。欧几里得的定义既不正确也不错误，它们只是像字典一样解释着他要用到的术语的含义。然后他又写下了数条假设。其中五条并不限于几何，他称之为公理：

1、和同一个量相等的两个量也相等。

2、等量加等量，其和相等。

3、等量减等量，其差相等。

4、 彼此能够重合的几何图形是全等的。

5、整体大于部分。 

剩下五条假设和几何相关，他称之为公设：

1、两点可以决定一条直线。

2、直线可以沿其正反两个方向无限延长。

3、给定任意线段，可以以其一个端点作为圆心，该线段作为半径作一个圆。

4、凡直角都相等。

5、同一平面内一条直线和另外两条直线相交，若在这条直线同侧的两个内角之和小于180°，则另外两条直线一定相交。

这十条内容合在一起共同构成了欧氏几何的公理系统。公理指的是被假定为正确的逻辑原则，它无需被证明是正确的，它可以作为演绎推理的前提。

欧几里得的公理系统是利用演绎推理推导出其他内容的“第一性原理”。当然，所有的演绎论证只有在欧几里得公理和公设是正确时才是可靠的。

命题和证明

欧几里得在《几何原本》推导出大量几何命题并且用演绎推理展示了它们在他的公理体系内是正确的。

一个例子是命题6：“如果三角形中两个角相等，那么这两个角所对的边也相等。”

欧几里得的证明方法如下：

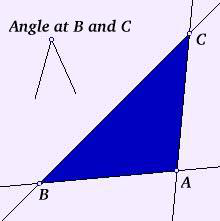
Figure 1: 命题6

“做三角形ABC且∠ABC等于∠ACB；那么边AB等于AC。假如AB不等于AC，其中一个会长于另一个。假设AB比较长；从AB中切下和AC等长的BD；连接DC。因为DB等于AC，而BC是公用的，DB等于AC，BC等于CB，且∠DBC等于∠ACB。

因此，DC等于AB，所以三角形DBC全等于三角形ACB，显然它们两个不一样大，因此出现了矛盾。所以只能是AB等于AC。“

欧几里得的公设是对的吗？

所有欧几里得时期的希腊人和后来的阿拉伯数学家都直觉的认为第五条公设实际上可以由五条公理和前四条公设推导出来。

许多人试图证明第五条公设，通常一个公认的证明在被证明有错之前会被长期接受。一般的，有瑕疵的证明会包含“循环论证”：不管怎样，他们先假定第五条公设是正确的来证明它是正确的

事实上，第五条公设无论对错，它都无法从其他公设和公理中推导出来。数学家长期着迷于第五条公设，但是直到十九和二十世纪我们才知道了第五条公设不成立的几何（非欧几何）。

在欧氏几何中，第五公设是对的。但是，在其他许多类型的几何中它是不对的。这是显而易见的，只要考虑球面上的几何就能看到。

在球面内是无法画一条真正的直线的，因此在球面几何中欧几里得关于线的想法变成了大圆。可以思考一下地球上的情形，经线都是一个大圆，赤道也是。事实上，球面上两点之间距离最短的路径就是这样一个大圆。

欧几里得前四条公设的一个推论是两条不同的直线相交，只能交于一点。在圆上，这个说法也有问题，因为不同的大圆总是交于两点！两条不同的经线都经过南极和北极！

但是请你记住，我们还没有说欧氏几何中的点在球面上对应什么！我们如果把相互对跖的两个点定义为球面上的一个点，问题就消失了。

根据欧几里得的第23个定义，“平行直线是在同一个平面内向两端无限延长不能相交的直线。”

按照这个定义，很容易看出欧几里得的前四条公设仍然成立。但是第五条公设失效，因为无法画出两条不相交的线。球面几何中没有平行线。

第五条公设失效的结果就是在球面上三角形内角和不再总是180度。事实上，有一个思维难题和非欧几何有关：

猎人离开家朝南走了一英里。然后朝西走了一英里并且射杀了一头熊，最后朝北走了一英里返回家里。问熊是什么颜色？

 欧几里得和演绎推理

关于欧氏几何的故事以及后来对非欧几何的发现，说明了利用公理进行演绎推理的好处和缺点。

利用定义、公理和公设作为一个系统。欧几里得可以通过演绎推理得到大量的几何命题，他的公理和证明在数个世纪中成为数学家们有用的工具，并且展示了演绎推理的威力。

然而，发现非欧几何漫长又痛苦的过程展示了演绎推理的局限性：公理系统中的所有证明都不能超出公理系统自身。在欧氏平面中，欧几里得第五公设是对的，他的证明既有效又可靠。然而在非欧几何中，例如球面几何，第五公设就是错的，因此欧几里得的证明是不可靠的。

原文来源：

https://plus.maths.org/content/origins-proof#Appendix

互动问题

【互动问题：你遇到过哪些奇葩又无法反驳的逻辑？】

请大家严格按照  互动：问题答案  的格式在评论区留言参与互动，格式不符合要求者无效。

截止到本周四中午12点，点赞数前三名的朋友将获得我们送出的图书一本。

编辑：loulou
近期热门文章Top10
↓ 点击标题即可查看 ↓
1. 为什么品客薯片不容易碎，但乐事薯片容易碎？
2. 学物理能做什么？
3. 听说高考数学全国卷三考了朵云……
4. 6÷2(1+2) 到底等于 1 还是 9？
5. 可达鸭为啥脑壳痛？
6. 两千多度时，冰变成了黑色
7. 4.6692……：一个比圆周率更神秘的常数
8. 人类突然消失之后，世界会变成什么样子？
9. 为什么洗澡水砸不死蚊子？
10. 中国哪里的地铁最拥挤
点此查看以往全部热门文章