卡尔曼滤波器及其在航空航天中的应用

2017 年 8 月 31 日 无人机 党朝辉

感谢未来空天公众号授权转载

编者按：2017年9月份最新一期JGCD期刊推出了专刊：“卡尔曼滤波器及其在航空航天中的应用”。这一期专题是用于纪念去年7月刚刚过世的卡尔曼博士。卡尔曼博士在上世纪60年代提出了至今被广为使用的卡尔曼滤波算法。这一算法在很多工程领域尤其是航空航天领域取得了难以估量的实用价值，因此被当今学者所津津乐道。JGCD期刊客座主编就此撰写了一篇介绍性短文，在这篇短文里回顾了卡尔曼博士取得这一杰出成就的简要历史背景。由于原文比较精彩，现翻译如下以飨读者。

卡尔曼滤波器及其在航空航天中的应用

原文 | John L. Crassidis

翻译 | 党朝辉

2016年7月2日，制导、导航与控制（GN&C）领域失去了一位杰出的大师鲁道夫·埃米尔·卡尔曼博士（Dr. Rudolf Emil Kalman）。尽管卡尔曼博士在一般控制和估计理论等领域都做出了卓越的贡献，但他最大的成就是在1960年发表了世界上第一篇有关“卡尔曼滤波器”的论文。由于这项先驱性的工作，他被授予很多崇高的奖项，并因此入选美国国家科学院院士、美国国家工程院院士以及美国艺术与科学院院士。2009年的时候，卡尔曼博士得到了奥巴马总统授予的国家科学奖章，这是美国政府颁发给科学家的最高荣誉。为纪念卡尔曼博士，制导、控制与动力学期刊（JGCD）曾在2016年发出专题征文通知，主题为“卡尔曼滤波器在航空航天领域的应用”。一年以后的现在，我们很高兴地通知大家这个专题已经在这个月（译者注：9月份）的JGCD期刊出版了。

众所周知，很多有关序列滤波问题的独立研究都可以追溯到卡尔曼的那篇影响深远的论文——“一种线性滤波和预测问题的新方法”（A new approach to linear filtering and prediction problems,Transactions of the ASME-Journal of Basic Engineering, Vol.82, Series D, 1960,pp.35-45）。历史上最早的有关滤波问题的研究是20世纪30年代末到40年代初由柯尔莫戈洛夫（Kolmogorov）和科瑞恩（Krein）所做的原创性工作，以及维纳（Wiener）于同时期所做的整理和分类工作。1958年，斯特拉托诺维奇（Ruslan L. Stratonovich）博士在有关统计放射物理学的全联盟会议上发表了他关于条件马尔科夫过程以及相关的非线性滤波问题的初步结果。但是，这个理论的实用价值很难被人理解，甚至理论本身由于现已为人们熟知的“斯特拉托诺维奇积分”的引入而存在很多争议。其他人也在1950年代末到1960年代初研究不同形式的卡尔曼滤波器。例如，据Leonard A. McGee 和Stanley F.Schmidt 博士说，1985年的NASA技术备忘录86847号文件（题目是“作为一种实用工具用于航空航天和工业领域的卡尔曼滤波器的发现”）里记载了“Richard Battin博士在不熟悉卡尔曼的工作的情况下曾独立开展了类似的研究”。关于Battin博士的历史贡献特别是在阿波罗登月任务中的贡献的杰出总结，可以在JGCD创立者中的一位客座编辑Donald C.Fraser一篇题为“我所认识的Battin”（JGCD，Vol.38, 2015, pp.1546-1547）中发现。1961年9月，Battin博士发表了一篇仪器仪表实验室报告，题目是“用于空间飞行的一种统计最优导航算法”。在这篇报告中，他做了如下陈述：

“以迭代操作方式实施的最优线性估计，即在这种迭代过程中当前的最优估计与最新获得的信息相混合从而生成了更好的估计，它的创立者是卡尔曼。我非常感激Stanley F. Schmidt博士，由于他的缘故我把自己的注意力转移到了卡尔曼杰出的工作上了。实际上，卡尔曼理论最早在空间导航上的应用正是由Schmidt以及他的同事完成的。不过本文下述几节所描述的研究是在不知道Schmidt相关工作的详细情况的前提下完成的……”

卡尔曼1960年的开创性论文从概率论的角度推导了线性离散时间滤波器的结构，这是被我们今天正式命名为卡尔曼滤波器的第一篇正式论文。其余的都是历史。

自从那时候以来，卡尔曼滤波器被用在了很多领域。这些领域包括运载器跟踪（包括大气层中的、太空中的、地面的、水下的）、自主一体化导航、时间序列分析(例如信号处理和计量经济学)、数字图像处理，等等。自阿波罗太空任务的导航系统用了卡尔曼滤波器以来，该算法在航空航天中的应用主要集中在飞行器和航天器的跟踪与导航上。大部分现有的GPS/惯导系统都把扩展卡尔曼滤波器作为数据融合的算法，从而通过使用GPS信号和惯性测量单元（IMU，包括陀螺仪和加速度计）的数据作为测量值估计位置和姿态以及它们的时间导数，同时还用于校准IMU的相关参数。卡尔曼滤波器时至今日仍是现代航天任务中的核心算法，它已经被用于“新地平线”（New Horizons）任务，主要是平滑它飞向冥王星的轨迹。

本专题的主要目的在于集中展示一批涉及卡尔曼滤波器的新颖的航空航天GN&C应用。这一期的技术部分包括了来自全世界的27篇全文（full-length paper）和短文（engineering note）。这些论文涉及的主题非常宽泛，包括了航天器和飞机导航、姿态估计和分析、轨道估计、目标跟踪、振动分析、空气弹性变形飞机的控制，以及大气热定位估计。征稿过程中其实收到了大量投稿，但是它们因为主题不是特别相关而没有包含进来。这一期专题论文是JGCD期刊有史以来最大的一期，但是受限于容量不得已还是缩小了主题范围。无论一篇论文是否被我们包含进来，我们都非常感谢作者的热情和努力。最后，我们特别感谢所有腾出时间进行高质量审稿的专家学者。我们非常感激那些长期致力于将卡尔曼博士的研究应用于航空航天领域并取得重大成功的个人!

客座编辑：John L. Crassidis

扩展阅读：卡尔曼滤波器

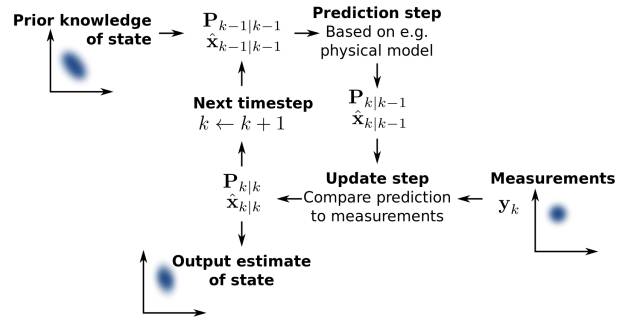
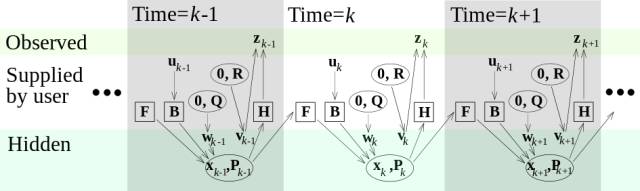
卡尔曼滤波器是一种针对动力学系统的线性递推状态估计算法，其基本模型及递推过程如下图1和图2所示。