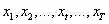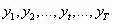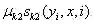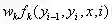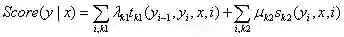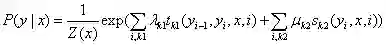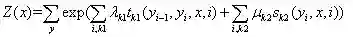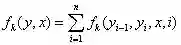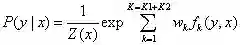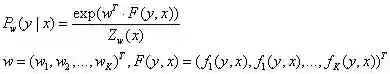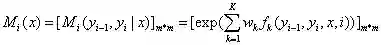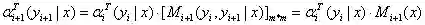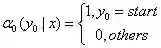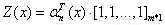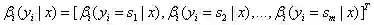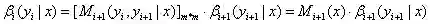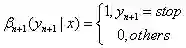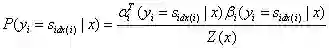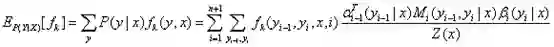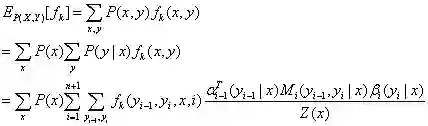NLP硬核入门-条件随机场CRF
1 CRF概述
1.1随机场的定义
在这一小节,我们将会由泛化到特例,依次介绍随机场、马尔科夫随机场、条件随机场、线性链条件随机场的概念。
(1)随机场是一个图模型,是由若干个结点(随机变量)和边(依赖关系)组成的图模型,当给每一个结点按照某种分布随机赋予一个值之后,其全体就叫做随机场。
(2)马尔科夫随机场是随机场的特例,它假设随机场中任意一个结点的赋值,仅仅和它的邻结点的取值有关,和不相邻的结点的取值无关。用学术语言表示是:满足成对、局部或全局马尔科夫性。
(3)条件随机场CRF是马尔科夫随机场的特例,它假设模型中只有X(输入变量,观测值)和Y(输出变量,状态值)两种变量。输出变量Y构成马尔可夫随机场,输入变量X不具有马尔科夫性。
(4)线性链条件随机场,是状态序列是线性链的条件随机场。
注1:马尔科夫性:随机过程中某事件的发生只取决于它的上一事件,是“无记忆”过程。
我们的应用领域是NLP,所以本文只针对线性链条件随机场进行讨论。
线性链条件随机场有以下性质:
(1)对于状态序列y,y的值只与相邻的y有关系,体现马尔科夫性。
(2)任意位置的y与所有位置的x都有关系。
(3)我们研究的线性链条件随机场,假设状态序列Y和观测序列X有相同的结构,但是实际上后文公式的推导,对于状态序列Y和观测序列X结构不同的条件随机场也适用。
(4)观测序列X是作为一个整体,去影响状态序列Y的值,而不是只影响相同或邻近位置(时刻)的Y。
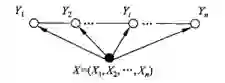
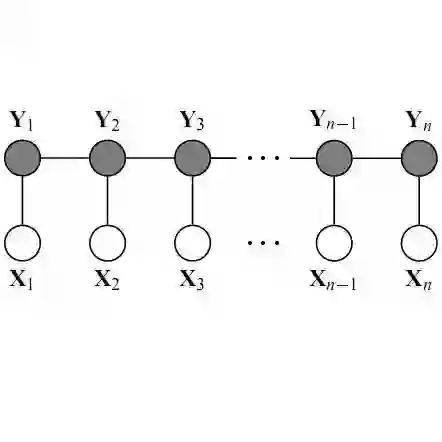
(5)线性链条件随机场的示意图如下:
注二:李航老师的《统计学习方法》里,使用了两种示意图来描述线性链条件随机场,一种是上文所呈现的,这张图更能够体现性质(4),另一种如下图,关注点是X和Y同结构:
1.2CRF的应用
线性链条件随机场CRF是在给定一组随机变量X(观测值)的条件下,获取另一组随机变量Y(状态值)的条件概率分布模型。在NLP领域,线性链条件随机场被广泛用于标注任务(NER、分词等)。
1.3 构建CRF的思路(重要)
我们先给出构建CRF模型的核心思路,现在暂不需要读懂这些思路的本质思想,但是我们要带着这些思路去阅读后续的内容。
(1)CRF是判别模型,是黑箱模型,不关心概率分布情况,只关心输出结果。
(2)CRF最重要的工作,是提取特征,构建特征函数。
(3)CRF使用特征函数给不同的标注网络打分,根据分数选出可能性最高的标注网络。
(4)CRF模型的计算过程,使用的是以e为底的指数。这个建模思路和深度学习输出层的softmax是一致的。先计算各个可能情况的分数,再进行softmax归一化操作。
2 CRF模型的概率计算
(对数学公式推导没兴趣的童鞋,只需要看2.1和2.2)
2.1 标记符号和参数
先约定一下CRF的标记符号:
观测值序列:
状态值序列:
转移(共现)特征函数及其权重:
状态(发射)特征函数及其权重:
简化后的特征函数及其权重:
特征函数t的下标:k1
特征函数s的下标:k2
简化后的特征函数f的下标:k
2.2 一个栗子
在进行公式推导前,我们先通过一个直观的例子,初步了解下CRF。
例:输入观测序列为X=(x1,x2,x3),输出状态序列为Y=(y1,y2,y3),状态值集合为{1,2}。在已知观测序列后,得到的特征函数如下。求状态序列为Y=(y1,y2,y3)=(1,2,2)的非规范化条件概率。
解:参照状态序列取值和特征函数定义,可得特征函数t1,t5,s1,s2,s4取值为1,其余特征函数取值为0。乘上权重后,可得状态序列(1,2,2)的非规范化条件概率为:1+0.2+1+0.5+0.5=3.2
2.3特征函数
在这一小节,我们描述下特征函数,以及它的简化形式和矩阵形式。
(1)线性链条件随机场的原始参数化形式
分数:
归一化概率:
其中,归一项为:
t为定义在边上的特征函数,通常取值0或1,依赖于两个相邻结点的状态,λ为其权重。t有时被称为转移特征,其实称为共现特征更合适些。因为图模型更强调位置关系而不是时序关系。
s为定义在节点上的特征函数,通常取值0或1,依赖于单个结点的状态,μ为其权重。s有时被称为状态特征。
需要强调的是:CRF模型中涉及的条件概率,不是真实的概率,而是通过分值softmax归一化成的概率。
(2)线性链条件随机场的简化形式
特征函数:
权重:
对特征函数在各个位置求和,将局部特征函数转化为全局特征函数:
归一化概率:
向量化:
(3)线性链条件随机场的矩阵形式
构建矩阵Mi(x)。位置i和观测值序列x是矩阵的自变量。
矩阵的维度是m*m,m为状态值y的集合的元素个数,矩阵的行表示的是位置i-1的状态,矩阵的列表示的是位置i的状态,矩阵各个位置的值表示位置i-1状态和位置i状态的共现分数,并以e为底取指数。
2.4 前向后向算法
(1)前向算法模型
(a)αi(yi=s|x)表示状态序列y在位置i取值s,在位置1~i取值为任意值的可能性分数的非规范化概率。
定义:
(b)递归公式:
(c)人为定义:
(d)归一项:
(2)后向算法模型
(a)βi(yi=s|x)表示状态序列y在位置i取值s,在位置i+1~n取值为任意值的可能性分数的非规范化概率。
定义:
(b)递归公式:
(c)人为定义:
(d)归一化项:
注:在前向算法和后向算法中,人为地定义了α(0)和β(n+1),采用的是李航老师书里的定义方法。但是,我认为采用先验概率(类似HMM中的初始概率分布)或者全部定义成1更合适。因为这里的概率模型应该表现得更通用一点,而不要引入实际预测序列的第一项和最后一项的信息。
2.5 一些概率和期望的计算
(1)两个常用的概率公式
状态序列y,位置i的取值为特定值,其余位置为任意值的可能性分数的归一化条件概率:
状态序列y,位置i-1,i的取值为特定值,其余位置为任意值的可能性分数的归一化条件概率:
(1)两个常用的期望公式
特征函数f关于条件分布P(Y|X)的数学期望:
特征函数f关于联合分布P(X,Y)的数学期望:
3 CRF模型的训练和预测
3.1学习训练问题
CRF模型采用正则化的极大似然估计最大化概率。
采用的最优化算法可以是:迭代尺度法IIS,梯度下降法,拟牛顿法。
相应的知识可以通过最优化方法的资料进行学习,本文篇幅有限,就不作展开了。
3.2预测解码问题
和HMM完全一样,采用维特比算法进行预测解码,这里不作展开。
4 CRF的优缺点(重要)
4.1CRF相对于HMM的优点
(1)规避了马尔科夫性(有限历史性),能够获取长文本的远距离依赖的信息。
(2)规避了齐次性,模型能够获取序列的位置信息,并且序列的位置信息会影响预测出的状态序列。
(3)规避了观测独立性,观测值之间的相关性信息能够被提取。
(4)不是单向图,而是无向图,能够充分提取上下文信息作为特征。
(5)改善了标记偏置LabelBias问题,因为CRF相对于HMM能够更多地获取序列的全局概率信息。
(6)CRF的思路是利用多个特征,对状态序列进行预测。HMM的表现形式使他无法使用多个复杂特征。
4.2条件随机场CRF的缺点
(1)CRF训练代价大、复杂度高。
(2)每个特征的权重固定,特征函数只有0和1两个取值。
(3)模型过于复杂,在海量数据的情况下,业界多用神经网络。
(4)需要人为构造特征函数,特征工程对CRF模型的影响很大。
(5)转移特征函数的自变量只涉及两个相邻位置,而CRF定义中的马尔科夫性,应该涉及三个相邻位置。
4.3标记偏置LabelBias
在HMM中的体现:对于某一时刻的任一状态,当它向后一时进行状态刻转移时,会对转移到的所有状态的概率做归一化,这是一种局部的归一化。即使某个转移概率特别高,其转移概率也不超过1。即使某个转移概率特别低,如果其它几个转移概率同样低,那么归一化后的转移概率也不会接近0。
在CRF被规避的原因:CRF使用了全局的归一化。在进行归一化之前,使用分数来标记状态路径的可能性大小。待所有路径所有位置的分数都计算完成后,再进行归一化。某些某个状态转移的子路径有很高的分数,会对整条路径的概率产生很大的影响。
5 基于TensorFlow的BiLSTM-CRF
BiLSTM-CRF是当前用得比较广泛的序列标注模型。
BiLSTM-CRF模型由BiLSTM和CRF两个部分组成。
BiLSTM使用的是分类任务的配置,最终输出一个标注好的序列。也就是说,即使没有CRF,BiLSTM也能独立完成标注任务。
CRF接收BiLSTM输出的标注序列,进行计算,最后输出修正后的标注序列。
TensorFlow提供了CRF的开发包,路径为:tf.contrib.crf。需要强调的是,TensorFlow的CRF,提供的是一个严重简化后的CRF,和原始CRF差异较大。虽然减小了模型复杂度,但是在准确率上也一定会有所损失。
下面简要介绍下TensorFlow中CRF模块的几个关键函数。
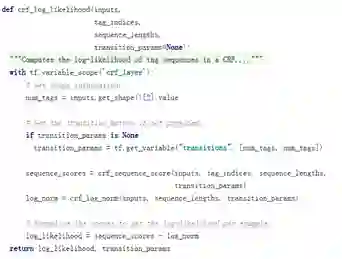
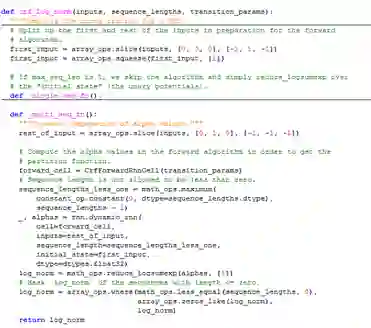
(1)crf_log_likelihood
BiLSTM模块输出的序列,通过参数inputs输入CRF模块。
CRF模块通过crf_sequence_score计算状态序列可能性分数,通过crf_log_norm计算归一化项。
最后返回log_likelihood对数似然。
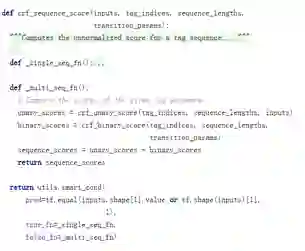
(2)crf_sequence_score
crf_sequence_score通过crf_unary_score计算状态特征分数,通过crf_binary_score计算共现特征分数。
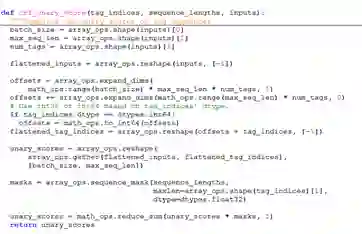
(3)crf_unary_score
crf_unary_score利用掩码的方式,计算得出一个类似交叉熵的值。
(4)crf_binary_score
crf_binary_score构造了一个共现矩阵transition_params,表示不同状态共现的概率,这个矩阵是可训练的。最后通过共现矩阵返回共现特征分数。
(5)crf_log_norm
归一化项。
知乎文章地址:
https://zhuanlan.zhihu.com/p/87638630
由于微信公众号文章有修改字数的限制,故本文后续的纠错和更新将呈现在知乎的同名文章里。
参考文献
[1] 李航 统计学习方法 清华大学出版社
[2] 条件随机场CRF(一/二/三) 刘建平Pinard https://www.cnblogs.com/pinard/p/7048333.html
本文转载自公众号:数论遗珠,作者:阮智昊
推荐阅读
关于AINLP
AINLP 是一个有趣有AI的自然语言处理社区,专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享,主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等,欢迎关注!加技术交流群请添加AINLP君微信(id:AINLP2),备注工作/研究方向+加群目的。