分类问题统计指标入门：混淆矩阵、召回、误检率、AUROC

来源：StackExchange

编译：weakish

编者按：当比较多个不同模型的表现时，仅仅考虑精确度（accuracy）往往是不够的。常用的指标还包括混淆矩阵、召回、误检率和AUROC。Adobe Research研究科学家Franck Dernoncourt在Cross Validated上简明清晰地介绍了这些概念。

缩写

• AUC 曲线下面积（Area Under the Curve）

• AUROC 接受者操作特征曲线下面积（Area Under the Receiver Operating Characteristic curve）

大多数时候，AUC都是指AUROC，这是一个不好地做法，正如Marc Claesen指出的那样，AUC有歧义（可能是任何曲线），而AUROC没有歧义。

AUROC解释

AUROC有一些等价的解释：

• 均匀抽取的随机阳性样本排名在均匀抽取的随机阴性样本之前的期望

• 阳性样本排名在均匀抽取的随机阴性样本之前的期望比例

• 若排名在一个随机抽取的随机阴性样本前分割，期望的真阳性率

• 阴性样本排名在均匀抽取的随机阳性样本之后和期望比例

• 若排名在一个均匀抽取的随机阳性样本后分割，期望的假阳性率

更多阅读：如何推导AUROC的概率解释（https://stats.stackexchange.com/questions/180638/how-to-derive-the-probabilistic-interpretation-of-the-auc/277721#277721）

AUROC计算

假设我们有一个概率二元分类器，比如逻辑回归。

在讨论ROC曲线（接受者操作特征曲线）之前，我们需要理解混淆矩阵（confusion matrix）的概念。一个二元预测可能有4个结果：

• 我们预测0，而真实类别是0：这被称为真阴性（True Negative），即，我们正确预测类别为阴性（0）。比如，杀毒软件没有将一个无害的文件识别为病毒。

• 我们预测0，而真实类别是1：这被称为假阴性（False Negative），即，我们错误预测类别为阴性（0）。比如，杀毒软件没有识别出一个病毒。

• 我们预测1，而真实类别是0：这被称为假阳性（False Positive），即，我们错误预测类别为阳性（1）。比如，杀毒软件将一个无害的文件识别为病毒。

• 我们预测1，而真实类别是1：这被称为真阳性（True Positive），即，我们正确预测类别为阳性（1）。比如，杀毒软件正确地识别出一个病毒。

我们统计模型做出的预测，数一下这四种结果各自出现了多少次，可以得到混淆矩阵：

在上面的混淆矩阵示例中，在分类的50个数据点中，45个分类正确，5个分类错误。

当比较两个不同模型的时候，使用单一指标常常比使用多个指标更方便，下面我们基于混淆矩阵计算两个指标，之后我们会将这两个指标组合成一个：

• 真阳性率（TPR），即，灵敏度、命中率、召回，定义为TP/(TP+FN)。从直觉上说，这一指标对应被正确识别为阳性的阳性数据点占所有阳性数据点的比例。换句话说，TPR越高，我们遗漏的阳性数据点就越少。

• 假阳性率（FPR），即，误检率，定义为FP/(FP+TN)。从直觉上说，这一指标对应被误认为阳性的阴性数据点占所有阴性数据点的比例。换句话说，FPR越高，我们错误分类的阴性数据点就越多。

为了将FPR和TPR组合成一个指标，我们首先基于不同的阈值（例如：0.00; 0.01, 0.02, …, 1.00）计算前两个指标的逻辑回归，接着将它们绘制为一个图像，其中FPR值为横轴，TPR值为纵轴。得到的曲线为ROC曲线，我们考虑的指标是该曲线的AUC，称为AUROC。

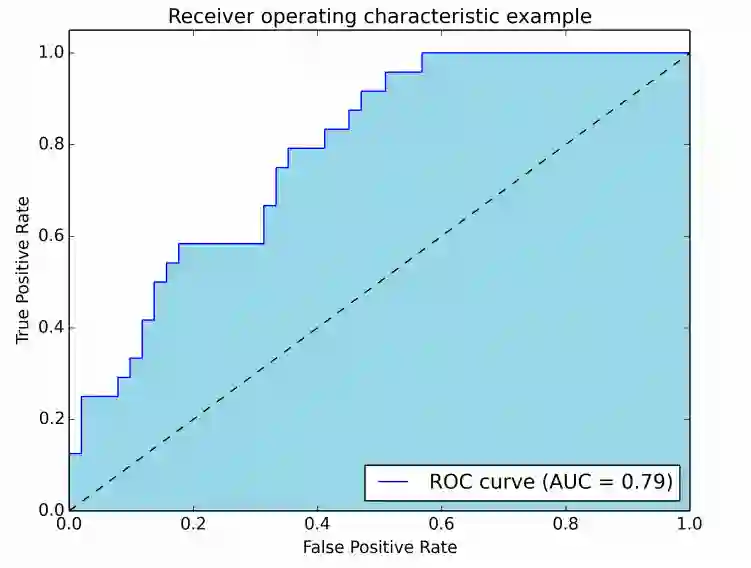
下图展示了AUROC的图像：

在上图中，蓝色区域对应接受者操作特征曲线（AUROC）。对角虚线为随机预测器的ROC曲线：AUROC为0.5. 随机预测器通常用作基线，以检验模型是否有用。

如果你希望得到一些第一手的经验：

• Python: http://scikit-learn.org/stable/auto_examples/model_selection/plot_roc.html

• MATLAB: http://www.mathworks.com/help/stats/perfcurve.html

原文地址：https://stats.stackexchange.com/questions/132777/what-does-auc-stand-for-and-what-is-it/132832#132832