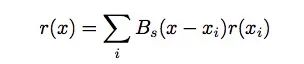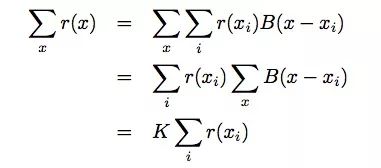证伪：CNN中的图片平移不变性

2018 年 6 月 12 日 论智

来源：arXiv

编译：Bot

编者按：今天论智给大家带来的论文是希伯来大学的Aharon Azulay和Yair Weiss近期发表的Why do deep convolutional networks generalize so poorly to small image transformations? 这篇文章发现当小尺寸图像发生平移后，CNN会出现识别错误的现象，而且这一现象是普遍的。

摘要

通常我们认为深度CNN对图像的平移、形变具有不变性，但本文却揭示了这样一个现实：当图像在当前平面上平移几个像素后，现代CNN（如VGG16、ResNet50和InceptionResNetV2）的输出会发生巨大改变，而且图像越小，网络的识别性能越差；同时，网络的深度也会影响它的错误率。

论文通过研究表明，产生这个现象的主因是现代CNN体系结构没有遵循经典采样定理，无法保证通用性，而常用图像数据集的统计偏差也会使CNN无法学会其中的平移不变性。综上所述，CNN在物体识别上的泛化能力还比不上人类。

CNN的失误

深度卷积神经网络（CNN）对计算机视觉带来的革新是天翻地覆的，尤其是在物体识别领域。和其他机器学习算法一样，CNN成功的关键在于归纳偏差的方法，不同架构的选择影响着偏差的具体计算方式。在CNN中，卷积和池化这两个关键操作是由图像不变性驱动的，这意味如果我们对图像做位移、缩放、变形等操作，它们对网络提取特征没有影响。

但事实真的如此吗？

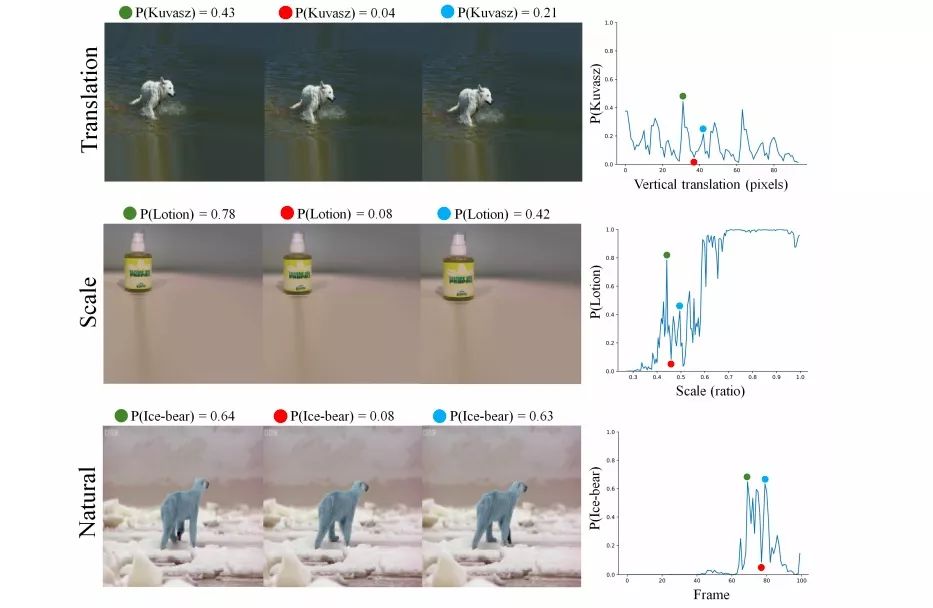
在上图中，左侧图像是模型的输入，右侧折线图是模型评分，使用的模型是InceptionResNet-V2 CNN。可以发现，作者在这里分别对图像做了平移、放大和微小形变。在最上方的输入中，他们只是将图像从左到右依次下移了一像素，就使模型评分出现了剧烈的波动；在中间的输入中，图像被依次放大，模型的评分也经历了直线下降和直线上升；而对于最下方的输入，这三张图是从BBC纪录片中选取的连续帧，它们在人类眼中是北极熊的自然运动姿态，但在CNN“眼中”却很不一样，模型评分同样遭遇“滑铁卢”。

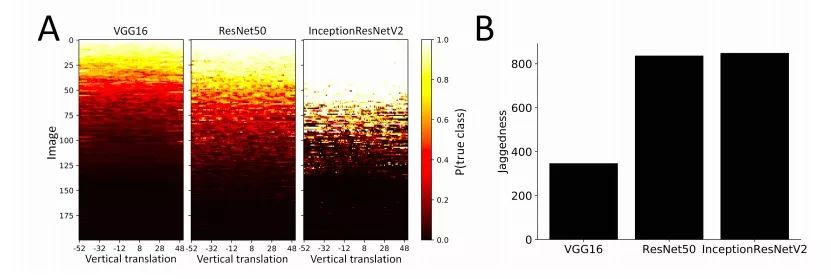
为了找出导致CNN失误的特征，他们又从ImageNet验证集中随机选择了200幅图像，并把它们嵌入较大的图像中做系统性平移，由图像平移导致的空白区域已经用程序修补过了，在这个基础上，他们测试了VGG16、ResNet50和InceptionResNetV2三个现代CNN模型的评分，结果如下：

图A的纵坐标是200张图像，它用颜色深浅表示模型识别结果的好坏，其中非黑色彩表示模型存在能对转变后的图像正确分类的概率，全黑则表示完全无法正确分类。通过观察颜色变化我们可以发现，无论是VGG16、ResNet50还是InceptionResNetV2，它们在许多图片上都显示出了由浅到深的突然转变。

论文作者在这里引入了一种名为jaggedness的量化标准：模型预测准确率top-5类别中的图像，经历一次一像素平移就导致分类错误（也可以是准确率低一下子变成准确率高）。他们发现平移会大幅影响输出的图片占比28%。而如图B所示，相对于VGG16，ResNet50和InceptionResNetV2因为网络更深，它们的“jaggedness”水平更高。

那么，这是为什么呢？

对采样定理的忽略

CNN的上述失误是令人费解的。因为从直观上来看，如果网络中的所有层都是卷积的，那当网络对图像编码时，所有表征应该也都跟着一起被编码了。这些特征被池化层逐级筛选，最后提取出用于分类决策的终极特征，理论上来说，这些特征相对被编码的表征应该是不变的。所以问题在哪儿？

这篇论文提出的一个关键思想是CNN存在采样缺陷。现代CNN中普遍包含二次采样（subsampling）操作，它是我们常说的降采样层，也就是池化层、stride。它的本意是为了提高图像的平移不变性，同时减少参数，但它在平移性上的表现真的很一般。之前Simoncelli等人已经在论文Shiftable multiscale transforms中验证了二次采样在平移不变性上的失败，他们在文中说：

我们不能简单地把系统中的平移不变性寄希望于卷积和二次采样，输入信号的平移不意味着变换系数的简单平移，除非这个平移是每个二次采样因子的倍数。

考虑到现在CNN通常包含很多池化层，它们的二次采样因子会非常大，以InceptionResnetV2为例，这个模型的二次采样因子是45，所以它保证精确平移不变性的概率有多大？只有1/45²。

下面我们从计算角度看看其中的猫腻：

我们设r(x)是模型在图像x处获得的特征信号，如果把图像平移δ后，模型获得的还是同样的特征信号，那我们就称这个信号是“卷积”的。注意一点，这个定义已经包含输入图像进入filter提取特征信号等其他线性操作，但不包括二次采样和其他非线性操作。

观察

如果r(x)是卷积的，那么全局池化后得到的特征信号 r = ∑_xr(x) 应该具有平移不变性。

证明

以下论证来自之前我们对“卷积”的定义。如果r(x)是图像x处的特征信号，而r₂(x)是同一图像平移后的特征信号，那么 ∑_xr(x) = ∑_xr₂(x) 成立，因为两者是平移前后的特征信号，是不变的。

定义

对于特征信号r(x)和二次采样因子s，如果信号中x处的任意输出x是采样网格的线性插值：

那么我们就认为r(x)是“可位移的”（shiftable）。因为参照之前图像位移的说法，既然采样后信号具有平移不变性，那原信号载体就是可以移动的。其中x_i是二次采样因子s采样网格上的信号，B_s(x)是从采样中重建的r(x)基函数。

经典Shannon-Nyquist定理告诉我们，当且仅当采样频率是r(x)最高频率的两倍时，r(x)才可以位移。

论点

如果r(x)可以位移，那么采样网格全局池化后得到的最终特征信号 r = ∑_ir(x_i) 应该具有平移不变性。

证明

通过计算我们发现了这么一个事实：采样网格上的全局池化就相当于所有x的全局池化：

其中，K = ∑_xB(x − x_i)和K与x_i无关。

而现代CNN的二次采样忽视了以上这些内容，所以平移不变性是难以保证的。

为什么CNN不能从数据中学习平移不变性？

虽然上一节论证了CNN在架构上就无法保证平移不变性，但为什么它就不能从大量数据里学到不变性呢？事实上，它确实能从数据中学到部分不变性，那么问题还出在哪儿？

论文的观点是数据集里的图像自带“摄影师偏差”，很可惜论文作者做出的解释很糟糕，一会儿讲分布，一会儿讲数据增强，非常没有说服力。但是这个观点确实值得关注，心理学领域曾有过关于“摄影师偏差”对人类视角影响的研究，虽然缺乏数据集论证，但很多人相信，同样的影响也发生在计算机视觉中。

这里我们引用Azulay和Weiss的两个更有说服力的点：

CIFAR-10和ImageNet的图片存在大量“摄影师偏差”，这使得神经网络无需学会真实的平移不变性。宏观来看，只要不是像素级别的编码，世界上就不存在两张完全一样的图像，所以神经网络是无法学到严格的平移不变性的，也不需要学。
例如近几年提出的群卷积，它包含的filter数量比其他不变性架构更少，但代价是filter里参数更多，模型也更不灵活。如果数据集里存在“摄影师偏差”，那现有不变性架构里的参数是无法描述完整情况的，因此它们只会获得一个“模糊”的结果，而且缺乏灵活性，性能自然也比非不变性架构要差不少。