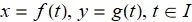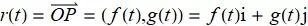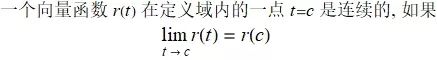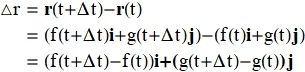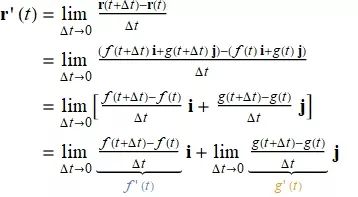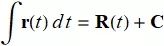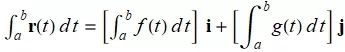【向量值函数】图解高等数学-下 02

9.3 向量 - 值函数

平面曲线

当一个质点在时间区间 I 在平面内运动时, 可以把质点的坐标看做在 I 上的函数

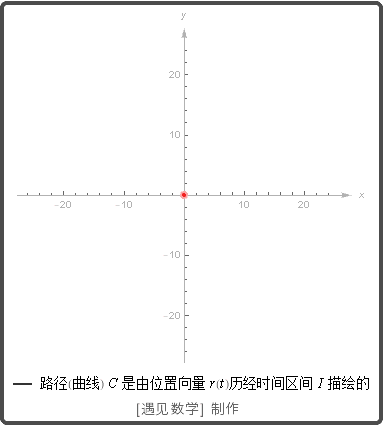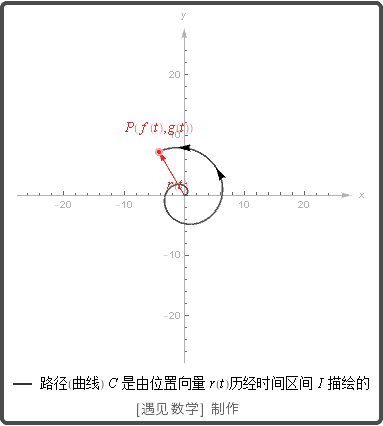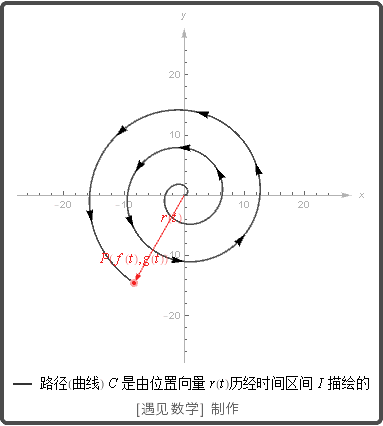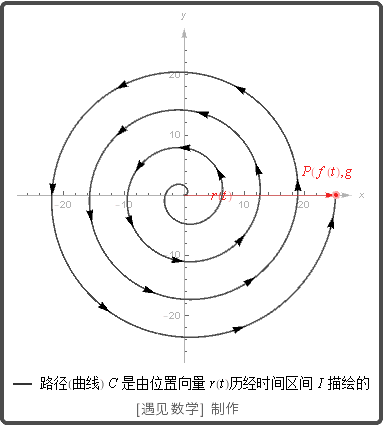
点(x,y) = (f(t), g(t)) 形成平面上的曲线, 称它为质点的路径. 从原点到质点在时刻 t 的位置 P(f(t),g(t)) 的向量

是质点的位置向量, 函数 f 和 g 是位置向量的分量函数(分量). 质点的路径是在时间区间 I 由 r 绘制的曲线. 观察下面的向量函数

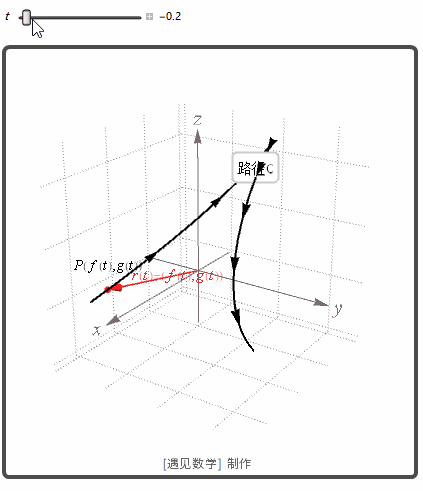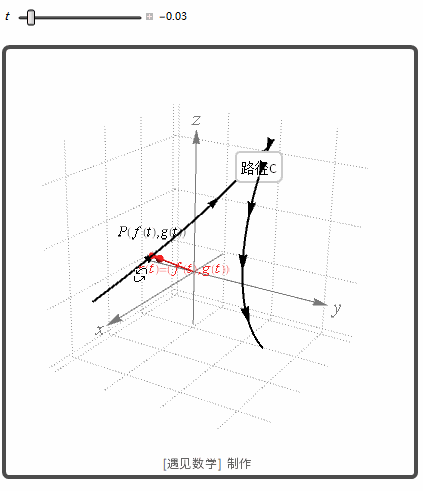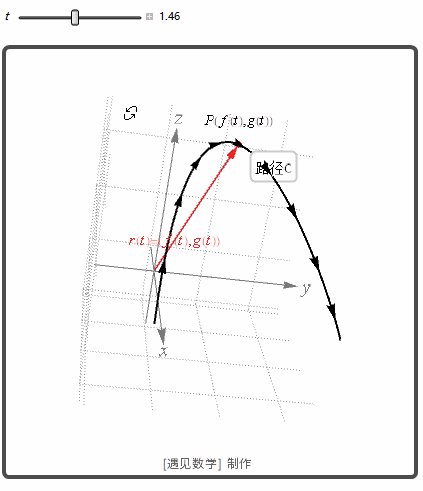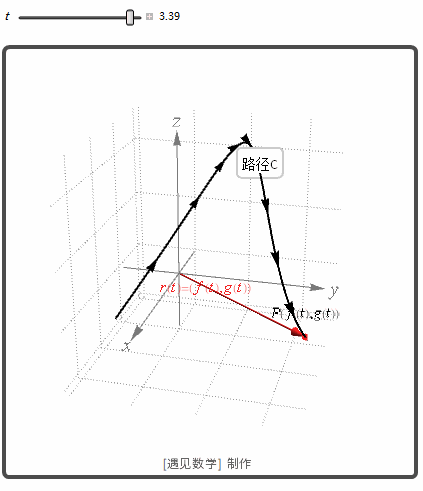
三维空间中的向量函数:

极限和连续

通过数值分量来定义向量函数的极限.

在一点的连续性

导数

假定 r(t)=f(t)i+g(t)j 是沿一平面曲线运动的质点的位置向量, 而 f 和 g 是 t 的可微函数. 则质点位置再时刻 $\text{t+}△\text{x}$ 和时刻 t 的差是$△\text{r=r(t+}△\text{t)-r(t)}$, 用分量表示为:

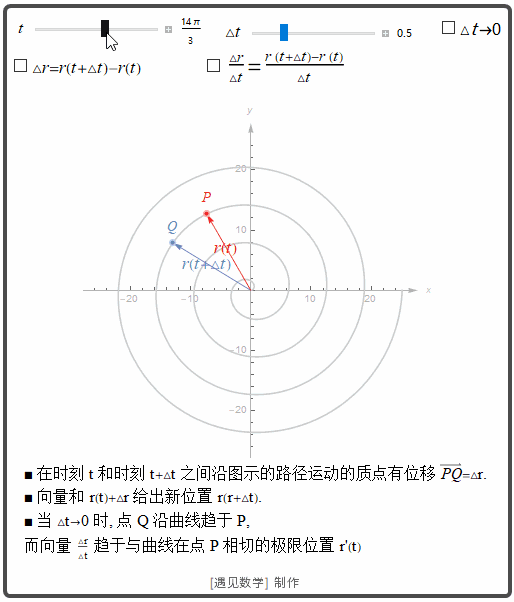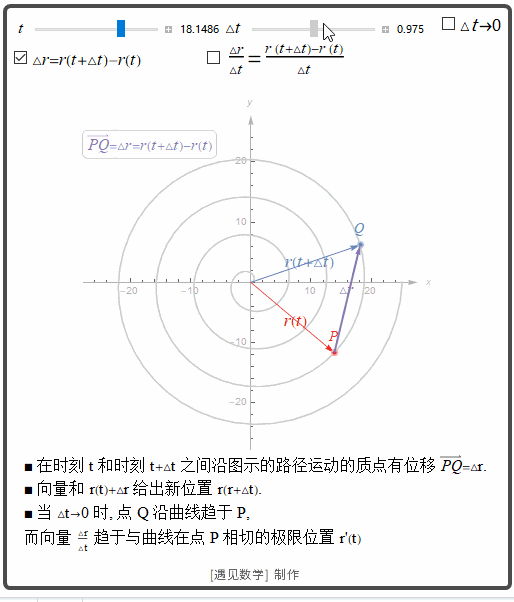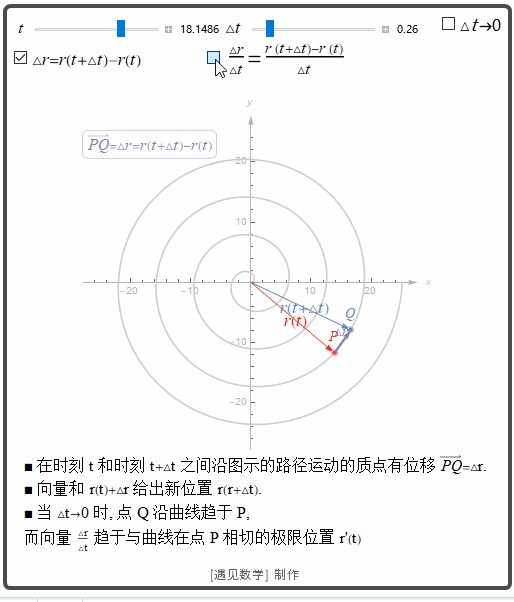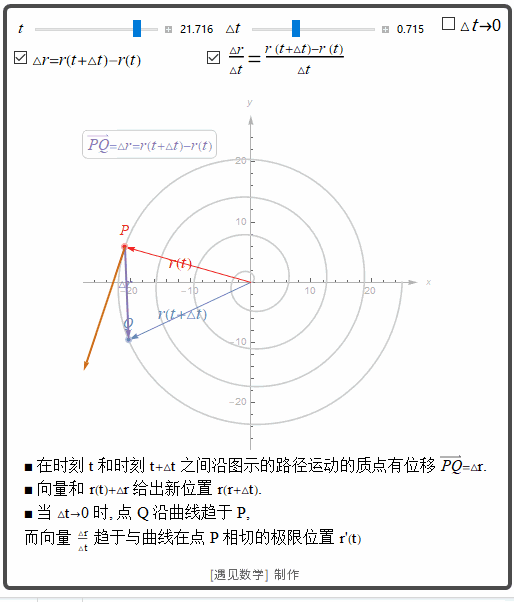
观察下图

导数

从上面动图可以看到, 当 $△\text{t}$ 趋于 0 时, 有三件事情同时发生:首先, Q 沿着曲线趋于 P:割线 PQ 看来趋于点 P 与曲线相切的位置;$\frac{△\text{r}}{△\text{t}}$趋于极限;

如果 dr/dt 是连续且从不为 0 , 则 r 描绘的曲线是光滑的.

因为向量函数的导数是按分量逐个计算的, 对可微向量函数的求导法则对标量函数的求导法则有同样的形式.

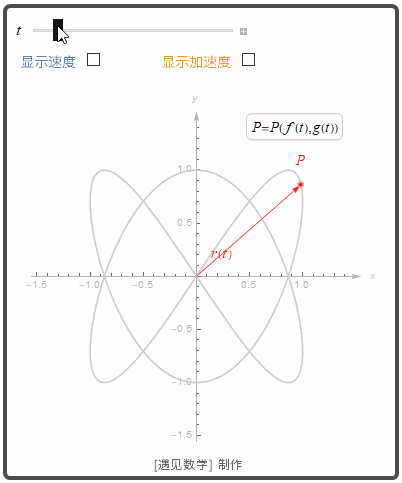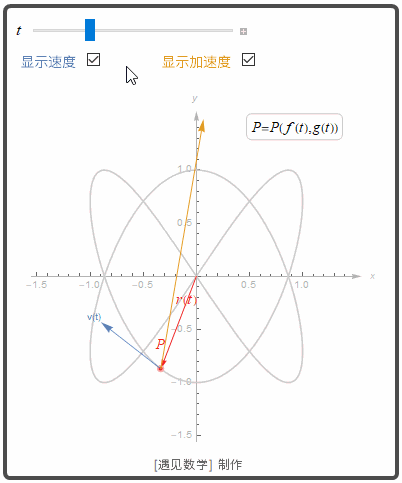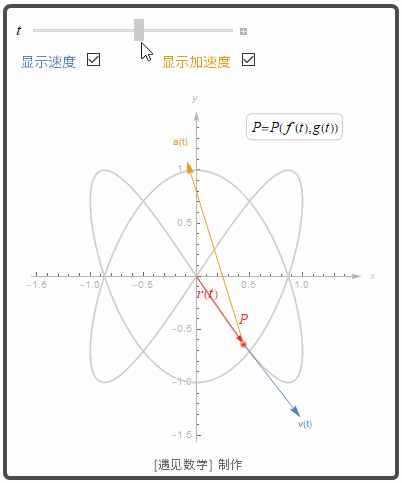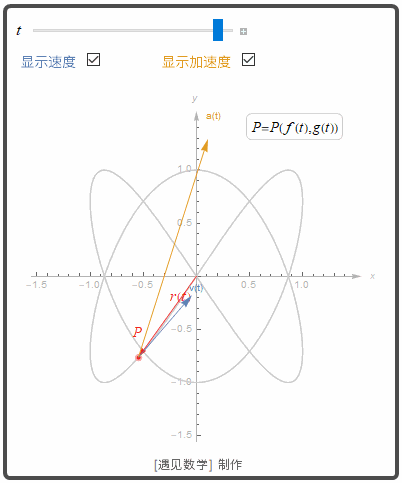
运动

再观察下面的图形

不定积分

r 对 t 的不定积分是 r 的所有反导数的集合. 用 ∫r(t)dt 表示, 若 R 是 r 的任一反导数, 则

定积分

如果 r(t)=f(t)i+g(t)j 的分量在 $\text{[a,b]}$ 上是可积的, 则 r 也如此, 并且从 a 到 b 的 r 的定积分是

(完)

「予人玫瑰, 手留余香」

转发既是支持, 我们会努力走得更远!