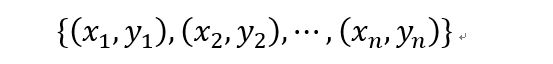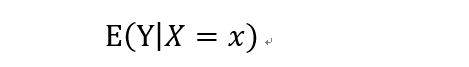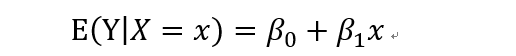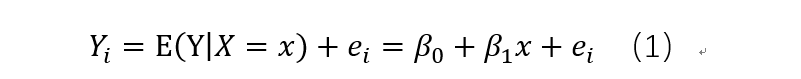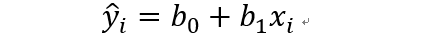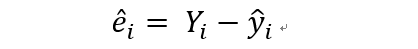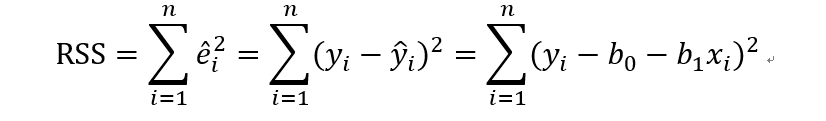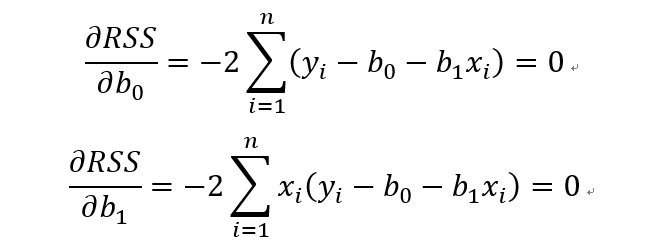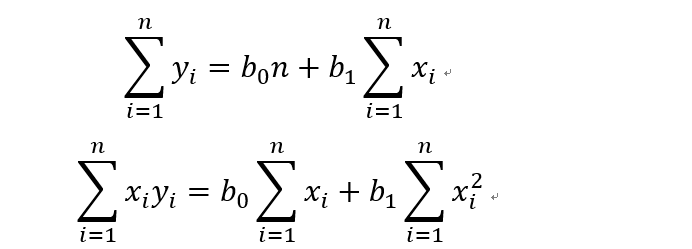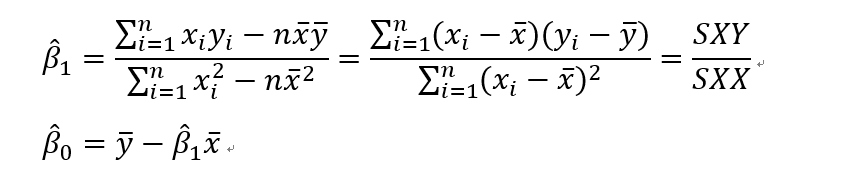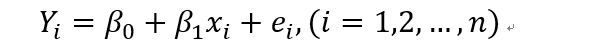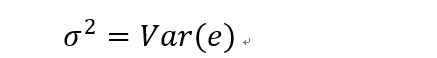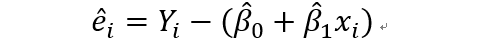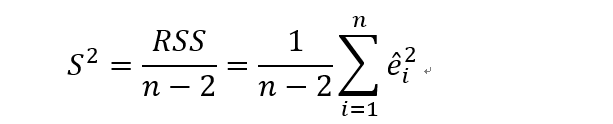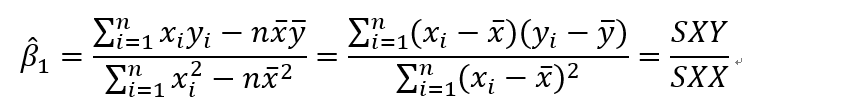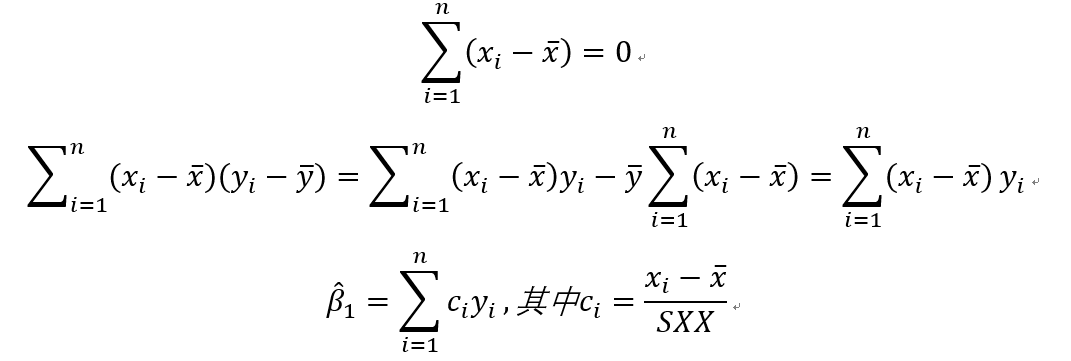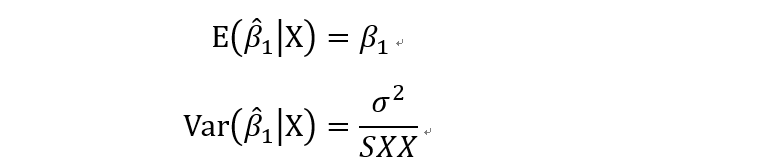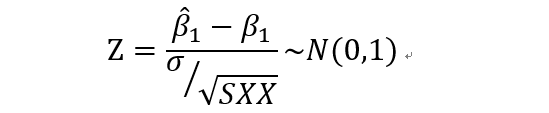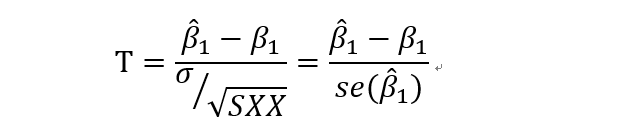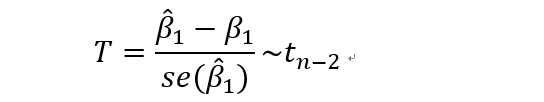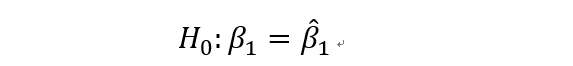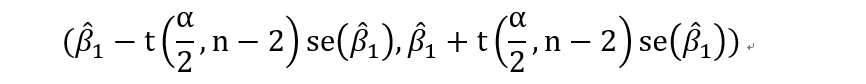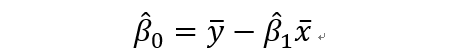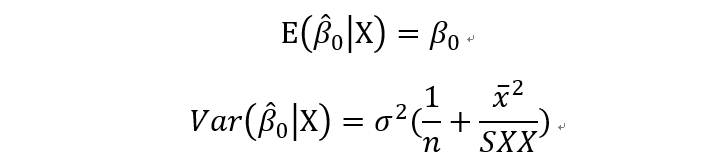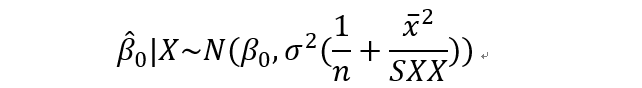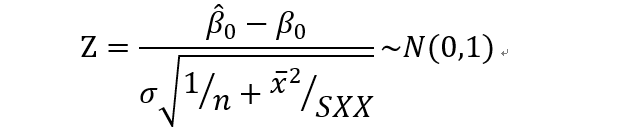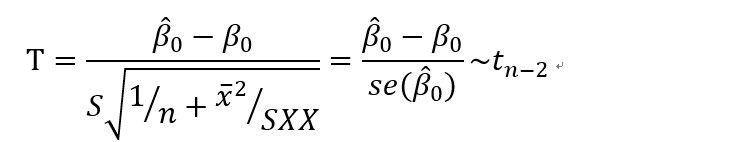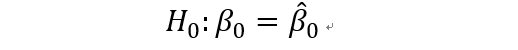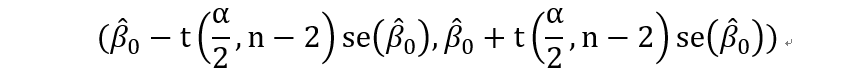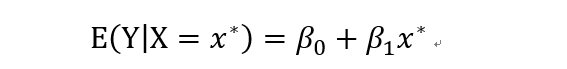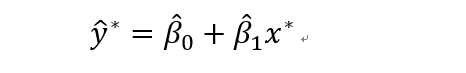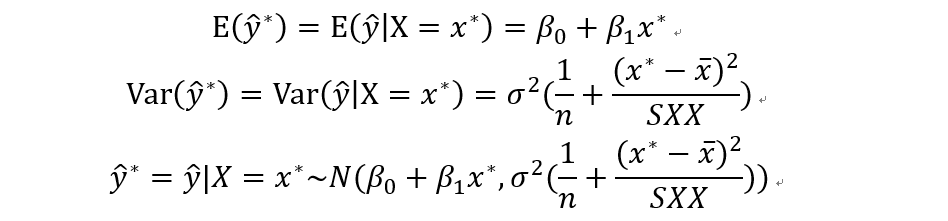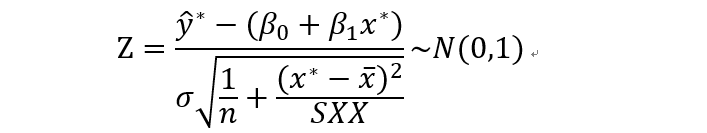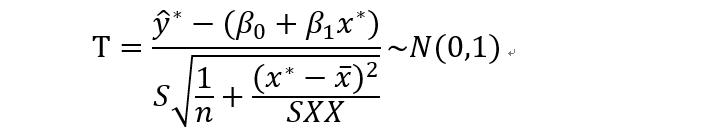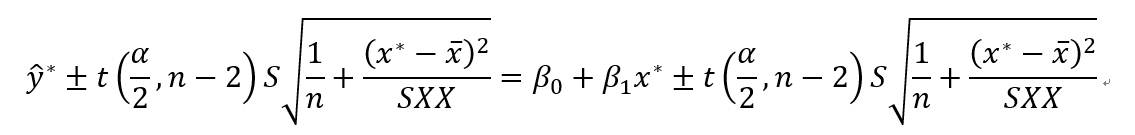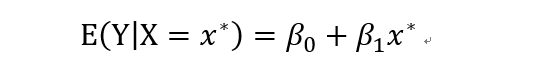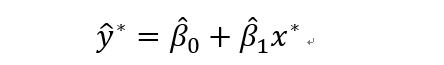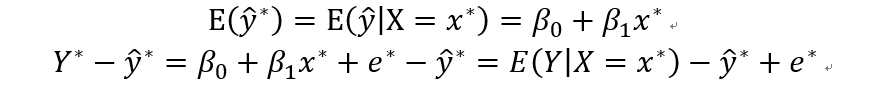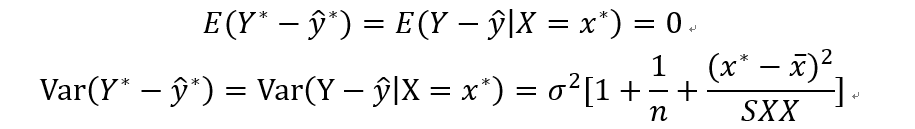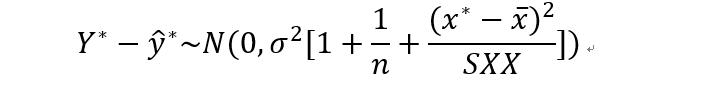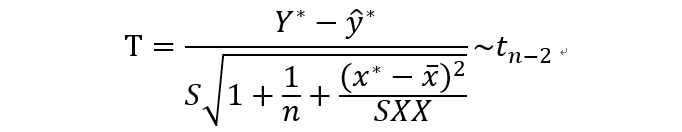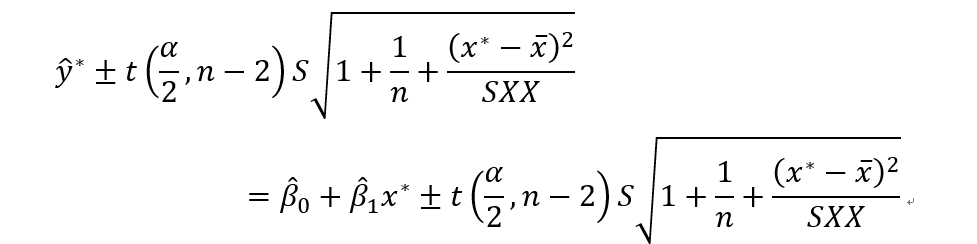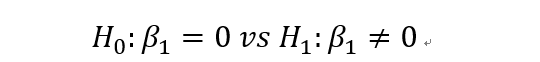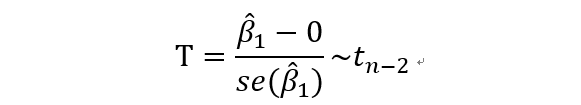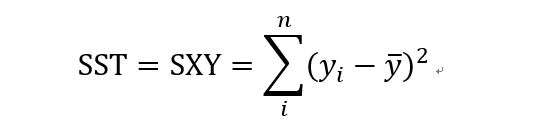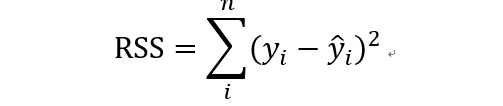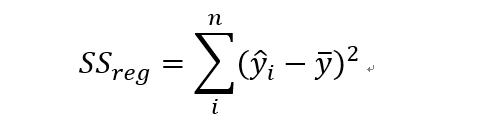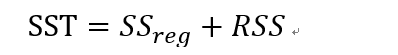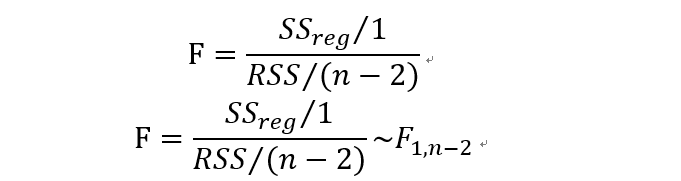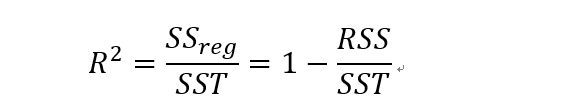[有意思的数学] 一元线性回归

回归分析是机器学习中非常重要的一个模型，常见的回归模型比如一元线性回归，多元线性回归，逻辑回归，非线性回归，岭回归，Lasso回归，支持向量回归等等，而一元线性回归是其他类型的回归分析的基础，所以掌握了一元回归分析的思想，其他的就好理解了。从数学的角度讲，一元回归分析的目的是为了找到两组变量之间的关系。对于回归分析来说，首先需要确定的是回归方程的系数，然后需要对回归方程做假设检验，做这个的目的是为了确定回归关系是否成立，因变量和自变量是否确实存在关系，是否具有统计意义。对回归方程的显著性检验，可以确定全部自变量的总体回归效果。还有一个是对回归系数的检验，回归方程显著，并不能说明每一个自变量都对因变量有影响，而回归系数的检验，可以确定某一个自变量是否对因变量的值有影响，及影响是否显著。但是对于一元线性回归分析来说，回归方程的检验等价于回归系数的检验，因为只有1个因变量，他们的区别体现在多元线性回归分析中。

对于一个确定的了回归方程，我们可以用来做什么？对，可以用来做预测，根据自变量和因变量的历史数据，就可以根据自变量的值推测因变量未来的值，所以我们也要知道，怎么利用回归方程来做预测。还有一个问题是，回归方程是否具有唯一性？参数估计量的置信区间和预测值的置信区间。

下面按照这个思想，看一下每一步具体怎么实现。

 

虽然数学很有意思，但是今天可能不是很有意思。（哭脸）公式有点多，请多一点耐心！

# 回归模型的建立

对于样本数据

其中x叫做自变量或者预测变量，y叫做因变量或者响应变量。

对于简单的线性回归来说，回归分析的目标是当自变量量取确定的值x时，求因变量的期望值：

计算Y的期望值的模型就是我们说的线性回归方程，即：

其中beta0表示直线的截距，beta1表示直线的斜率。

而因变量的实际值为：

其中ei表示随机误差，且期望为0.为什么会有随机误差项呢，它表示因变量中那些不能被自变量解释的部分，也就是所有不能被X解释的因素就是随机误差。对于误差来说，一般有系统误差和随机误差，系统误差是由某种固定的因素造成的，在同样的条件下，系统误差是一直会出现的，而随机误差是由偶然性因素造成的，具有统计意义的分布规律。 

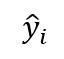
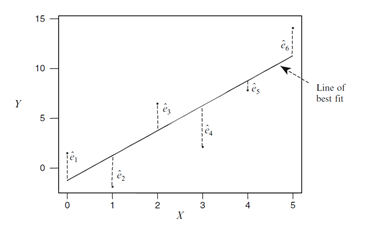
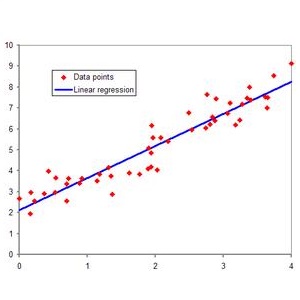
对于线性模型（1）式来说，beta0，beta1是两个未知参数，线性回归的求解过程就是根据样本数据，计算出这两个参数，这里假设估计出的参数分别为b0和b1。称为预测值或者叫拟合值。

我们把真实值和预测值的差，叫做残差。做回归的目标是希望残差越小越好。注意这里一般要求残差是独立的，且具有0均值，同方差的性质，如果残差的均值不一样，就是异方差了。下面这个图1可表示残差的计算。为了求出beta0，beta1两个未知参数，一般的方法就是最小二乘估计，最小二乘的意思是使得全部样本数据的残差的平方和达到最小，平方和最小时，他们的差也达到最小。这样得到的拟合直线就是最优的直线。

图1 残差示意图

假设我们有n个样本点，那么全部样本的残差平方叫做残差平方和，公式

RSS中有2个未知参数b0和b1，为了求RSS的最小值，根据多元函数求极值的方法，分别对b0和b1求偏导数，并令导数为0.

把这两个式子简单做个移项，就可以得到下面这两个式子，一般把这两个式子叫做规范化方程（normal equations）

然后求解这个方程就可以得到

到这里，一元线性回归的模型我们就建立完成了，模型的两个参数求解完毕，beta1尖和beta0尖分别叫做beta1和beta0的估计值。然后我们看一个栗子，如何用R语言实现线性回归。(需要数据的话可以和我联系)

> data <- read.csv("playbill.csv")

> head(data)

> linear <- lm(data$CurrentWeek~data$LastWeek)

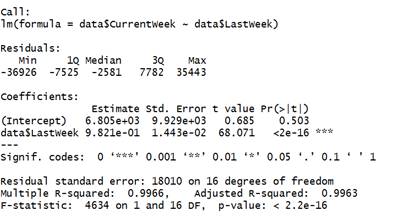
> summary(linear) 

这是R做线性回归的输出结果，首先Call表示回归的自变量和因变量。然后是残差的五数概括。然后是系数估计值，Intercept表示截距，第二行表示beta1的估计值，标准误差，t值，p值。然后三个***表示在检验水平为0.001下显著。下面是自由度以及R^2和调整的R^2，最后一行是模型的F检验值，以及对应的P值。

 

# 回归方程随机项的方差的无偏估计

对于回归方程：

随机误差项具有0均值，同方差的性质。现在要做的是估计方差的值是多少，

对于beta0和beta1的估计值，beta0尖个beta1尖，误差的值可以表示为：

无偏估计为：

这里有个证明，有空可以去看看。

# 回归直线斜率beta的置信区间

前面我们根据最小二乘方法计算出beta1的值：

其中

所以在已知自变量的条件下，根据无偏性，beta1的估计值的期望和方差分别为

即，beta1的估计值服从

 

的正态分布。然后将上式化为标准正态分布, 减去均值除以标准差：

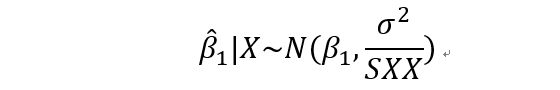
到这里，如果总体方差已知，则使用Z来检验假设，如果总体方差未知，则使用样本方差代替总体方差。

 

使用t检验。其中se（*）表示的是标准误差（standard error，se）

 

回想一下t分布的定义，可以知道这里是服从自由度为n-2的t分布的。自由度的计算公式是样本个数减去带估计参数的个数。

对于假设检验：

beta1的置信区间为：

 

# 直线截距beta0的置信区间

其中beta0的期望和方差为：

所以beta0服从

检验统计量

如果方差未知，则用样本标准差代替总体方差。

对于假设检验：

得到beta0的置信区间为：

# 回归直线的置信区间

对于回归分析得到的回归方程，我们可以做两件事情，一个是对于给定的自变量的值，估计因变量的值；另一个问题是估计因变量的区间。估计值来说，相对比较简单，将自变量的值带进回归方程算一下就ok了。下面看一下怎么求置信区间。

对于确定的自变量的值，带入回归直线中可以得到，

等价于

 

然后用样本方差代替总体方差

就得到了y的置信区间：

 

# 预测区间

刚才说的是置信区间，预测区间和置信区间的区别是什么呢，一般来说，置信区间是对于回归方程中的某个参数来说的，而预测区间是对于给定一个自变量的值，对于因变量的值的预测。这是最主要的区别，别搞混了。

对于给定自变量x*，预测值记做y*。

等价于

期望：

残差的期望和方差为：

分布就是：

统计量：

可得Y的预测区间为：

 

# 回归系数的t检验和回归方程的F检验

对于系数beta1，做假设检验

为了做这个检验，我们选择检验统计量T，

再看一下，总平方和

残差平方和：

回归平方和：

如果对于每个样本i来说，如果预测值和平均值很接近的话，回归平方和趋于0.

总平方和=回归平方和+残差平方和

对于回归方程的显著性检验，可以用F检验。

F服从自由度为（1，n-2）的F分布。在检验水平为alpha时，如果F大于F（1，n-2），那么就拒绝原假设，说明回归方程是显著的。另外一个衡量回归方程显著性的是R方也叫拟合优度，判定系数，可决系数，都是一个意思，R方越大，表明回归方程越显著。

调整的R方：

一元线性回归就先到这里了，不知道大家理解了没有，感觉讲的不太好。（哭）

=============end=============