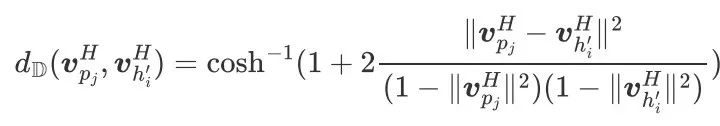赛尔原创@EMNLP 2021 | 利用神经自然逻辑推理进行知识问答

2022 年 3 月 17 日 哈工大SCIR

论文名称： Neural Natural Logic Inference for Interpretable Question Answering

论文作者：石继豪，丁效，杜理，刘挺，秦兵

原创作者：石继豪

论文链接： https://aclanthology.org/2021.emnlp-main.298.pdf

转载须标注出处：哈工大 S C I R

1.概述

本文提出了一种神经符号的方法，该方法在深度学习架构中融入了自然逻辑推理，以搭建准确率高且可解释的问答模型。相比于一阶逻辑，自然逻辑直接在自然语言上进行推理，无需进行一阶逻辑转换，避免了转换过程中的语义损失。所提出的模型按照自然逻辑推理的形式逐步建立假设和前提之间的关联，进而形成了一条证明路径。通过计算假设和前提之间的蕴含分数，来衡量前提蕴含假设的程度。由于自然逻辑推理过程形成了一个树状的分层结构，本文将假设和前提的向量表示投影到双曲空间，以获得更精确的表示。该方法在两个公开的多项选择问答数据集上取得了最好的结果。同时，自然逻辑推理过程固有的性质能够帮助解释推理过程。

2.简介

知识问答是自然语言处理领域在现实场景中很重要的应用，同时也是一项充满挑战的任务，被用来评估人工智能系统理解人类语言进行文本推理的能力。其主要挑战在于答案往往并不会直接存在于知识库中，而是需要系统能够通过从已有的知识库中通过推理的方式得出答案。Angeli等人[1]将知识问答转化为文本蕴含任务，将知识库视为一个由大量前提构成的集合。问题与每个候选答案通过规则的方式转换成陈述句，这些陈述句被视为假设。由此，多项选择知识问答的目的转化为利用大量前提构成的集合找出最可能的假设。神经网络模型已经成为解决知识问答任务的主流模型。然而，多数神经网络模型无法对其推理结果给出解释。因此，构建准确率高同时又具备可解释性的问答系统逐渐引起人们的重视。

所以，本文提出了一个神经符号方法（NeuNLI）用于知识问答，该方法通过将自然逻辑推理[2-3]与深度学习的框架相结合，目的是使整个推理过程遵循自然逻辑的范式，同时与神经网络的结合，使整个系统更加的鲁棒。相比于利用抽象的逻辑形式进行推理（例如利用一阶逻辑进行推理，如何获得抽象的逻辑表示面临很大的挑战），自然逻辑提供了一个基于单调性计算的形式化证明框架。

NeuNLI的核心思想是通过遵循自然逻辑的推理步骤以及借助神经网络模型来将假设与前提建立连接，形成一条证明路径。NeuNLI首先将问题和候选答案转换为陈述句，即假设。然后，通过改写这些假设得到新的假设，并重复这一过程，从而为每个问题-答案对构建一个证明树。由于推理过程是一个树状的分层结构并且自然语言文本在各方面都表现出层次结构，而模型在欧式空间中学习假设和前提的向量表示时，会造成结构失真，所以，NeuNLI将问题和答案的向量表示投射到双曲空间。针对每一棵证明树，NeuNLI在双曲空间中计算树节点和前提之间的蕴含分数，并利用该分数来帮助选择答案。为了以端到端可微的方式训练上述过程，本研究点利用可以有效近似离散变量的Gumbel-Softmax技术作为选择候选改写的近似。

3. 背景

自然逻辑[2]是一种建立在人类语言语法上的形式化证明理论，可以追溯到亚里士多德的三段论。它的目的是通过直接改写语言的结构来进行逻辑推论。逻辑推论通过单调性或投影直接操作在形式化的人类语言[3]，而不是在形如一阶逻辑的抽象逻辑形式上进行推理，因为对于自然语言来说，获得其抽象逻辑形式面临着许多挑战。在该研究点中，提出的神经符号方法不仅能深入了解模型的推导过程，还能避开将人类语言转化为一阶逻辑遇到的困难。

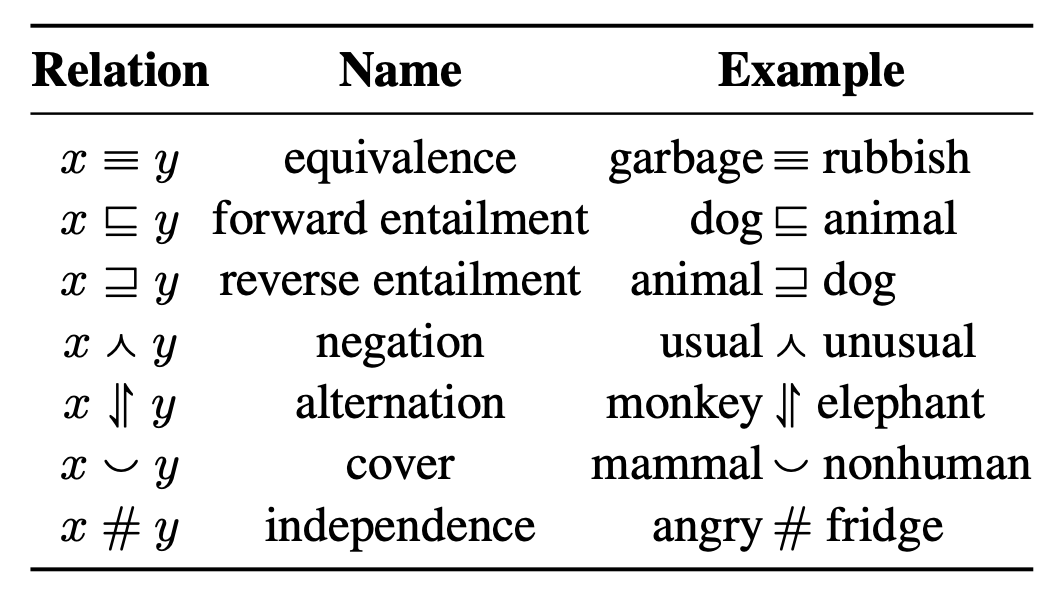
表1 自然逻辑中的七种逻辑关系

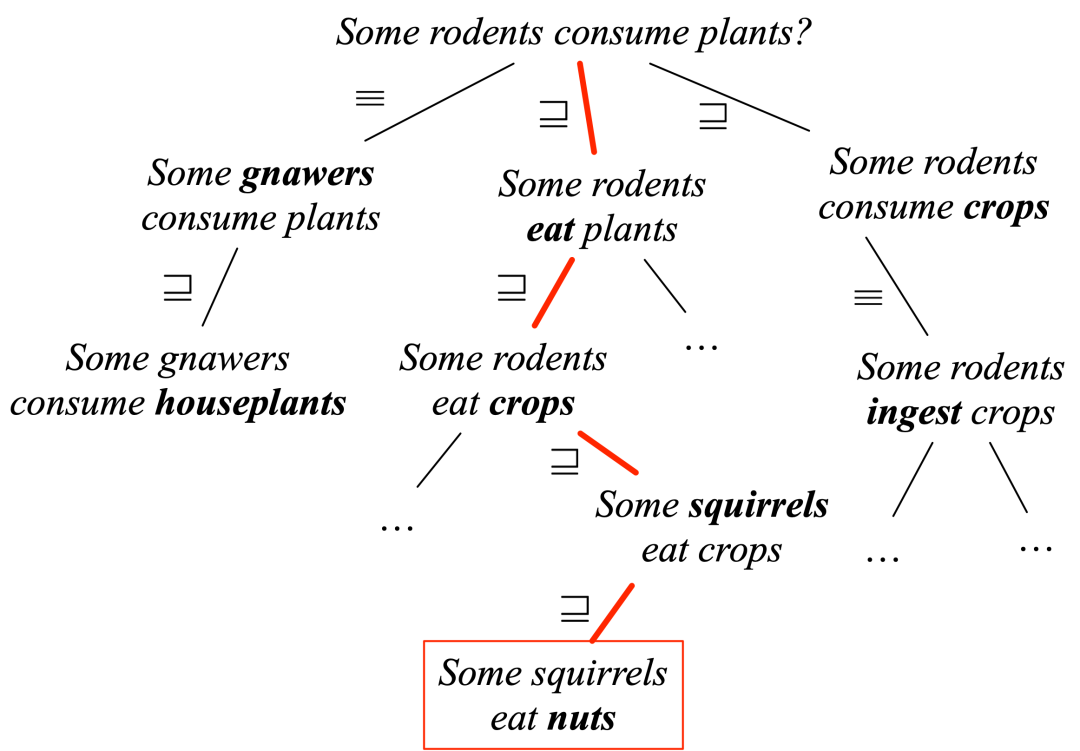
自然逻辑证明的过程是根据单调性或投影原理进行插入、删除或替换词语。MacCartney[3]在其工作中利用了七种逻辑关系，如表1所示。例如，将“animal”替换为“dog”对应于一个反向蕴含关系，即“animal” “dog”。然后，自然逻辑根据上下文确定的单调性来投影单词关系。根据自然逻辑的单调性原理，向上的单调性不更改单词之间的逻辑关系，而向下的单调性可以改变逻辑关系。例如，量词“all”其第一个参数具有向下的单调性。因此，给定“animals” “dogs”,可以很容易推断出“all animals” “all dogs”（例如，“all animals need water” “all dogs need water”）。自然逻辑推理将推理视为一个搜索问题。给定一个假设和一个文本语料库，通过在单词替换（eat consume）的搜索空间进行搜索，直到找到一个前提[4]。整个推理过程从假设开始，逆向寻找前提。图1中给出了一个使用自然逻辑推理的搜索实例。根节点表示本文任务中的一个假设，边上的关系表示句子之间的关系。

图1 自然逻辑证明过程,该过程从一个假设“some rodents consume plants”开始，推理找到了一个前提“some squirrels eat nuts”,边上的标签展示了相连的两个句子之间的逻辑关系

4. 方法

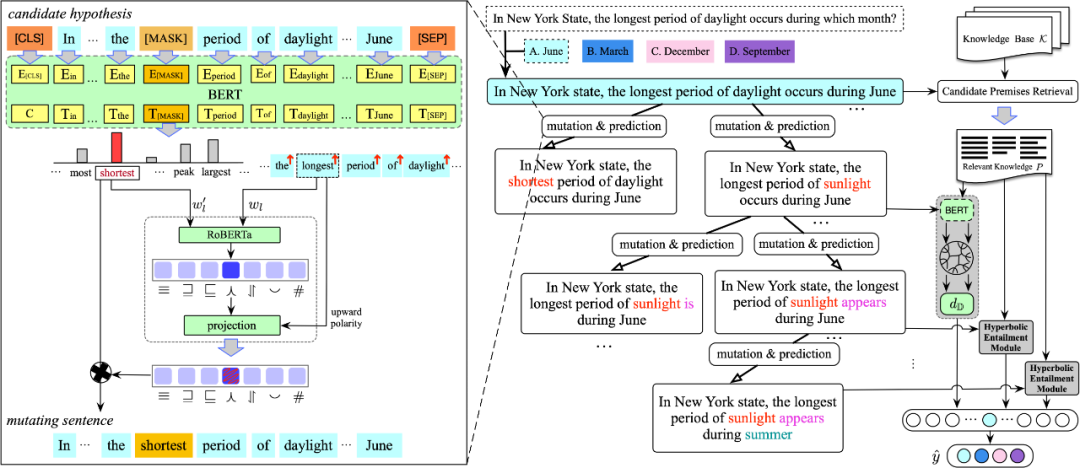
图2 神经自然逻辑推理框架NeuNLI

图2描述了NeuNLI的整体架构。给定一个问题“In New York State, the longest period of daylight occurs during which month”以及候选答案，NeuNLI将问题和每个候选答案（例如“June”）转换为陈述句，即“In New York state, the longest period of daylight occurs during June”。

知识库由非结构化文本组成，使得大量的文本可以作为知识库的来源进行问答。如图2右侧所示，给出一个假设，NeuNLI首先检索候选前提，前提是来自知识库中的一个句子。给定一个假设，通过计算其平均Glove词嵌入分别得到和中每个的表示。然后，分别计算和中的每个之间的余弦相似度，找出前个相关的候选前提。

如图2所示，从根节点的假设开始，通过生成的证明路径从候选前提库中找到能够支撑假设的前提。这些路径是通过新得到的中间假设连接而成，而且遵循自然逻辑推理步骤并采用神经网络的方式获得假设。根据自然逻辑推理步骤，中间的假设总是能够蕴含得到最原始的假设，如果能找到一个蕴含中间假设的前提，那么该前提也能证明原始假设。首先利用掩码遮盖原始假设中的一个词，并将修改后的原始假设送入预训练模型BERT对被遮盖的词进行预测，如图2的左上角所示。为了缩短假设与前提之间的语义距离，逆向搜索还包括单词的插入和删除。例如，“some grey squirrels eat nuts”能够蕴含“some squirrels eat nuts”通过在逆向搜索过程中进行单词的插入。掩码机制并不能保证替换后的假设与替换前的假设语义的一致性，如图2中左面的推理所示。原始假设是“ the longest period of daylight ”，通过对“longest”进行单词替换，候选词中可能包含单词“shortest”，尽管候选词很符合句子的语法规则并且满足单词所处的上下文，但改变了原始假设的语义。为了保证替换前后的语义最大程度的接近，模型利用逻辑关系预测模块判断替换后的句子是否改变替换前的语义，并过滤掉不符合的替换。拿图中的示例举例，候选词是“shortest”，被替换词是“longest”。首先，模型利用精调的RoBERTa预测“shortest”和“longest”之间的逻辑关系。预测的逻辑关系结果是否定关系( )。模型根据预测得到的逻辑关系以及单词的极性利用投影函数判断句子级的语义关系。如果词的极性是单调向上的，那么句子级的关系将与词级别的关系一致。否则，从词级别的关系到句子级的关系，其映射关系如表2。

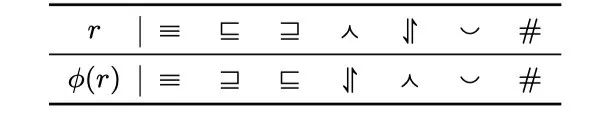
表2 当被替换词的词性是单调向下的时候，投射函数的映射关系。r是单词级别的逻辑关系

由于被替换词“longest”的极性是单调向上的，并且模型预测“longest”和“shortest”之间的逻辑关系是，所以替换前的和替换后的，他们之间的语义关系仍然是，如果分析器给出“longest”的极性是单调向下的，那么句子级关系将会是。由于模型只对或这两种句子级的关系进行推理，所以，用“shortest”进行替换的路径将被剪枝掉。给定一个中间假设，模型需要计算中间假设和每个候选前提之间的蕴含分数。中间假设和候选前提在欧式空间中的向量表示利用BERT预训练模型计算，其输入形式为[CLS] [SEP] [SEP]。标记[CLS]和居中的标记[SEP]的向量表示分别作为候选前提和中间假设的向量表示，符号记作和。对于推理过程形成的树状分层结构，产生的中间假设的数量呈指数级增长。然而，欧氏空间是以多项式的速度增长，这将导致在欧氏空间中学习树状结构的表示会产生结构失真。此外，自然语言文本本身也具有层次结构。因此，模型在双曲空间中计算它们之间的蕴含分数，如图2的右侧部分所示。模型利用Poincare球模型，将候选前提和中间假设投射到双曲空间，以获得更精确的表示和。双曲空间中的蕴含分数是根据双曲距离计算得到，双曲距离的计算公式如下：

模型利用一个可学习的分类器将投影到一个标量值代表蕴含分数。最大的蕴含分数取值用来表示原始假设的蕴含得分，即正确答案的可能性。对于所有的候选答案重复上面的过程，具有最大得分的候选答案被预测为正确答案。

5. 实验

5.1 数据集和基线方法

该研究点在两个公开的数据集[1]上评估模型的性能。这两个数据集由New York Regents 4年级科学考试中的非图表式选择题组成。其中一个数据集（QA-S）由训练集的108个例子、验证集的61个例子和测试集的68个例子组成。另一个数据集（QA-L）规模较大，训练集、验证集和测试集分别有500个例子、249个例子和250个例子。两个外部知识库，一个是Barron学习指南，由1200个句子组成。另一个是Scitext语料库，其中除了包含Barron学习指南，还包含维基百科、字典和科学类教科书，共1,316,278句话。

与实验对比的基线方法有：

Solr是一个信息检索系统，它可以根据问题返回一个置信度分数。给定一个假设，搜索结果中最大的置信度分数被视为该假设的分数。
Classifier[1]是一个基于特征的蕴含分类器，它利用了5个非语义化的实值特征。另外，由Solr信息检索系统得到的置信度分数也可以被看作是一个可选特征。
Evaluation Function是Classifier方法的一个变种。这种方法利用关键词作为特征，而Classifier方法是利用关键短语作为特征。
NaturalLI[1]利用自然逻辑解决问答任务。该方法使用WordNet指导单词的替换过程，而本研究点提出的NeuNLI采用神经网络进行单词替换过程。
HyperQA[5]在双曲空间中学习问题和答案的向量表示。
SemBERT[6]利用显式的上下文语义信息（语义角色标注）对BERT模型进行微调,其在SNLI上表现最好。NeuNLI-E在欧式空间中学习问题和答案的向量表示。

5.3 实验结果

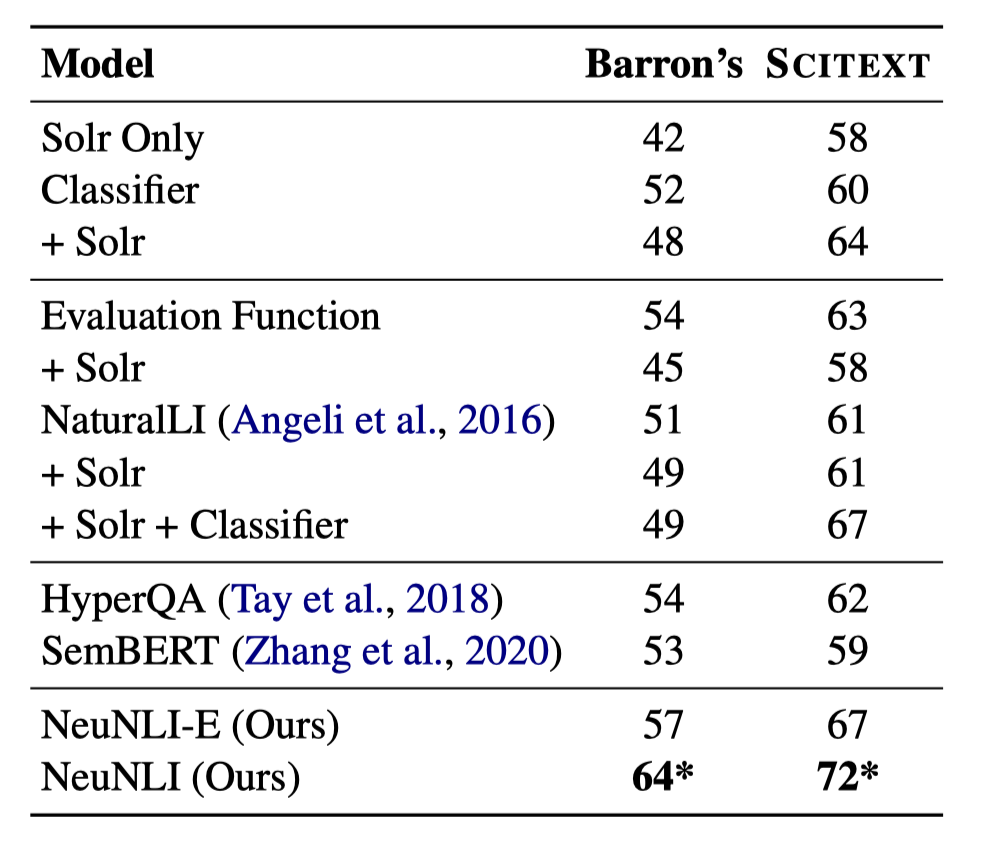
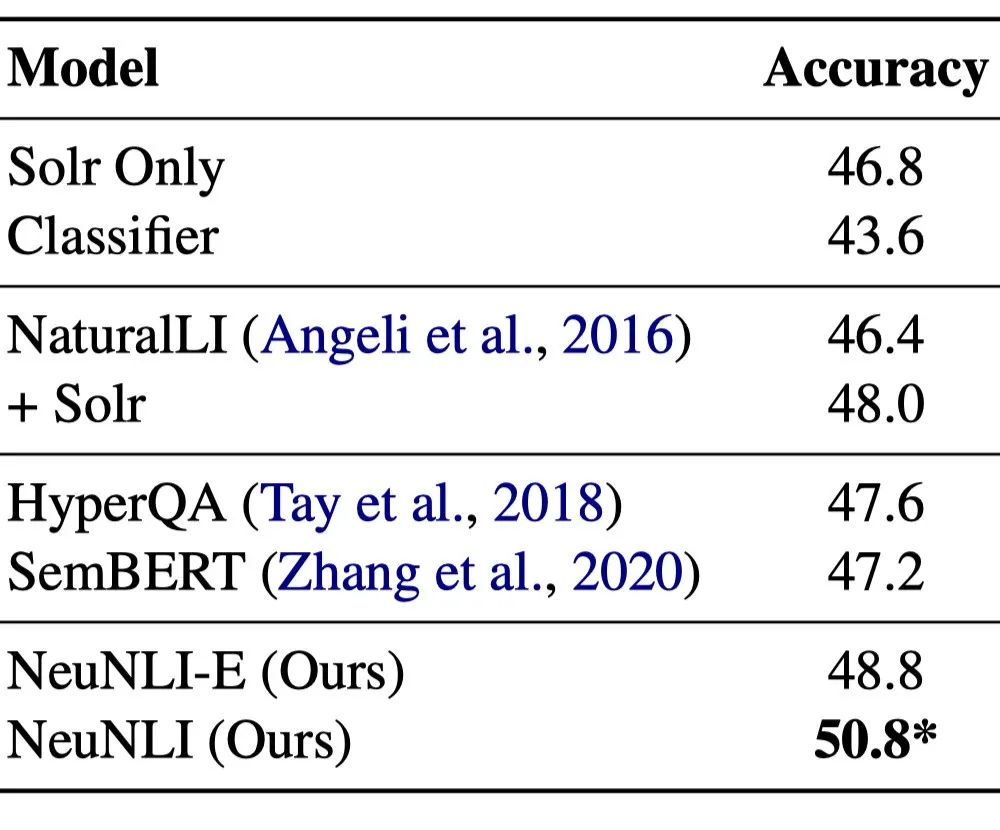
我们在表3（QA-S）和表4（QA-L）中分别列出了基线方法以及NeuNLI在两个测试集上的准确率。在表3中，同时列出利用两个不同知识库的实验结果。

表3 在QA-S数据集上的准确率(%)

表4 在QA-L数据集上的准确率(%)

由实验结果可以发现：

与NaturalLI[1]相比，NeuNLI表现得更好，因为NeuNLI在进行自然逻辑的推理过程中考虑了上下文信息。这有助于减少不必要的无关词语的替换，使NeuNLI专注于正确的推理路径。
HyperQA[5]和NeuNLI进行比较，表明自然逻辑驱动的神经网络可以在QA数据集上取得更好的性能。此外，自然逻辑推理的过程可以作为预测结果的解释，而HyperQA很难对其结果做出合理的解释。
NeuNLI也比SemBERT[6]表现得好。这两种方法都将上下文语义信息与BERT结合起来。相比之下，NeuNLI的方法用到了自然逻辑，这是结果改进的主要原因。
NeuNLI优于NeuNLI-E，主要是因为NeuNLI在双曲空间中学习候选前提和假设的向量表示，使得向量表示更加精确。
NeuNLI在两个不同的知识库上取得了最好的结果。并且，实验发现在更大的知识库Scitext上的模型结果更好，这与人类的直觉吻合，拥有更多的知识，模型可以选择更多的正确答案。
表4中QA-L测试集的实验结果与表3中QA-S测试集的实验结果一致，这说明NeuNLI方法具有普适性。

实验采用人工评价的方式定量地评估了模型的可解释性。评价人员通过对推理路径进行打分（分数取值为{0，1，2}）来评价模型得到的推理路径是否合理。如果最终的中间假设和前提之间的语义毫不相关，分数标记为0；如果两者之间的语义非常接近，分数标记为2；如果两者之间的差距需要评价者脑补一个上下文，分数标记为1。平均得分如表5所示，并且其显著性差异小于0.05。

表5 人工评价结果的平均分数

通过人工评价结果的指标可以看到，NeuNLI的得分明显高于NaturalLI的得分。主要是因为NeuNLI在自然逻辑推理过程中考虑了上下文语义信息，可以生成更合理的词语。例如，假设是“in order to survive, all animals need food, water and air”。利用NeuNLI方法的单词替换，得到句子“in order to live, all animals need food, water and air”，这更接近于“animals need air, water, and food in order to live and thrive”。