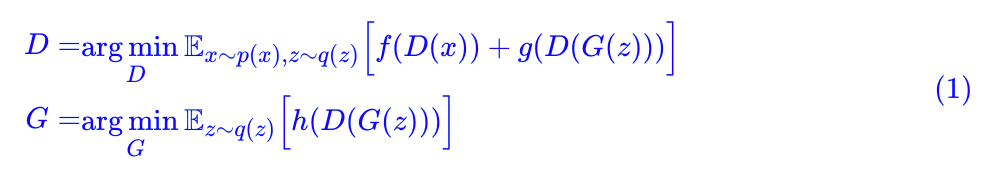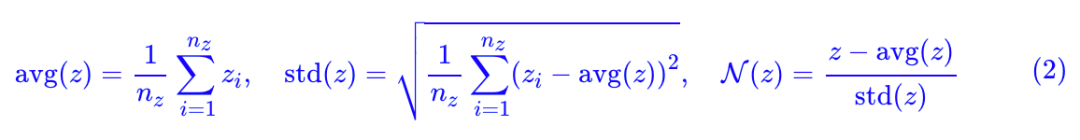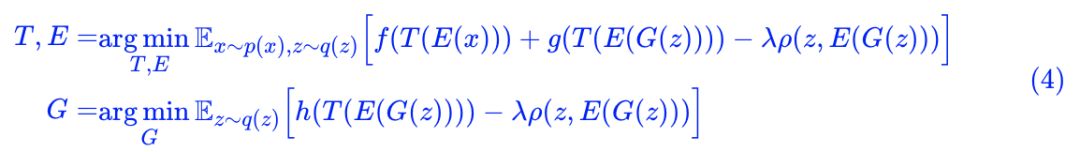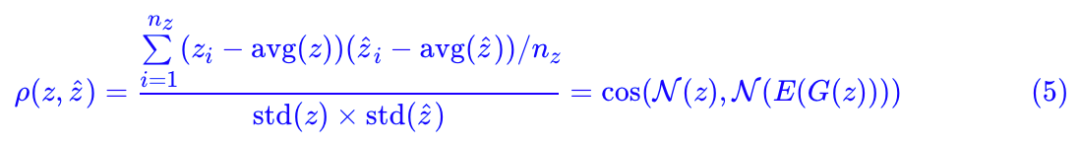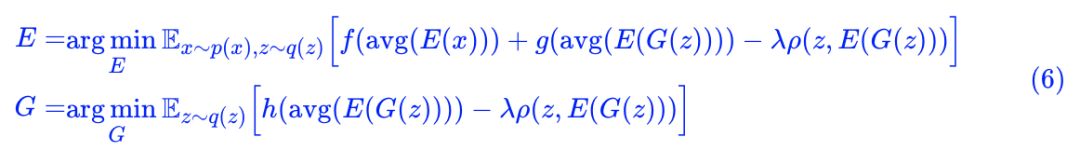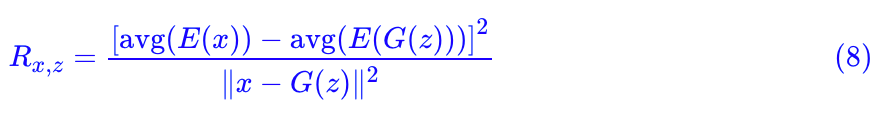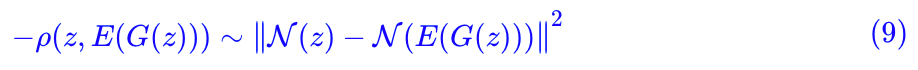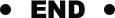会员服务 ·

O-GAN：简单修改，让GAN的判别器变成一个编码器！

2019 年 3 月 8 日 PaperWeekly

作者丨苏剑林

单位丨广州火焰信息科技有限公司

研究方向丨NLP，神经网络

个人主页丨kexue.fm

本文来给大家分享一下笔者最近的一个工作：通过简单地修改原来的 GAN 模型，就可以让判别器变成一个编码器，从而让 GAN 同时具备生成能力和编码能力，并且几乎不会增加训练成本。

这个新模型被称为 O-GAN（正交 GAN，即 Orthogonal Generative Adversarial Network），因为它是基于对判别器的正交分解操作来完成的，是对判别器自由度的最充分利用。

▲ FFHQ线性插值效果图

背景

笔者掉进生成模型的大坑已经很久时间了，不仅写了多篇有关生成模型的文章，而且还往 arXiv 上也提交了好几篇跟生成模型相关的小 paper。自掉坑以来，虽然说对生成模型尤其是 GAN 的理解渐深，有时也觉得自己做出了一点改进工作（所以才提交到 arXiv上），但事实上那些东西都是无关痛痒的修修补补，意义实在不大。

而本文要介绍的这个模型，自认为比以往我做的所有 GAN 相关工作的价值总和还要大：它提供了目前最简单的方案，来训练一个具有编码能力的 GAN 模型。

现如今，GAN 已经越来越成熟，越做越庞大，诸如 BigGAN [1]、StyleGAN [2] 等算是目前最先进的 GAN 模型也已被人熟知，甚至玩得不亦乐乎。不过，这几个最先进的 GAN 模型，目前都只有生成器功能，没有编码器功能，也就是说可以源源不断地生成新图片，却不能对已有的图片提取特征。

当然，带有编码器的 GAN 也有不少研究，甚至本人就曾做过，参考BiGAN-QP：简单清晰的编码 & 生成模型。但不管有没有编码能力，大部分 GAN 都有一个特点：训练完成后，判别器都是没有用的。因为理论上越训练，判别器越退化（比如趋于一个常数）。

做过 GAN 的读者都知道，GAN 的判别器和生成器两个网络的复杂度是相当的（如果还有编码器，那么复杂度也跟它们相当），训练完 GAN 后判别器就不要了，那实在是对判别器这个庞大网络的严重浪费！

一般来说，判别器的架构跟编码器是很相似的，那么一个很自然的想法是能不能让判别器和编码器共享大部分权重？

据笔者所知，过去所有的 GAN 相关的模型中，只有 IntroVAE [3] 做到了这一点。但相对而言 IntroVAE 的做法还是比较复杂的，而且目前网上还没有成功复现 IntroVAE 的开源代码，笔者也尝试复现过，但也失败了。

而本文的方案则极为简单——通过稍微修改原来的GAN模型，就可以让判别器转变为一个编码器，不管是复杂度还是计算量都几乎没有增加。

模型

事不宜迟，马上来介绍这个模型。首先引入一般的 GAN 写法：

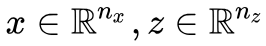
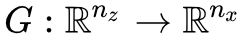
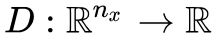
为了不至于混淆，这里还是不厌其烦地对符号做一些说明。其中，p(x) 是真实图片集的“证据分布”，q(z) 是噪声的分布（在本文中，它是元标准正态分布）；而和自然就是生成器和判别器了，f, g, h 则是一些确定的函数，不同的 GAN 对应着不同的 f, h, g。

有时候我们会加一些标准化或者正则化手段上去，比如谱归一化或者梯度惩罚，简单起见，这些手段就不明显地写出来了。

然后定义几个向量算符：

写起来貌似挺高大上的，但其实就是向量各元素的均值、方差，以及标准化的向量。特别指出的是，当 nz≥3 时（真正有价值的 GAN 都满足这个条件），[avg(z),std(z),N(z)] 是函数无关的，也就是说它相当于是原来向量 z 的一个“正交分解”。

接着，我们已经说了判别器的结构其实和编码器有点类似，只不过编码器输出一个向量而判别器输出一个标量罢了，那么我可以把判别器写成复合函数：

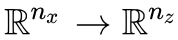
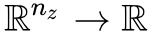
这里 E 是的映射，而 T 是的映射。不难想象，E 的参数量会远远多于 T 的参数量，我们希望 E(x) 具有编码功能。

怎么实现呢？只需要加一个 loss：Pearson 相关系数！

其中：

如果 λ=0，那么就是普通的 GAN 而已（只不过判别器被分解为两部分 E 和 T 两部分）。加上了这个相关系数，直观上来看，就是希望 z 和 E(G(z)) 越线性相关越好。为什么要这样加？我们留到最后讨论。

显然这个相关系数可以嵌入到任意现成的 GAN 中，改动量显然也很小（拆分一下判别器、加一个 loss），笔者也做了多种 GAN 的实验，发现都能成功训练。

这样一来，GAN 的判别器 D 分为了 E 和 T 两部分，E 变成了编码器，也就是说，判别器的大部分参数已经被利用上了。但是还剩下 T，训练完成后 T 也是没用的，虽然 T 的参数量比较少，这个浪费量是很少的，但对于有“洁癖”的人（比如笔者）来说还是很难受的。

能不能把 T 也省掉？经过笔者多次试验，结论是：还真能！因为我们可以直接用 avg(E(x)) 做判别器：

这样一来整个模型中已经没有 T 了，只有纯粹的生成器 G 和编码器 E，整个模型没有丝毫冗余的地方，洁癖患者可以不纠结了。

实验

这样做为什么可以？我们放到最后再说。先看看实验效果，毕竟实验不好的话，原理说得再漂亮也没有意义。

注意，理论上来讲，本文引入的相关系数项并不能提高生成模型的质量，所以实验的目标主要有两个：1）这个额外的 loss 会不会有损原来生成模型的质量；2）这个额外的 loss 是不是真的可以让 E 变成一个有效的编码器？

刚才也说，这个方法可以嵌入到任意 GAN 中，这次实验用的是 GAN 是我之前的 GAN-QP 的变种：

其中：

数据集上，这次的实验做得比较完整，在 CelebA HQ、FFHQ、LSUN-churchoutdoor、LSUN-bedroom 四个数据集上都做了实验，分辨率都是 128 × 128 （其实还做了一点 256 × 256 的实验，结果也不错，但是没放到论文上）。模型架构跟以往一样都是 DCGAN [4]，其余细节直接看论文或者代码吧。

上图：

▲ CelebA HQ随机生成

▲ CelebA HQ重构效果

▲ CelebA HQ线性插值

▲ FFHQ随机生成

▲ FFHQ重构效果

▲ FFHQ线性插值

▲ LSUN-church随机生成

▲ LSUN-church重构效果

▲ LSUN-church线性插值

▲ LSUN-bedroom随机生成

▲ LSUN-bedroom重构效果

▲ LSUN-bedroom线性插值

不管你们觉得好不好，反正我是觉得还好了。

1. 随机生成效果还不错，说明新引入的相关系数项没有降低生成质量；

2. 重构效果还不错，说明 E(x) 确实提取到了 x 的主要特征；

3. 线性插值效果还不错，说明 E(x) 确实学习到了接近线性可分的特征。

原理

好，确认过眼神，哦不对，是效果，就可以来讨论一下原理了。

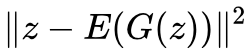
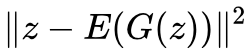
很明显，这个额外的重构项的作用就是让 z 尽可能与 E(G(z)) “相关”，对于它，相信大多数读者的第一想法应该是 mse 损失而非本文用的 ρ(z,E(G(z)))。但事实上，如果加入那么训练基本上都会失败。那为什么 ρ(z,E(G(z))) 又会成功呢？

根据前面的定义，E(x) 输出一个维的向量，但是 T(E(x)) 只输出一个标量，也就是说，E(x) 输出了个自由度，而作为判别器，T(E(x)) 至少要占用一个自由度（当然，理论上它也只需要占用一个自由度）。

如果最小化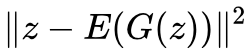，那么训练过程会强迫 E(G(z)) 完全等于 z，也就是说个自由度全部被它占用了，没有多余的自由度给判别器来判别真假了，所以加入大概率都会失败。

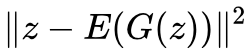
但是 ρ(z,E(G(z))) 不一样，ρ(z,E(G(z))) 跟 avg(E(G(z))) 和 std(E(G(z))) 都没关系（只改变向量 E(G(z)) 的 avg 和 std，不会改变 ρ(z,E(G(z))) 的值，因为 ρ 本身就先减均值除标准差了），这意味着就算我们最大化 ρ(z,E(G(z)))，我们也留了至少两个自由度给判别器。

这也是为什么在 (6) 中我们甚至可以直接用 avg(E(x)) 做判别器，因为它不会被 ρ(z,E(G(z))) 的影响的。

一个相似的例子是 InfoGAN [5]。InfoGAN 也包含了一个重构输入信息的模块，这个模块也和判别器共享大部分权重（编码器），而因为 InfoGAN 事实上只重构部分输入信息，因此重构项也没占满编码器的所有自由度，所以 InfoGAN 那样做是合理的——只要给判别器留下至少一个自由度。

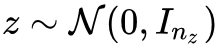
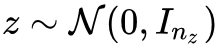
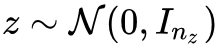
另外还有一个事实也能帮助我们理解。因为我们在对抗训练的时候，噪声是的，当生成器训练好之后，那么理论上对所有的，G(z) 都会是一张逼真的图片，事实上，反过来也是成立的，如果 G(z) 是一张逼真的图片，那么应该有（即位于 N(0,Inz) 的高概率区域）。

进一步推论下去，对于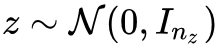，我们有 avg(z)≈0 以及 std(z)≈1。那么，如果 G(z) 是一张逼真的图片，那么必要的条件是 avg(z)≈0 以及 std(z)≈1。

应用这个结论，如果我们希望重构效果好，也就是希望 G(E(x)) 是一张逼真的图片，那么必要的条件是 avg(E(x))≈0 以及 std(E(x))≈1。

这就说明，对于一个好的 E(x)，我们可以认为 avg(E(x)) 和 std(E(x)) 都是已知的（分别等于 0 和 1），既然它们是已知的，我们就没有必要拟合它们，换言之，在重构项中可以把它们排除掉。而事实上：

也就是说在 mse 损失中排除掉 avg(E(x)) 和 std(E(x)) 的话，然后省去常数，它其实就是 −ρ(z,E(G(z)))，这再次说明了 ρ(z,E(G(z))) 的合理性。并且由这个推导，重构过程并不是 G(E(x)) 而是：

最后，这个额外的重构项理论上还能防止 mode collapse 的出现。其实很明显，因为重构质量都不错了，生成质量再差也差不到哪里去，自然就不会怎么 mode collapse 了。

非要说数学依据的话，我们可以将 ρ(z, E(G(z))) 理解为 Z 和 G(Z) 的互信息上界，所以最小化 −ρ(z, E(G(z))) 事实上在最大化 Z 与 G(Z) 的互信息，这又等价于最大化 G(Z) 的熵。而 G(Z) 的熵大了，表明它的多样性增加了，也就远离了 mode collapse。类似的推导可以参考能量视角下的GAN模型（二）：GAN＝“分析”＋“采样”。

结语

本文介绍了一个方案，只需要对原来的 GAN 进行简单的修改，就可以将原来 GAN 的判别器转化为一个有效的编码器。多个实验表明这样的方案是可行的，而对原理的进一步思考得出，这其实就是对原始判别器（编码器）的一种正交分解，并且对正交分解后的自由度的充分利用，所以模型也被称为“正交 GAN（O-GAN）”。

小改动就收获一个编码器，何乐而不为呢？欢迎大家试用。

后记

事后看，本文模型的思想其实本质上就是“直径和方向”的分解，并不难理解，但做到这件事情不是那么轻松的。

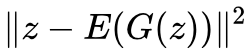
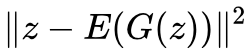
最开始我也一直陷入到的困境中，难以自拔，后来我想了很多技巧，终于在的重构损失下也稳定住了模型（耗了几个月），但模型变得非常丑陋（引入了三重对抗 GAN），于是我着手简化模型。后来我尝试用 cos 值用重构损失，发现居然能够简单地收敛了，于是我思考背后的原理，这可能涉及到自由度的问题。

接着我尝试将 E(x) 分解为模长和方向向量，然后用模长 ||E(x)|| 做判别器，用 cos 做重构损失，判别器的 loss 用 hinge loss。这样做其实几何意义很明显，说起来更漂亮些，部分数据集是 work 的，但是通用性不好（CelebA 还行，LSUN 不行），而且还有一个问题是 ||E(x)|| 非负，无法嵌入到一般的 GAN，很多稳定 GAN 的技巧都不能用。

然后我想怎么把模长变成可正可负，开始想着可以对模长取对数，这样小于 1 的模长取对数后变成负数，大于 1 的模长取对数变成正数，自然达成了目的。但是很遗憾，效果还是不好。后来陆续实验了诸多方案都不成功，最后终于想到可以放弃模长（对应于方差）做判别器的 loss，直接用均值就行了。所以后来转换成 avg(E(x))，这个转变经历了相当长的时间。

还有，重构损失一般认为要度量 x 和 G(E(x)) 的差异，而我发现只需要度量 z 和 E(G(z)) 的差异，这是最低成本的方案，因为重构是需要额外的时间的。最后，我还做过很多实验，很多想法哪怕在 CelebA上都能成功，但LSUN上就不行。所以，最后看上去简单的模型，实际上是艰难的沉淀。

整个模型源于我的一个执念：判别器既然具有编码器的结构，那么就不能被浪费掉。加上有 IntroVAE 的成功案例在先，我相信一定会有更简单的方案实现这一点。前前后后实验了好几个月，跑了上百个模型，直到最近终于算是完整地解决了这个问题。

对了，除了 IntroVAE，对我启发特别大的还有 Deep Infomax [6] 这篇论文，Deep Infomax 最后的附录里边提供了一种新的做 GAN 的思路，我开始也是从那里的方法着手思考新模型的。

参考文献

[1] Andrew Brock, Jeff Donahue, Karen Simonyan, Large Scale GAN Training for High Fidelity Natural Image Synthesis, arXiv:1809.11096.

[2] Tero Karras, Samuli Laine, Timo Aila, A Style-Based Generator Architecture for Generative Adversarial Networks, arXiv:1812.04948.

[3] Huaibo Huang, Zhihang Li, Ran He, Zhenan Sun, Tieniu Tan, ntroVAE: Introspective Variational Autoencoders for Photographic Image Synthesis, NeurIPS 2018.

[4] Alec Radford, Luke Metz, Soumith Chintala, Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks, ICLR 2016.

[5] Xi Chen, Yan Duan, Rein Houthooft, John Schulman, Ilya Sutskever, Pieter Abbeel, InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets, NIPS 2016.

[6] R Devon Hjelm, Alex Fedorov, Samuel Lavoie-Marchildon, Karan Grewal, Phil Bachman, Adam Trischler, Yoshua Bengio, Learning deep representations by mutual information estimation and maximization, ICLR 2019.