ICLR 2023 最高分论文被锤抄袭??

极市导读
究竟是Git Clone还是Git Re-Basin?被评论区长文石锤! >>算法offer直通车、50万总奖池!高通人工智能创新应用大赛等你来战!
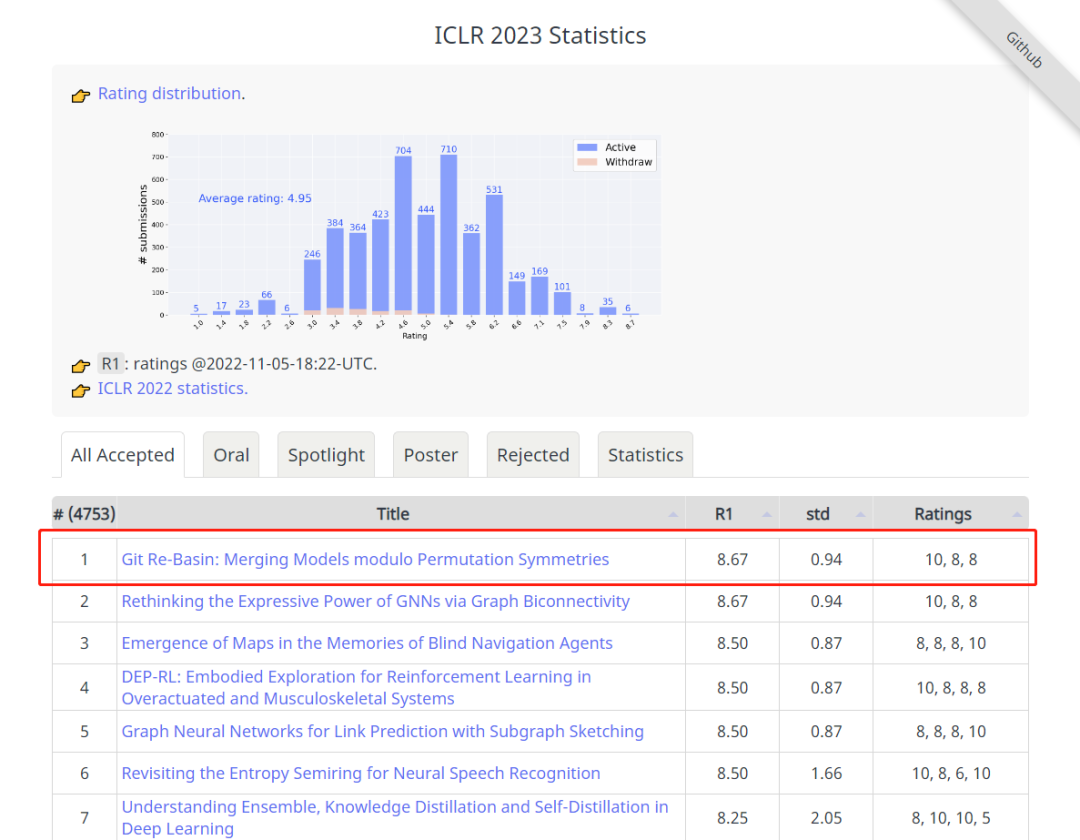
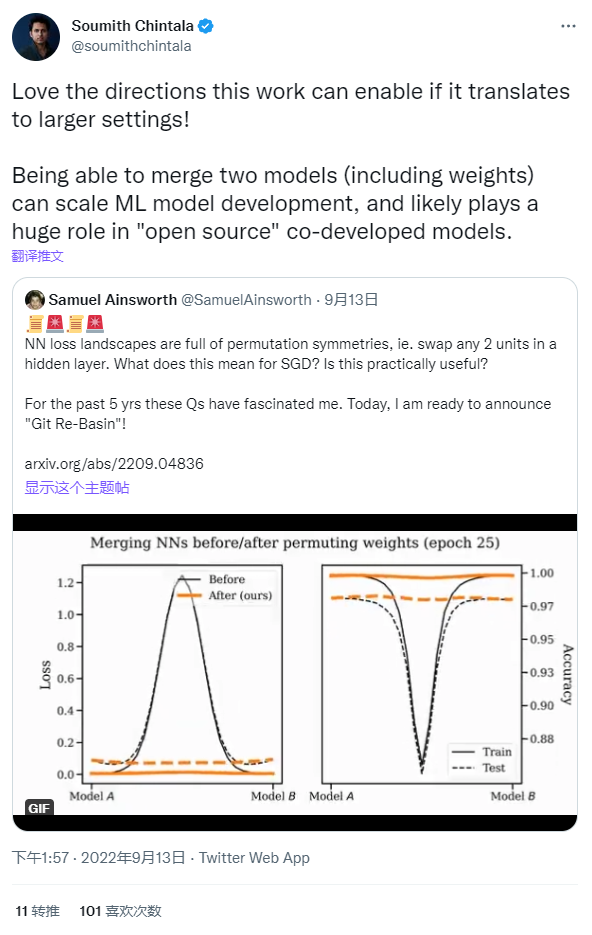
如上图所示,ICLR 2023 官方近期正式宣布评审工作已结束,评分最高的 Git Re-Basin 这项神经网络启发性新研究探索了在深度学习中,SGD算法在高维非凸优化问题令人惊讶的有效性。这篇来自华盛顿大学的工作在推特引起了火热讨论,甚至连 Pytorch 的联合创始人 Soumith Chintala 也发文盛赞,他表示如果这项研究如果转化为更大的设置,实现的方向将会更棒,能够合并包括权重的两个模型,可以扩展 ML 模型开发,并可能在“开源”的联合开发模型中发挥巨大的作用。
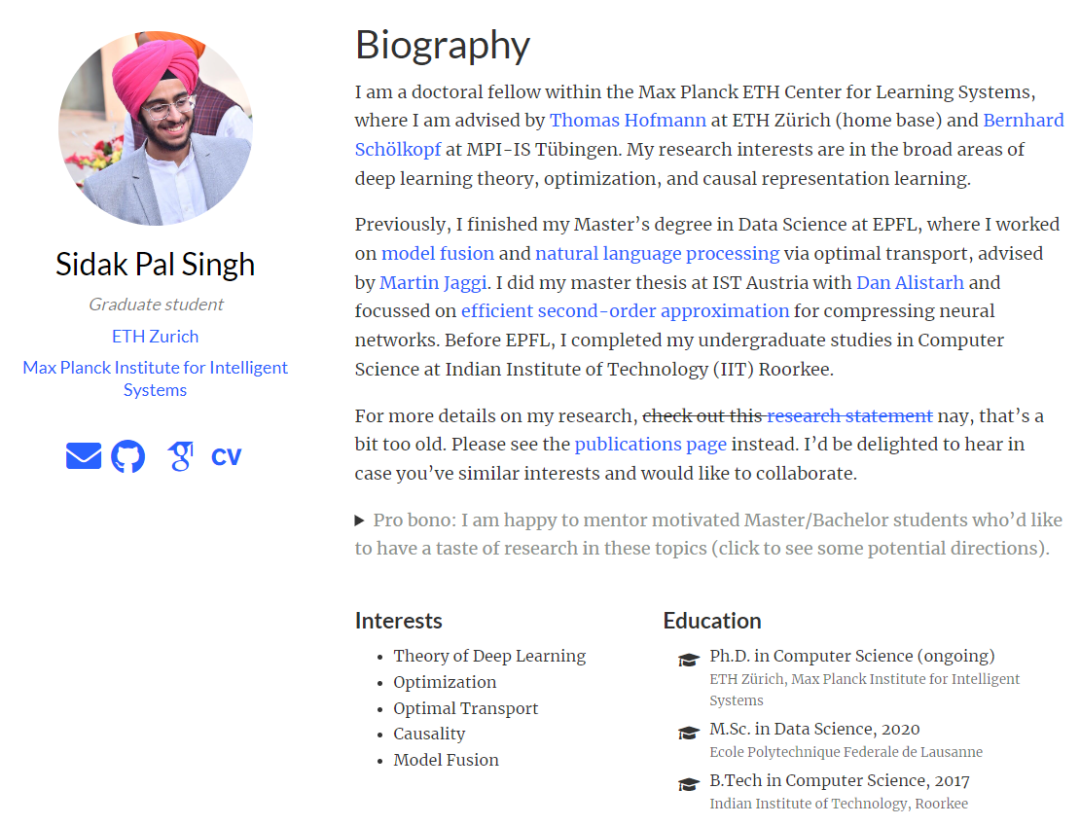
但就在前两天,OpenReview 上竟然有 public comment 发布长文,石锤这篇 ICLR 最高分论文涉嫌抄袭,并且在评论区详细推导了它和之前工作的等价性。这位发表长文评论的作者 Sidak Pal Singh 是深度学习理论、优化和因果表征学习领域的学者,恰好他就比较关注 Optimization 问题,发现了这篇工作的一些端倪,以下将会进行详细的解读。
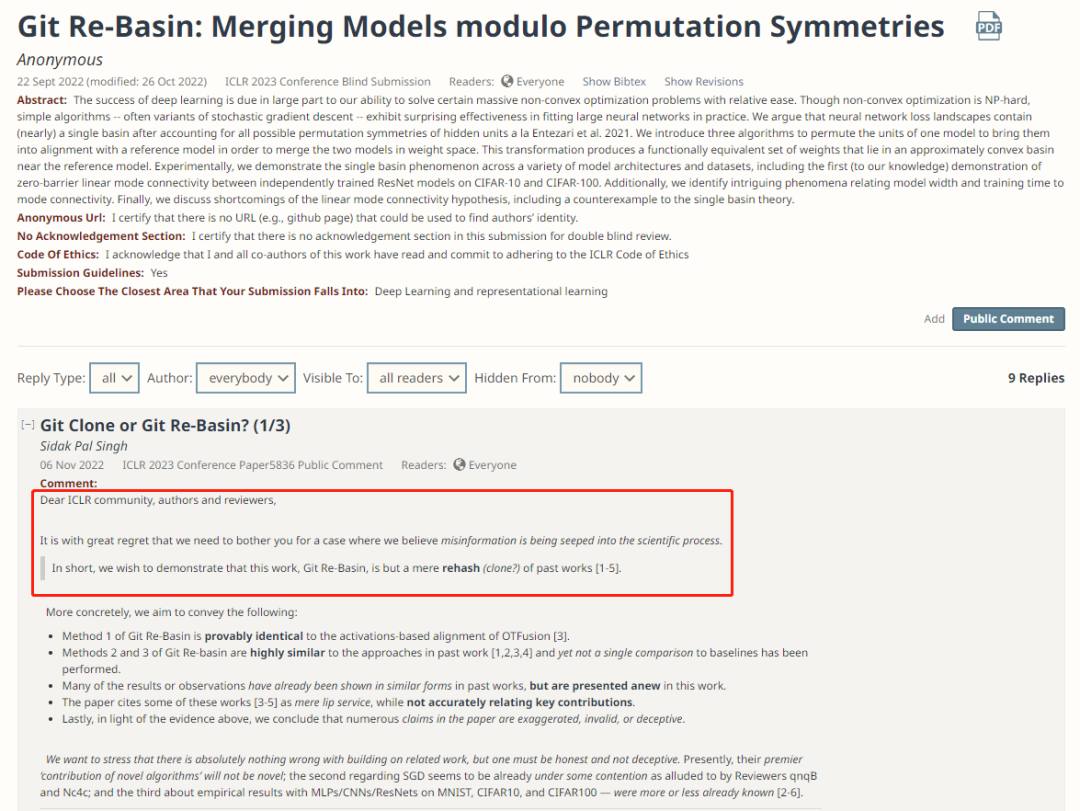
Sidak Pal Singh 的这篇评论从题目就开始质问:究竟是「Git Clone」还是「Git Re-Basin」?开篇更是直截了当地指出这篇工作是将过去的许多工作综合在一起“炒冷饭”:
-
Git Re-Basin 的方法 1 被证明与 OTFusion[3] 的基于激活的对齐方法相同。 -
Git Re-basin 的方法 2 和 3 与过去工作中的方法 [1,2,3,4] 高度相似,但没有进行任何与 Baseline 的比较。 -
许多结果或观察在过去的工作中已经以类似的形式表现出来,但 在本文中被重新呈现了出来。 -
文中引用其中一些著作 [3-5] 只是做做表面工夫,而没有准确地列出其关键贡献。
所以综上所述,Sidak Pal Singh 申斥文中许多主张是夸大、无效乃至欺骗性的。
Sidak Pal Singh 还强调了这是学术不端现象,他指出,在相关工作的基础上做研究是绝对没有错的,但必须诚实、不能欺骗。
-
目前,他们主要的“新算法的贡献”似乎并不新。 -
正如论文审稿人 qnqB 和 Nc4c 所暗示的那样,关于 SGD 的问题似乎已经存在着一些争议; -
MLPs/CNNs/ResNets 在 MNIST、CIFAR10 和 CIFAR100 上的实证结果,这些都或多或少是已知的 [2-6]。
(A) 等价于[3]的数学证明
首先要从数学上证明 Git Re-Basin 的方法 1(基于匹配激活)与 Singh&Jaggi(2019)[3] 中使用的方法之一相同。[3] 的主要思想是利用最优传输(OT)首先获得给定网络的分层对齐,然后在对齐后分别对其参数求平均值。
以下证明的要点是,对于均匀边缘和欧氏度规,由于经典的 Birkhoff-von Neumann 定理,方法 1 和基于 OT 的[3]方法的解集是相同的。(这是相当直接的,可以在推论1 https://mathematical-tours.github.io/book-sources/optimal-transport/CourseOT.pdf 中找到对其他类型代价的更普遍的证明)
概括一下,OT 问题可以表示为如下线性规划:
其中,运输计划
表示从“源位置”移动到“目的位置”的“货物”数量,并且必须满足源和目的地(即
和
)的质量守恒约束。进一步地,将 ground cost 矩阵记为
,其中的元素指定了相应的源-目的地对之间的单位运输成本。
为简单起见,在 [3] 中,假设所有神经元都具有同等的重要性(在上述说法中,“供应”和“需求”的数量相同),因此我们可以设置 。为了方便,我们将传输图 乘以标量 称为 ,即 ,而 现在是一个双随机矩阵(所有行和列的总和必须为1)。
现在,我们考虑 [3] 的基于激活的方法,其中成本矩阵 可以用Git Re-Basin的表示法表示为 。
然后使用简写的 和 提取各自矩阵的对角线(向量),我们可以将代价矩阵表示为:
因此,我们可以将OT问题表示为:
现在,利用质量守恒的约束条件,我们得到了下面的等价问题:
因此,我们认为上述优化目标与本文的公式 1 中的优化目标相同。
似乎还有一个区别:OT 的域是双随机矩阵的集合,而 Git Re-Basin 的域是排列矩阵的集合。但是,任何学过线性规划课程的人都知道,线性规划的解是在多元面(即顶点)的极值点上找到的。由于著名的Birkhoff-von Neumann 定理,Birkhoff polytope(双随机矩阵)的极值点恰恰是置换矩阵,因此这两个问题的解是相同的。
因此,本研究的方法 1 只是 [3] 的一个特例,并且在考虑其基于激活的 ground cost 时与 [3] 相同。
备注:作者指出,作为他们方法 1 的进一步变体,也可以使用激活的互相关矩阵。必须注意的是,这一点在 [5,第6页] 中已经考虑过了。
让我们一起来看看 Git Re-Basin 是怎么说的:

等等,咱们别忽略其他两个算法呀,它们也有类似的命运!

(B) 方法 2 和方法 3 与之前的研究 [1,2,3,4] 高度相似,缺乏 Baseline 比较
Git Re-Basin 提出的第二个“新颖”方法是“检查模型本身的权重”,以对齐神经元。这是一个需要考虑的自然策略,事实上,类似的方法已经在过去的许多工作中使用过——可以追溯到 2015年 [1] 和 [2,3]。同样地,所有这些过去的方法也不需要依赖输入分布(例如,[3]的基于权重的对齐),可以在几秒钟内运行(参见下面的C.3节),这与 Git Re-Basin 传达的印象不同。
更具体地说,正如他们在工作中所说的,与基于激活的对齐相比,基于权重的匹配固有地提出了一个更复杂且很难精确地计算解决的双线性分配问题。之前的大多数工作 [1-3] 使用从输入层到输出层的贪心层对齐神经元。Git Re-Basin 采用了一种替代的方式,可能比上面的工作稍微好一点,尽管代价是计算和运行时间更昂贵。然而,不幸的是,Git Re-Basin 完全没有认识到这一点,并完全将这些相似之处掩盖起来。更不用说与之前的作品进行比较了!
此外,过去的工作 [2-4] 选择使用额外的计算在初始校准后进行微调/再训练(fine-tune/retrain),而非弥补任何缺点。这就引出了方法 3,他们使用“STE 估计器”,在寻找对齐和(猜猜是什么——)再训练之间交替进行一些迭代,比如一个 epoch(这里称为“向后传递”)。很明显,这种策略与文献 [2-4] 中使用的微调/再训练方法非常相似。事实上,还有两点可以说明这一点:
-
当与再训练相结合时,一开始只需一个基于权重的对齐方式就足够了,而不必在每一步之后都寻找全新的对齐方式,如 [3] 所示。在这种情况下,当作者在 STE 方法中也只执行一次基于权重的对齐时,是否会注意到任何显著的性能下降(如果有的话),这将很有趣了。 -
更令人惊讶的是,当融合两个网络时,[3] 还发现,简单地再训练幼稚或普通的网络表现具有竞争力。换句话说, 仅仅使用 identity 作为初始排列矩阵,并结合再训练(或STE方法的某些方式),可能相当有竞争力。
然而,作者们又一次没有进行这些比较,而是给他们的方法披上了一层新奇的外衣。包括了先前工作的 Baseline 可能会被质疑“新颖性”,对吧?

(C) 一些结果或观察结果已经以类似的形式为人所知
-
作者声称:
但我们想指出的是 [3] 的表 1,其中对于 CIFAR10 上的 ResNet18,已经表明 OTFusion(STE 一样进行再训练)获得了 的准确性,而单个网络的准确性为 和 。这应该表明两个独立训练的 Resnet 之间存在可忽略的势垒 LMC 的初步证据,因为 OTFusion 网络对应于插值曲线中的 ,这通常是与单个网络性能的最大偏差点(如图 2 所示)。
-
接下来,作者对此进行了讨论:
但是,[3]中有一整节详细说明(附录 S10 和表 S11)宽度如何降低全连接网络的性能差距(排列后)。这甚至是在[6]表明更广泛的模型在全连接和卷积网络中都表现出更好的 LMC 之前。此外,从[3]的表 S1 中还可以看到“模式连接时间”的新形式。由于 中的势垒定义为最大值除以 ,显然,势垒至少应该与表 S1 中描述的 的势垒一样大。
-
然后作者(错误地)声称他们是首个在几秒钟内找到解决方案的人:
考虑到他们的“新颖”算法只是炒过去工作 [1-4] 的“冷饭”,当 [3] 的第 5 页提到“在一个 Nvidia V100 GPU 上融合 6 个 VGG11 模型所需的时间≈15秒”时,这就不足为奇了。此外,在 S1.4 节中,[3] 详细说明了要融合两个网络,MLP 大约需要“3 秒”,CIFAR10 上 VGG11 大约需要“5 秒”,CIFAR10 上 ResNet18 大约需要“7 秒”。不幸的是,谎言又一次被传播开来。
-
此外,作者在第 5.4 节中指出,在不相交数据集上训练的模型可以被合并。然而,在 [3] 中完全相同的是,一页长的章节 5.1 演示了精确的事实!——审稿人 qnqB 也指出了这一点。但作为一种常见的模式,这里没有提及到这点,更别说进行任何比较了。

(D) “引用”相关工作的徒劳
同样,这显然不是建立在以前工作基础上的问题,但不以正确的方式提出它们,或像这里第 9 页第 3 段中那样油腔滑调地陈述它们,才是让人是不可接受的。
具体如下:
-
文献 [1,2] 未被引用。 -
那么 [3] 不是“通过软对齐关联权重合并模型”,而是明确表示“我们主要使用精确 OT 求解器”,因此他们获得了精确的排列矩阵(见 [3] 表 S4 中融合前对齐网络的准确性)。我们已经在上面的(A, B, C)部分中看到了与 [3] 的巨大相似性。 -
此外,[4] 的讨论表达得很奇怪,因为当他们的工作 [4] 中也说明了这一点时,不清楚为什么对他们来说融合等大小的网络会有问题。 -
最后, 简要地提到了 [5],但它们在模式连通性或算法相似性方面的主题相似程度被忽略了,正如审稿人 qnqB 所指出的那样。

小结
现在我们已经看清了 Git Re-Basin 的假象,很清楚,它当前的形式只是以前工作的翻版 [1-5],包含了通过在额外的网络规模和数据集(例如 MNIST、CIFAR10、CIFAR100 的结果已在 [2-6] 中显示)。
在这一点上,还需要庆幸 ICLR 是允许社区参与审查过程的独特会议之一,从而避免不准确的判断渗透到文献中——在其他会议中,只有在做了这些判断的情况下才能进行回顾性地更正。鉴于 ICLR 是现代科学进程的火炬手,并将维护科学的完整性,希望我们能够继续对ICLR公正和严谨的决策过程保持信心。
最后,这篇长文评论的两位作者Sidak Pal Singh 和 Martin Jaggi 表示很乐意详细说明或回答任何进一步的意见。
“听我说中药苦,抄袭应该更苦”,今天的这件事应当对我们有一些启发:应当学习 Sidak Pal Singh 博士对于学术道德的端正态度,诚然,在相关工作的基础上做研究是本没有错的,但必须诚实、不能欺骗、不能心存侥幸地隐瞒。
公众号后台回复“ECCV2022”获取论文资源分类汇总下载~

“
点击阅读原文进入CV社区
收获更多技术干货
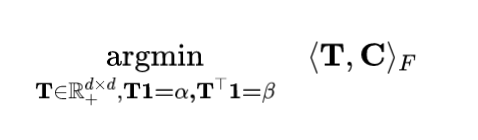

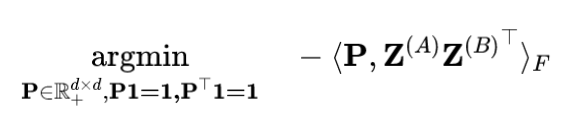

 但我们想指出的是 [3] 的表 1,其中对于 CIFAR10 上的 ResNet18,已经表明 OTFusion(STE 一样进行再训练)获得了
但我们想指出的是 [3] 的表 1,其中对于 CIFAR10 上的 ResNet18,已经表明 OTFusion(STE 一样进行再训练)获得了 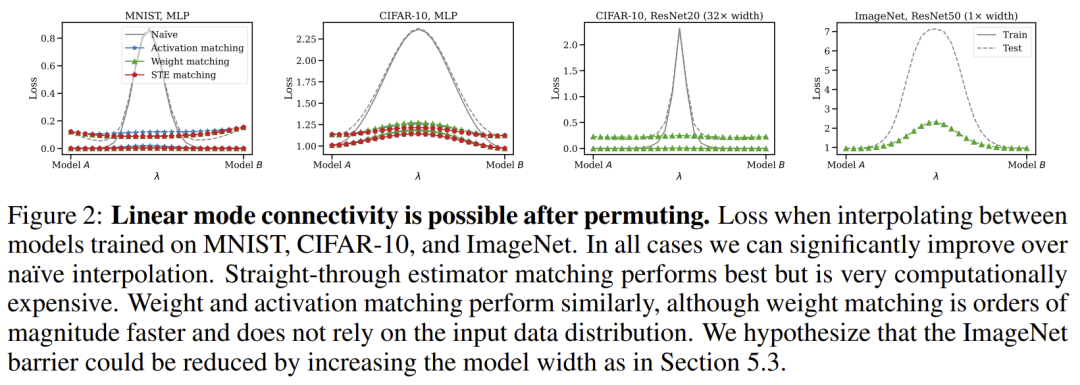
 但是,[3]中有一整节详细说明(附录 S10 和表 S11)宽度如何降低全连接网络的性能差距(排列后)。这甚至是在[6]表明更广泛的模型在全连接和卷积网络中都表现出更好的 LMC 之前。此外,从[3]的表 S1 中还可以看到“模式连接时间”的新形式。由于
但是,[3]中有一整节详细说明(附录 S10 和表 S11)宽度如何降低全连接网络的性能差距(排列后)。这甚至是在[6]表明更广泛的模型在全连接和卷积网络中都表现出更好的 LMC 之前。此外,从[3]的表 S1 中还可以看到“模式连接时间”的新形式。由于 
 考虑到他们的“新颖”算法只是炒过去工作 [1-4] 的“冷饭”,当 [3] 的第 5 页提到“在一个 Nvidia V100 GPU 上融合 6 个 VGG11 模型所需的时间≈15秒”时,这就不足为奇了。此外,在 S1.4 节中,[3] 详细说明了要融合两个网络,MLP 大约需要“3 秒”,CIFAR10 上 VGG11 大约需要“5 秒”,CIFAR10 上 ResNet18 大约需要“7 秒”。不幸的是,谎言又一次被传播开来。
考虑到他们的“新颖”算法只是炒过去工作 [1-4] 的“冷饭”,当 [3] 的第 5 页提到“在一个 Nvidia V100 GPU 上融合 6 个 VGG11 模型所需的时间≈15秒”时,这就不足为奇了。此外,在 S1.4 节中,[3] 详细说明了要融合两个网络,MLP 大约需要“3 秒”,CIFAR10 上 VGG11 大约需要“5 秒”,CIFAR10 上 ResNet18 大约需要“7 秒”。不幸的是,谎言又一次被传播开来。



