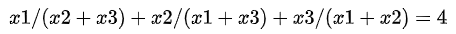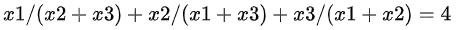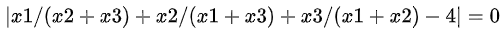用人工智能方法计算水果难题------遗传算法篇

2019 年 2 月 19 日 R语言中文社区

作者：梁凯 R语言中文社区专栏作者

知乎ID：https://www.zhihu.com/people/liang-kai-77-98

这次我们暂且不写爬虫，动态爬虫以后再写，因为这几天一直在纠结一个问题，这个问题就是水果难题，如图所示

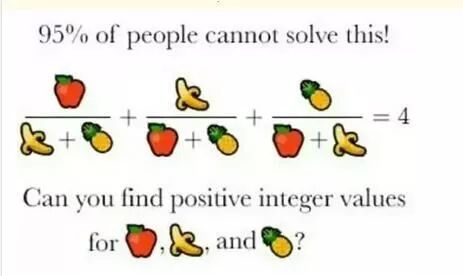
题目大言不惭说百分之九十五的人不能解决此问题，问题要我们找出苹果，香蕉，还有一个水果（是梨子？）的正整数解（positive integer values），看清楚是正整数解。小学生都知道我们要设X未知数，所以我们把水果看成X1,X2,X3，我们可以得到式1：

上面的例子我们把问题量化了，接下来怎么办？大学本科生都有可能不知道，因为我们去掉分母我们可以看出这是一个复杂的多元多次函数，而且只有一个式子看起来无法解（当然没有我们的贝叶斯参数式子复杂），在这里我们所需要做的就是找寻一种方法能让我们的式子得到有效解集，要求的是正整数，所以负数和非正整数都不是有效的。学过数值解析的数学专业学生或者统计专业学生很快就能想到用数值方法来接，学保险和金融工程等工程方面的学生很快就能想到用运筹方法来解。从理论上来说有纯数学方法来接，在计算机还没发明的时代，我们伟大的物理学家牛顿和数学家拉弗森发明了牛顿-拉弗森方法，这种方法是在理论上就是一步一步求函数的导数切线，一步步逼近真实解，在微积分方面就是要用泰勒级数展开，取前两项来进行迭代计算，当然这两种解释都是一种方法，但是我们更多的采用泰勒级数的解释方法，具体的可以参考网上各种牛顿-拉弗森方法（Newton-Raphson method）资料，这里不再详述，但是这一类方法有个最大的缺点就是函数可导还有计算量特别大，特别是当多元函数的时候我们必须要计算所有的黑塞矩阵（Hessian Matrix），这让我们感到十分费时费力。在计算机发展迅速的今天，我们有在人工智能上的成就，早就了很大一部分科学家创造出了有效的算法来解决一系列像这类问题一样的数学难题，特别是我们的人工智能算法，个人以为人工智能算法和数值方法还是有一系列区别的，人工智能算法很多都是仿生算法，学习自然界的算法，有的算法数学理论基础都还不是很完善，但是数值方法的数学理论基础是建立在数学和数理统计方法上的，数学理论很充实，人工智能算法虽然有效，但是人工智能算法就像我们实验设计中或者质量控制中的田口弘一先生田口方法与设计的正交实验设计表一样，无法得到一个统一的原理认识，但是它的确有效。

人工智能算法有很多是求解无约束优化问题和NP难题的，当然也有很多种用途，人工智能算法是仿生算法，所以大多数算法的启发来自自然界，也被称作启发式算法，如演算算法，遗传算法，群体智能算法，蚁群算法，蜂群算法，人工神经网络算法等，相比于我们的机器学习算法，这一类算法都比较复杂，但是一旦应用，就十分有效。拿我们的问题来说这里我们就用遗传算法和群体智能算法来解决问题。

问题量化

开始我们把问题量化成

这一种方法我们不能用于直接求解问题，因为我们要把问题转换成无约束优化问题来求解，我们稍加改变就可以得到

这里的取绝对值是因为我们需要把问题转换成无约束优化问题，而取绝对值等于零，无疑就是转化成了求这个式子的最小值，取绝对值就是最小值只能为0，也就是求x1，x2，x3取什么值时等于4.这么一来问题就被转化为求无约束优化问题了。

遗传算法求解

在人工智能算法中，除了人工神经网络算法，遗传算法是最有效而且比较成熟的方法之一，遗传算法的多变异性和遗传算子的设计能够有效时遗传算法跳出局部解而找到全局最佳解，并且合适的遗传算子选择设计能够缩短算法运行时间，使算法更加有效。遗传算法的局限性也相当明显，遗传算法最大的局限就在于算法自身的编码，对于一些问题来说遗传算法的编码过程很复杂，而且遗传算子的设计也是必须要参考到很多现实问题因素，所以我个人认为遗传算法不仅仅以一个算法来看待，而是应该像MCMC算法一样以一种系统方法来看待，遗传算法涉及的东西太多，大家有兴趣可以去看看专门的书籍，了解算法原理过程，算法原理理解并不太难。这里我们用R语言来进行算法的实现，R语言有遗传算法的包，一共两个。一个包叫作mcga包一个包叫做genalg包，下面我们分别使用两个包来求解。具体参数如下

mcga包

1mcga(popsize, chsize, crossprob = 1.0, mutateprob = 0.01, elitism = 1, minval, maxval, maxiter = 10, evalFunc)

参数解释：

popsize：个体数量，即染色体数目
chsize：基因数量，限参数的数量
crossprob：交配概率，默认为1.0
mutateprob：突变概率，默认为0.01
elitism：精英数量，直接复制到下一代的染色体数目，默认为1
minval：随机生成初始种群的下边界值
maxval：随机生成初始种群的上边界值
maxiter：繁殖次数，即循环次数，默认为10
evalFunc：适应度函数，用于给个体进行评价

因为需要得到精确值而不是近似值，所以我们要调整参数这里我们给出调好的参数程序大家可以试试

 1library(mcga)
 2library(GA)
 3library(foreach)
 4library(iterators)
 5
 6
 7
 8require("mcga")
 9
10f<-function(x){
11  return (abs(x[1]/(x[2]+x[3])+x[2]/(x[1]+x[3])+x[3]/(x[1]+x[2])-4))
12}
13
14m <- mcga( popsize=2000, 
15            chsize=3, 
16            minval=0.0, 
17            maxval=999999999, 
18            maxiter=25000, 
19            crossprob=1, 
20            mutateprob=0.01, 
21            evalFunc=f)
22
23
24print(m$population[1,])
25
26cat("Cost: ",m$costs[1],"\n")

这次我们得到的值为

853989867 189086360 38573036

大家可以看出非常大的数值

genalg包

1rbga(stringMin=c(), stringMax=c(),
2suggestions=NULL,
3popSize=200, iters=100,
4mutationChance=NA,
5elitism=NA,
6monitorFunc=NULL, evalFunc=NULL,
7showSettings=FALSE, verbose=FALSE)

参数解释

stringMin，设置每个基因的最小值
stringMax，设置每个基因的最大值
suggestions，建议染色体的可选列表
popSize，个体数量，即染色体数目，默认为200
iters，迭代次数，默认为100
mutationChance，突变机会，默认为1/(size+1)，它影响收敛速度和搜索空间的探测，低机率导致更快收敛，高机率增加了搜索空间的跨度。
elitism，精英数量，默认为20%，直接复制到下一代的染色体数目
monitorFunc，监控函数，每产生一代后运行
evalFunc，适应度函数，用于给个体进行评价
showSettings，打印设置，默认为false
verbose，打印算法运行日志，默认为false

这里我们的程序为

 1ibrary(genalg)
 2
 3m2 = rbga(c(0,0,0),
 4          c(999999999,999999999,999999999),
 5          popSize=2000,
 6          iters=25000,
 7          evalFunc=f,
 8          mutationChance=0.01,
 9          verbose=F,
10          #monitorFunc=monitor
11          )
12
13print(m2$population[1,])
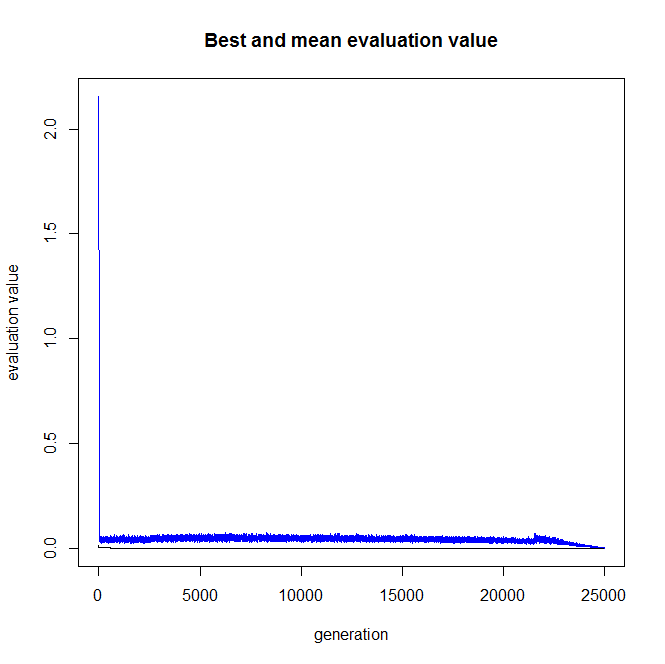
14plot(m2)

注意：这里我们的群体和迭代次数和我们上一个包一样，但是运行时间很长，得到的结果

101041126 137623799 898526155

这里近似4，真实值为4.000001，可以看出第二个包的效率明显比第一个低

可以看出收敛到最小值非常缓慢25000次末端的时候才搜索到。

往期精彩：

公众号后台回复关键字即可学习

回复爬虫            爬虫三大案例实战
回复 Python       1小时破冰入门
回复数据挖掘     R语言入门及数据挖掘
回复人工智能     三个月入门人工智能
回复数据分析师  数据分析师成长之路
回复机器学习     机器学习的商业应用
回复数据科学     数据科学实战
回复常用算法常用数据挖掘算法