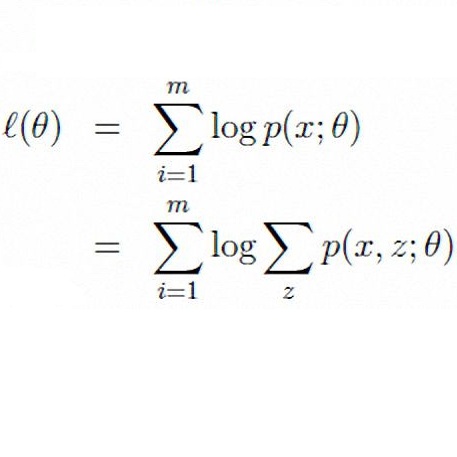深入机器学习系列之:隐式狄利克雷分布(2)


导读
在上一篇推送中,为大家介绍了LDA的数学预备知识以及LDA主题模型,今天将带来有关LDA 参数估计和LDA代码的实现。
来源: 星环科技
数据猿官网 | www.datayuan.cn

今日头条丨一点资讯丨腾讯丨搜狐丨网易丨凤凰丨阿里UC大鱼丨新浪微博丨新浪看点丨百度百家丨博客中国丨趣头条丨腾讯云·云+社区

3
LDA 参数估计
在spark中,提供了两种方法来估计参数,分别是变分EM(期望最大)算法(见文献【3】【4】)和在线学习算法(见文献【5】)。下面将分别介绍这两种算法以及其源码实现。
3.1 变分EM算法
变分贝叶斯算法的详细信息可以参考文献【9】。
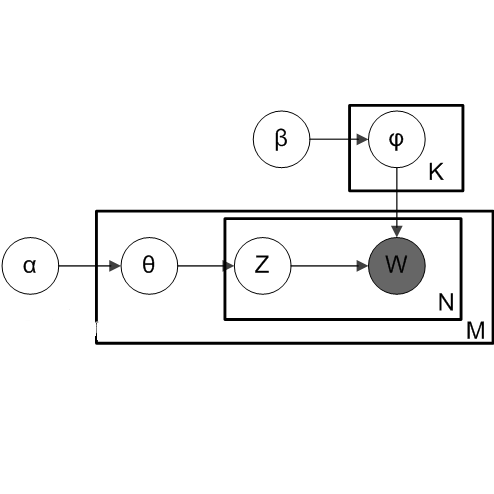
在上文中,我们知道LDA将变量theta和phi(为了方便起见,我们将上文LDA图模型中的beta改为了phi)看做随机变量,并且为theta添加一个超参数为alpha的Dirichlet先验,为phi添加一个超参数为eta的Dirichlet先验来估计theta和beta的最大后验(MAP)。 可以通过最优化最大后验估计来估计参数。我们首先来定义几个变量:

根据文献【4】中2.2章节的介绍,我们可以推导出如下更新公式,其中alpha和eta均大于1:
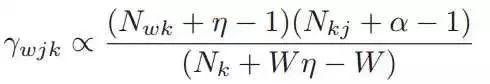
收敛之后,最大后验估计可以得到公式:
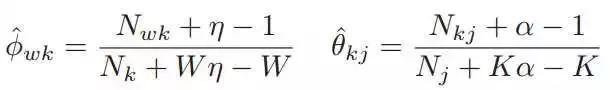
变分EM算法的流程如下:

第4.2章会从代码层面说明该算法的实现流程。
3.2 在线学习算法
3.2.1 批量变分贝叶斯
在变分贝叶斯推导(VB)中,根据文献【3】,使用一种更简单的分布q(z,theta,beta)来估计真正的后验分布,这个简单的分布使用一组自由变量(free parameters)来定义。 通过最大化对数似然的一个下界(Evidence Lower Bound (ELBO))来最优化这些参数,如下公式:
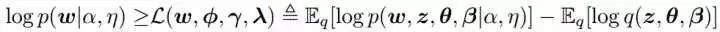
最大化ELBO就是最小化q(z,theta,beta)和p(z,theta,beta|w,alpha,eta)的KL距离。根据文献【3】,我们将q因式分解为如下的形式:
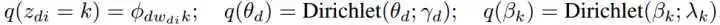
后验z通过phi来参数化,后验theta通过gamma来参数化,后验beta通过lambda来参数化。为了简单描述,我们把lambda当作“主题”来看待。公式分解为如下形式:
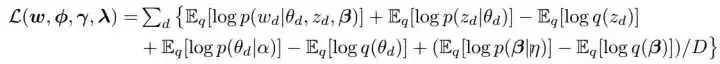
我们现在将上面的期望扩展为变分参数的函数形式。这反映了变分目标只依赖于 ,即词w出现在文档d中的次数。当使用VB算法时,文档可以通过它们的词频来汇总(summarized),如公式:
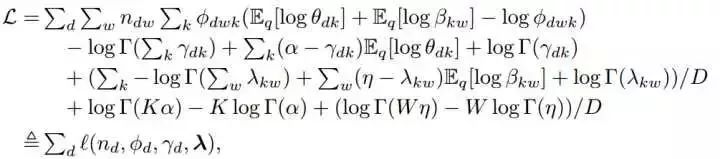
上面的公式中,W表示词的数量,D表示文档的数量。l表示文档d对ELBO所做的贡献。L可以通过坐标上升法来最优化,它的更新公式如:
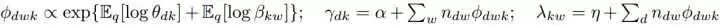
log(theta)和log(beta)的期望通过下面的公式计算:
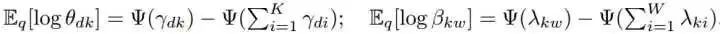
通过EM算法,我们可以将这些更新分解成E-步和M-步。E-步固定lambda来更新gamma和phi;M-步通过给定phi来更新lambda。批VB算法的过程如下所示:

3.2.2 在线变分贝叶斯
批量变分贝叶斯算法需要固定的内存,并且比吉布斯采样更快。但是它仍然需要在每次迭代时处理所有的文档,这在处理大规模文档时,速度会很慢,并且也不适合流式数据的处理。 文献【5】提出了一种在线变分推导算法。设定gamma(n_d,lambda)和phi(n_d,lambda)分别表示gamma_d和phi_d的值,我们的目的就是设定phi来最大化下面的公式:
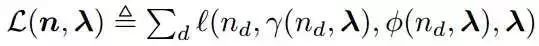
我们在算法2中介绍了在线VB算法。因为词频的第t个向量是可观察的,我们在E-步通过固定lambda来找到gamma_t和phi_t的局部最优解。 然后,我们计算lambda_cap。如果整个语料库由单个文档重复D次组成,那么这样的lambda_cap设置是最优的。之后,我们通过lambda之前的值以及lambda_cap来更新lambda。我们给lambda_cap设置的权重如公式所示:
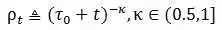
在线VB算法的实现流程如下算法2所示:

那么在在线VB算法中,alpha和eta是如何更新的呢?参考文献【8】提供了计算方法。给定数据集,dirichlet参数的可以通过最大化下面的对数似然来估计:
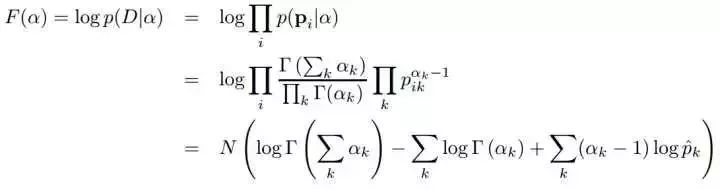
其中
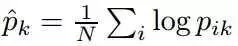
有多种方法可以最大化这个目标函数,如梯度上升,Newton-Raphson等。Spark使用Newton-Raphson方法估计参数,更新alpha。Newton-Raphson提供了一种参数二次收敛的方法, 它一般的更新规则如下公式:
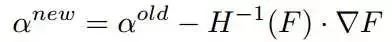
其中,H表示海森矩阵。对于这个特别的对数似然函数,可以应用Newton-Raphson去解决高维数据,因为它可以在线性时间求出海森矩阵的逆矩阵。一般情况下,海森矩阵可以用一个对角矩阵和一个元素都一样的矩阵的和来表示。 如下公式,Q是对角矩阵,C11是元素相同的一个矩阵。
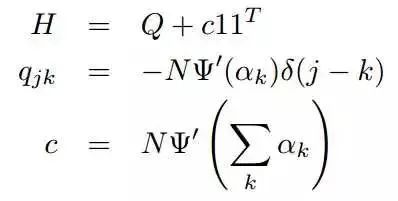
为了计算海森矩阵的逆矩阵,我们观察到,对任意的可逆矩阵Q和非负标量c,有下列式子:
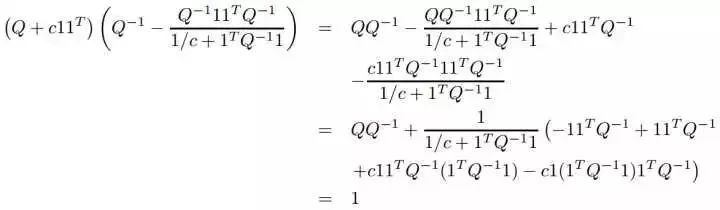
因为Q是对角矩阵,所以Q的逆矩阵可以很容易的计算出来。所以Newton-Raphson的更新规则可以重写为如下的形式:
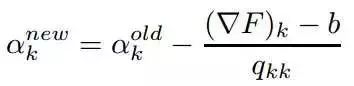
其中b如下公式:
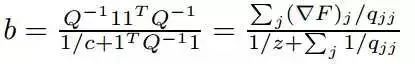
4
LDA代码实现
4.1 LDA使用实例
我们从官方文档【6】给出的使用代码为起始点来详细分析LDA的实现。
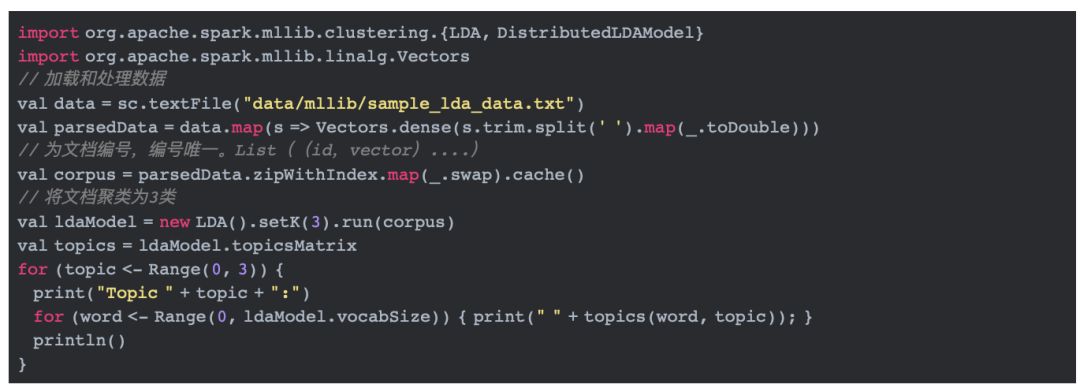
以上代码主要做了两件事:加载和切分数据、训练模型。在样本数据中,每一行代表一篇文档,经过处理后,corpus的类型为List((id,vector)*),一个(id,vector)代表一篇文档。将处理后的数据传给org.apache.spark.mllib.clustering.LDA类的run方法, 就可以开始训练模型。run方法的代码如下所示:
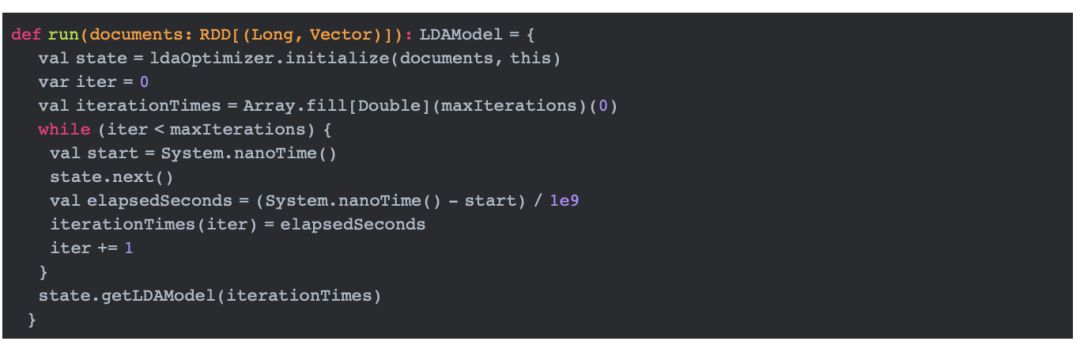
这段代码首先调用initialize方法初始化状态信息,然后循环迭代调用next方法直到满足最大的迭代次数。在我们没有指定的情况下,迭代次数默认为20。需要注意的是, ldaOptimizer有两个具体的实现类EMLDAOptimizer和OnlineLDAOptimizer,它们分别表示使用EM算法和在线学习算法实现参数估计。在未指定的情况下,默认使用EMLDAOptimizer。
4.2 变分EM算法的实现
在spark中,使用GraphX来实现EMLDAOptimizer,这个图是有两种类型的顶点的二分图。这两类顶点分别是文档顶点(Document vertices)和词顶点(Term vertices)。
·文档顶点使用大于0的唯一的指标来索引,保存长度为k(主题个数)的向量
·词顶点使用{-1, -2, ..., -vocabSize}来索引,保存长度为k(主题个数)的向量
·边(edges)对应词出现在文档中的情况。边的方向是document -> term,并且根据document进行分区
我们可以根据3.1节中介绍的算法流程来解析源代码。
4.2.1 初始化状态
spark在EMLDAOptimizer的initialize方法中实现初始化功能。包括初始化Dirichlet参数alpha和eta、初始化边、初始化顶点以及初始化图。

上面的代码初始化了超参数alpha和eta,根据文献【4】,当alpha未指定时,初始化其为(50.0 / k) + 1.0,其中k表示主题个数。当eta未指定时,初始化其为1.1。
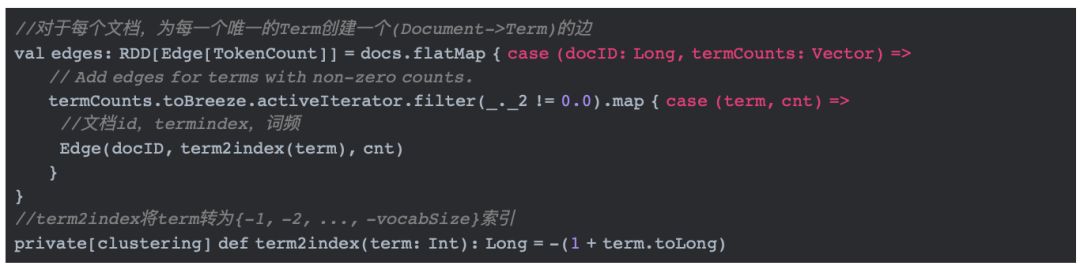
上面的这段代码处理每个文档,对文档中每个唯一的Term(词)创建一个边,边的格式为(文档id,词索引,词频)。词索引为{-1, -2, ..., -vocabSize}。

上面的代码创建顶点。我们为每个主题随机初始化一个值,即gamma是随机的。sum为gamma * edge.attr,这里的edge.attr即N_wj,所以sum用gamma * N_wj作为顶点的初始值。

上面的代码初始化Graph并通过文档分区。
4.2.2 E-步:更新gamma

上述代码中,W表示词数,N_k表示所有文档中,出现在主题k中的词的词频总数,后续的实现会使用方法computeGlobalTopicTotals来更新这个值。N_wj表示词w出现在文档j中的词频数,为已知数。E-步就是利用公式去更新gamma。 代码中使用computePTopic方法来实现这个更新。edgeContext通过方法sendToDst将scaledTopicDistribution发送到目标顶点, 通过方法sendToSrc发送到源顶点以便于后续的M-步更新的N_kj和N_wk。下面我们看看computePTopic方法。
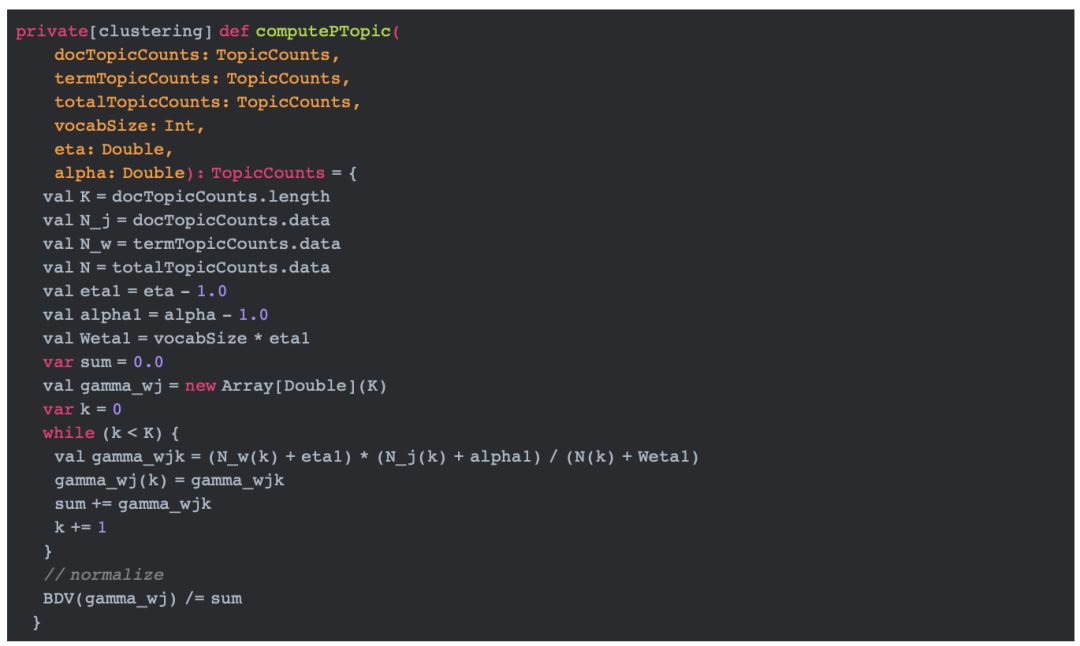
这段代码比较简单,完全按照公式**(3.1.6)**表示的样子来实现。val gamma_wjk = (N_w(k) + eta1) * (N_j(k) + alpha1) / (N(k) + Weta1)就是实现的更新逻辑。
4.2.3 M-步:更新phi和theta

更新隐藏变量phi和theta就是更新相应的N_kj和N_wk。聚合更新使用aggregateMessages方法来实现。请参考文献【7】来了解该方法的作用。
4.3 在线变分算法的代码实现
4.3.1 初始化状态
在线学习算法首先使用方法initialize方法初始化参数值。
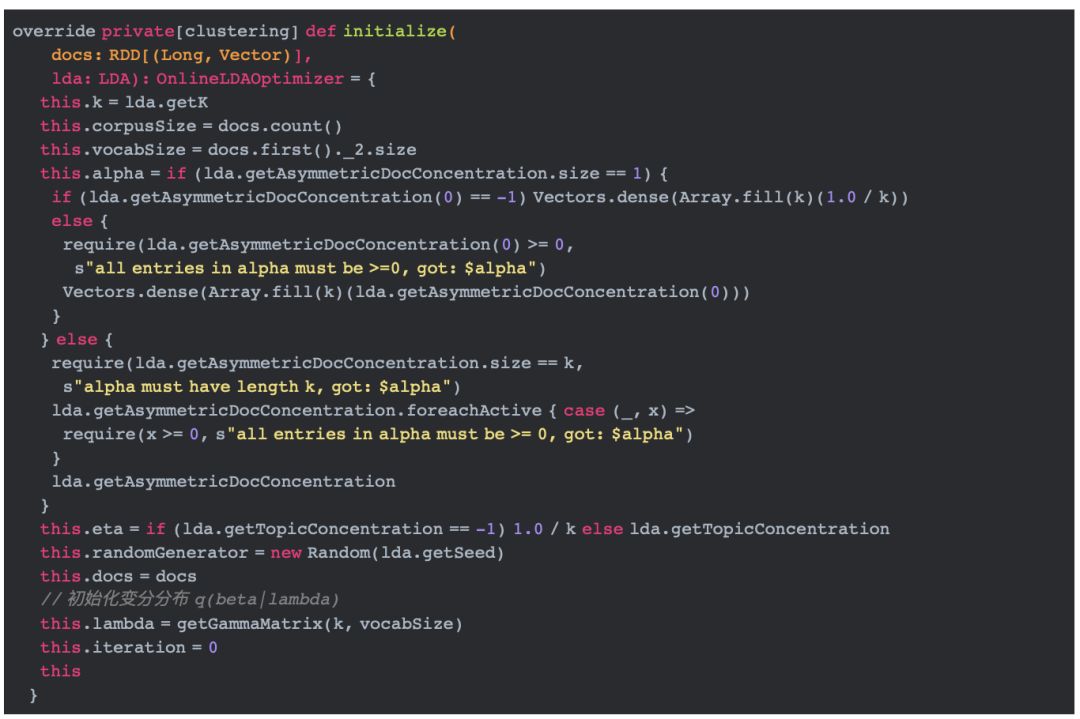
根据文献【5】,alpha和eta的值大于等于0,并且默认为1.0/k。上文使用getGammaMatrix方法来初始化变分分布q(beta|lambda)。

getGammaMatrix方法使用gamma分布初始化一个随机矩阵。
4.3.2 更新参数
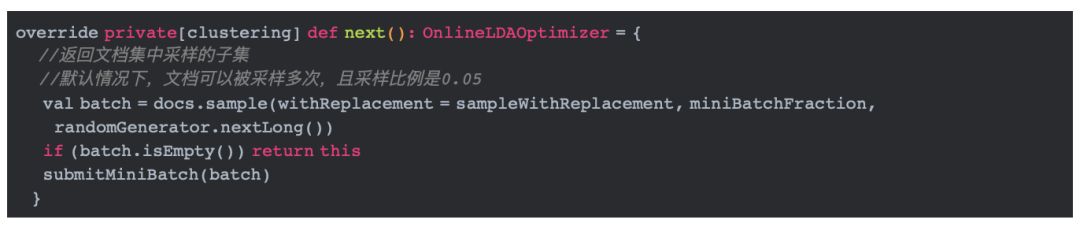
以上的next方法首先对文档进行采样,然后调用submitMiniBatch对采样的文档子集进行处理。下面我们详细分解submitMiniBatch方法。
·1 计算log(beta)的期望,并将其作为广播变量广播到集群中
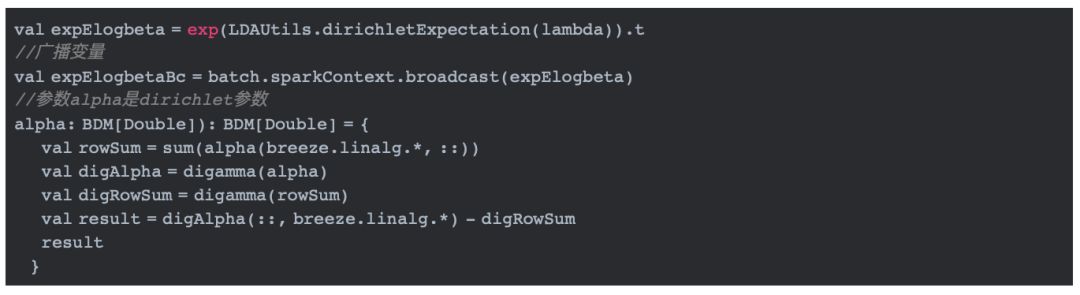
上述代码调用exp(LDAUtils.dirichletExpectation(lambda))方法实现参数为lambda的log beta的期望。
·2 计算phi以及gamma,即算法2中的E-步
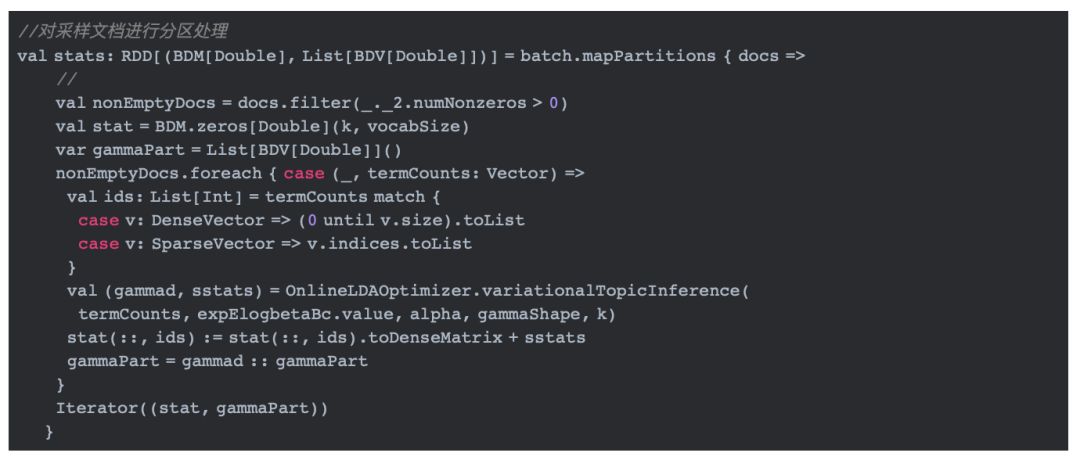
上面的代码调用OnlineLDAOptimizer.variationalTopicInference实现算法2中的E-步,迭代计算phi和gamma。
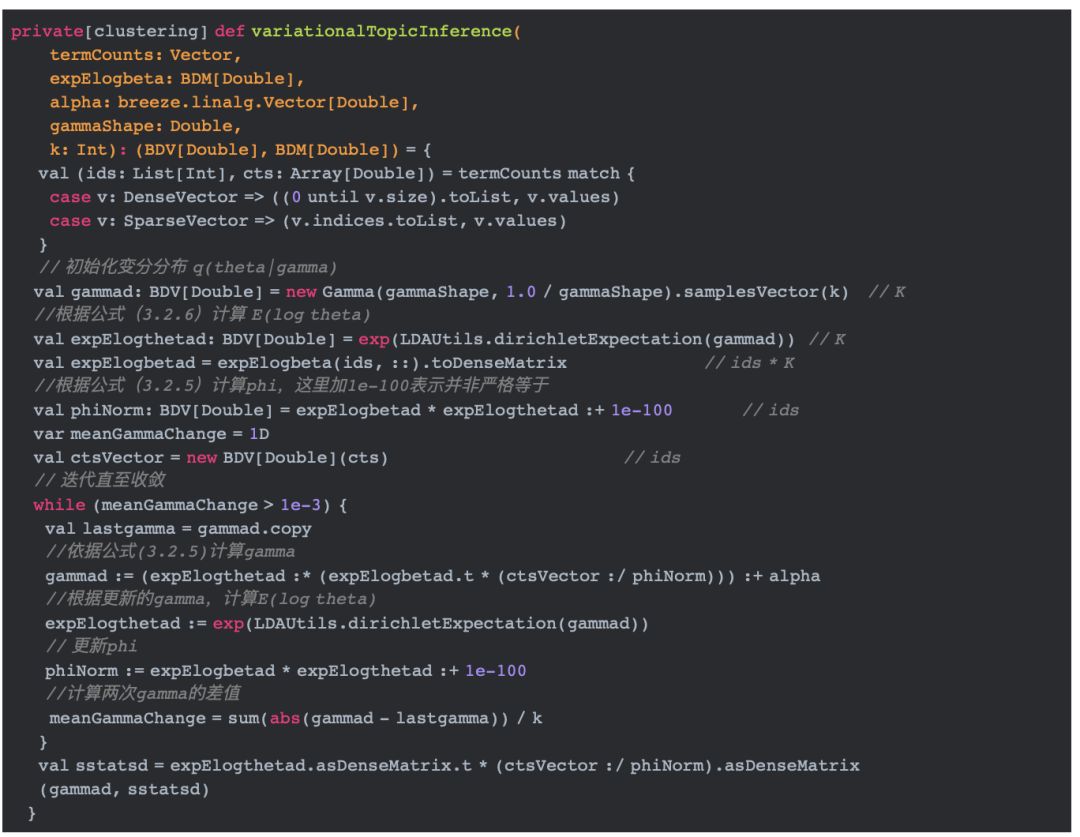
·3 更新lambda

updateLambda方法实现算法2中的M-步,更新lambda。实现代码如下:

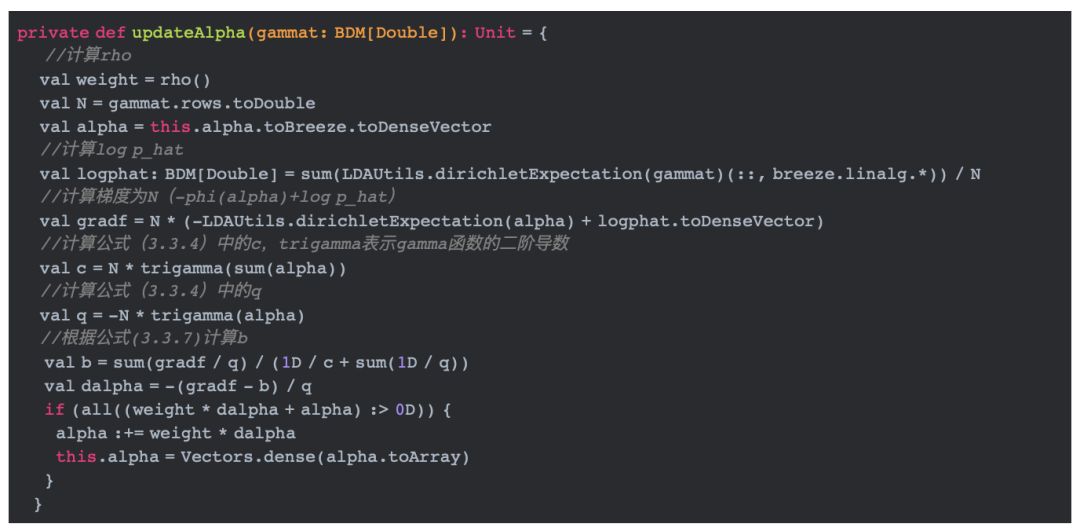
·4 更新alpha