【博士论文】多视光场光线空间几何模型研究

2021 年 12 月 6 日 专知

来自西北工业大学张　琦的博士论文，入选2021年度“CCF优秀博士学位论文奖”初评名单！

https://www.ccf.org.cn/Focus/2021-11-22/750448.shtml

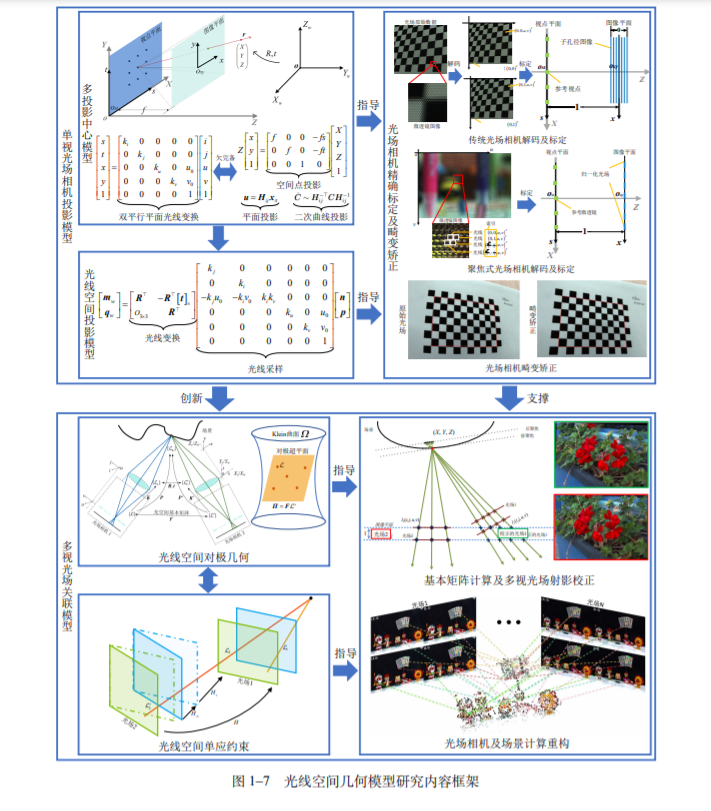
多视光场光线空间几何模型研究

光场以空间光线为基本单元，通过对光线位置和角度信息进行采样，可实现重聚焦、变视点、扩展景深等新颖应用，是计算机视觉与计算摄像学的重要理论创新点和技术突破口。但是，现有光场成像理论存在投影模型不统一、光场成像装置存在空间和角度分辨率折衷等问题，尚无法满足应用需求。本文以多视光场为研究对象，从光场相机投影模型出发，重点研究光场相机光线采样及变换过程，分析其对场景三维结构的影响。另一方面，本文从 Plücker 光线出发，重点研究光线空间对极几何，分析多视光场内在射影关系，进而研究多视光场相机自标定和三维重建方法。论文研究工作的主要创新点包括：（1）提出了统一描述异构光场相机的多投影中心模型。从传统相机的中心投影模型出发，推导了三维空间点投影变换矩阵，提出了隐含视点偏移的光场相机畸变模型，实现了基于空间点的光场相机标定方法。此外，分析了多投影中心模型对平面和二次曲线的映射，推导了共心二次曲线的共自配极三角形，阐述了其性质并在光场中重建共自配极三角形，实现了基于共心二次曲线的光场相机标定方法。仿真与真实光场数据的实验结果表明，多投影中心模型可统一描述光场相机的异构特性，并利用不同标定物精确标定光场相机。

（2）提出了统一描述光场相机光线采样及变换的光线空间投影模型。从 Plücker 光线出发，提出了 6 × 6 光线空间内参矩阵和投影矩阵，分别描述了光场相机光线采样和变换过程。根据 Plücker 光线的数学定义，推导了其在 Klein 曲面的高维特性及光线空间投影变换的不变性。基于光线空间投影矩阵，建立了空间点与光线间线性约束，提出了光场相机标定方法，定义了异面光线间几何距离，并用于非线性优化。仿真与真实光场数据的实验结果表明，光线空间投影模型可统一描述光线采样及变换过程，并精确标定光场相机。

（3）提出了描述多视光场关联关系的光线空间对极几何。从光线空间投影模型出发，研究了光线空间对极几何，描述了二视图光场间内在射影几何，其独立于场景结构，只依赖于光场相机的内外参数，推导了 6 × 6 光线空间基本矩阵，并给出其性质。通过分析光线空间基本矩阵的正交性约束和奇异性约束，提出了光线空间基本矩阵计算方法，定义了光线对称对极距离，并用于非线性优化。通过仿真与真实光场数据的实验，验证了光线空间基本矩阵计算方法的准确性与可靠性，展示了光线空间对极几何对于多视光场应用的理论指导意义。

（4）提出了多视光场相机自标定和三维重建方法。从光线空间对极几何出发，构建了 6 × 6 光线空间单应，描述了多视光场间同一光线的关联性关系，分解了仅与旋转矩阵相关的光线空间无穷单应，推导了绝对二次曲线的光线束。根据光线空间无穷单应的旋转共轭，计算光线空间无穷单应，估计光场相机内参数及相对姿态，定义了光线间 Sampson 距离，并用于非线性优化，最终实现光场相机及场景的计算重构。仿真与真实数据的实验结果表明，所提算法在精确重构光场相机投影矩阵的同时，可直接从多视光场实现三维重建。