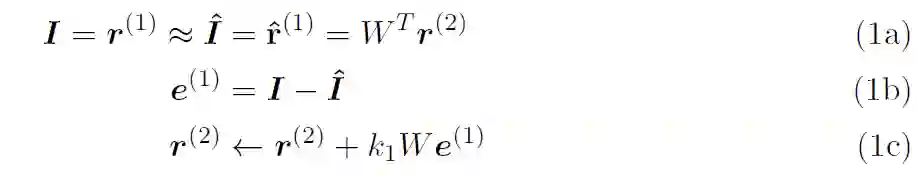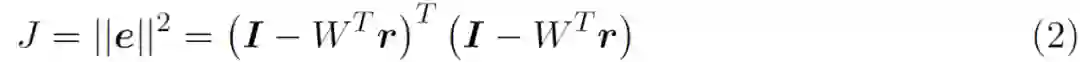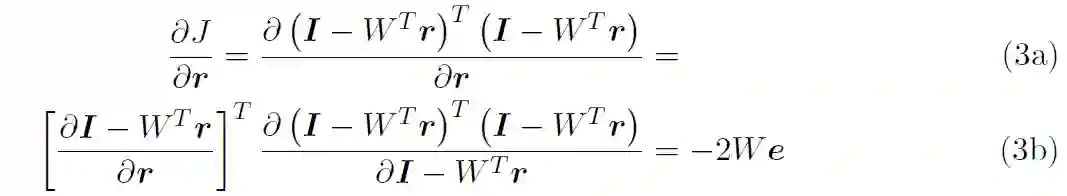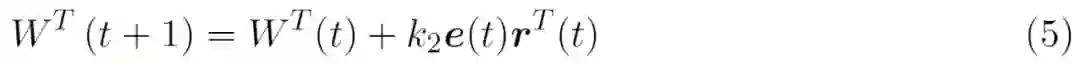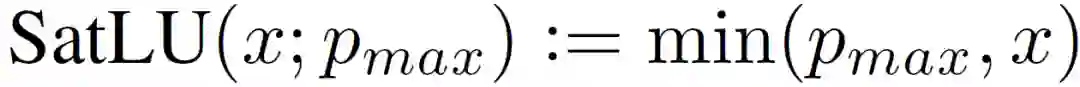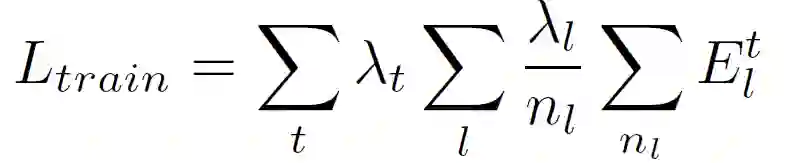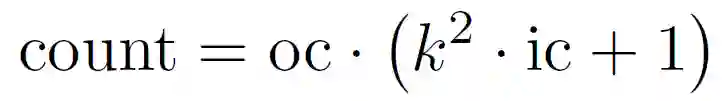说到深度学习架构中的预测编码模型，还得看PredNet

 机器之心分析师网络

作者：仵冀颖

编辑：Joni

本文中，作者对经典预测编码模型和深度学习架构中的预测编码模型进行了简单回顾，其中重点介绍了用于视频预测和无监督学习的深度预测编码网络 PredNet 以及基于 PredNet 进行改进的一些版本。

0、 引言

预测编码（predictive coding）是一种认知科学的假说。与一般认为高层次的神经活动都是由感官输入引起的理念不同，该假说认为更高层次的神经表征会参与定义感觉输入（Sensory Input）。预测编码的概念起源于神经科学界，近年来，机器学习领域的一些研究人员也开始致力于研究预测编码相关的模型。本文以来自路易斯安那大学拉菲特分校（University of Louisiana at Lafayette） 的 Hosseini M 和 Maida A 近期发表的文章为基础[1]，探讨预测编码是如何在深度学习的架构中应用的。

预测编码的一个决定性特征是：它使用自上而下的重构机制来预测感觉输入或其低级别的表征。具体来说，预测编码首先确定预测值和实际输入之间的差异（称为预测误差），然后启动后续学习过程，以改进所学的更高层次表征的预测准确度。在深度学习发展之前，旨在描述新皮质计算（computations in the neocortex）的预测编码模型就已经出现，这些模型构建了模块之间的通信结构，称之为 Rao-Ballard 协议（RB protocol）。RB 协议是由贝叶斯生成模型得出的（通过结合感觉输入与先前的预期，以做出更好的未来预测），包含了一些强统计假设。而非贝叶斯预测编码模型（不遵循 RB 协议）一般用于减少信息传输要求和取消自身行动的影响，而不是用于预测。

预测编码可以看作是一种表征学习（representation learning）。支持贝叶斯预测编码的学习机制能够改进所获取的内部表征的质量，这可以看做是减少未来预测误差的一种副作用。预测 / 重构能力确保获得的表征能够完全代表输入中所包含的信息。由于整个学习过程是由预测误差所驱动的，所以是一种无监督学习，只需要预测的数据流的信息。

在应用方面，预测编码可用于学习重叠图像组件、物体分类、视频预测、视频异常检测、偏向竞争（Bias competition）建模、灵长类视觉皮层的反应特性以及脑电图诱发的大脑反应健康问题。此外，它还被提出作为新皮层功能的统一理论。

到目前为止，在深度学习架构中构建大型的预测编码模型的示例非常少见，最著名的为文献 [3] 中提出的 PredNet 模型，我们会在文章中对其进行介绍。大多数预测编码模型都是在深度学习框架出现之前实现的，所以这些经典的模型规模都很小，而且都没有专门的时间处理模块。

1、 预测编码的基本知识

首先，我们参考来自华盛顿大学的研究人员发表的一篇预测编码综述性文章，从神经学的角度对预测编码进行介绍 [2]。预测编码是一个试图解释认知现象和理解神经系统的统一框架，它提出了神经系统中如何减少冗余和进行高效编码：通过只传输传入的感觉信号中未预测的部分，预测编码允许神经系统减少冗余并充分利用神经元的有限动态范围。预测编码为一系列神经反应和大脑组织的许多方面提供了功能性解释。自然界中视网膜和外侧膝状核（lateral geniculate nucleus，LGN）接受区(receptive field) 的侧向和时间拮抗（temporal antagonism）是自然图像预测编码的结果。在预测编码模型中，视网膜 / LGN 中的神经回路主动地从空间中的附近值或时间中的先验输入值的线性加权总和来预测局部强度的数值。这些电路中的细胞传达的不是原始图像强度，而是预测值和实际强度之间的差异，这种处理方式减少了输出冗余。而在高级视觉系统中，预测编码为定向感受区和背景效应以及大脑皮层的分层互连组织提供了解释。从不同脑区获得的各种神经生理学和心理物理学数据也与预测编码的猜想一致。

我们先了解一下不同层级的神经系统的响应特点：大脑中初级视觉皮层（V1）的神经元对特定方向的条形和边缘作出反应，而 V2 和 V4 区的神经元对更复杂的形状和轮廓特征作出反应。内侧颞上区（medial superior temporal，MST）的神经元对视觉运动有反应。这些反应的选择性可以从自然输入的分层预测编码的角度来理解。例如，由于视觉系统是分层组织的，皮层区域之间有相互的联系。根据 Rao 和 Ballard 提出的分层神经网络的架构（RB 架构），来自高阶视觉皮层区域的自上而下的反馈连接承载了对低阶神经活动的预测，而自下而上的连接则传达了预测的剩余误差。在对取自自然场景的图像斑块进行模型网络训练后，他们发现模型神经元发展出与 V1 相似的感受野特性，包括定向感受野、末端停顿和其他背景效应。

预测编码的一个早期应用是创建视网膜的模型，这些模型具有较低的信息传输要求，因为视神经是向大脑传输视觉信息的瓶颈。连续的视觉输入具有高冗余度。如果视网膜上的细胞从空间上和时间上计算出传入光线的移动平均值，就可以得到对当前输入的预测。通过将实际输入与预测进行比较，视网膜可以将预测误差发送到后来的处理区域，从而减少传输带宽。如果脊椎动物的视网膜从头开始创建当前输入图像的表征，信息传输的要求将取决于建立当前环境的完整表征所需的带宽。然而，大脑通常可以利用其对过去环境的现有表征以及关于环境如何变化的约束条件，对环境的当前状态做出非常好的预测。与从头开始建立当前环境状态的表征相比，预测误差只需要较少的带宽来表示。如果大脑已经有了一个相当准确的默认预测，那么用预测误差来更新默认预测就可以创造一个最新的、信息传输需求较低的表征。此外，预测误差可以提供很好的信息来指导学习，以改善表征并减少未来的预测误差。

随着预测编码模型的发展，人们开始尝试将其构建为生成模型，以使其能够直接生成预测的感觉输入。这通常将其表示为一个层次结构，其中上层预测下层的输出（即对上层的输入），任何预测误差都提供信息来指导上层的学习。涉及前馈和反馈连接的分层结构也与灵长类动物的新皮层结构一致。在感知推理和识别的背景下，一个训练好的生成模型具有这样的特性：学习到的表征可以重建原始感觉输入的分布，并在不同的空间和时间尺度上估计输入中的隐性原因。学习到的表征能够捕捉到首先产生输入的因果因素，因此使得重建变为可能。它需要一个从感觉到原因的逆向映射，以便构建表征。这很有挑战性，因为计算物理世界中感觉和原因之间的逆向映射是一个 ill-posed 问题，也就是说，它的解决方案不是唯一的。在贝叶斯方法中，这可以通过使用适当的先验概率来解决，在某些情况下，如果有足够的输入，可以学习这些先验概率。一种方法是通过学习使预测误差最小化（即预测性编码）。

早期的预测编码模型一般被表述为统计模型，如分层期望最大化（hierarchical expectation maximization）和变分自由能量模型（variational free energy models）。尽管这些模型提出了计算预测的精确计算方法但仍存在一些问题和挑战，实施这些模型具有非常庞大的计算量，而且模型的假设具有高度的限制性。在近期的研究工作中，研究人员提出了利用深度神经网络结构来解决这一问题[3]，从而可以直接调用深度学习框架附带的大型工具集已解决计算量的问题。

2、 预测编码学习层次化的背景知识[1][5]

本节我们首先了解一下经典的预测编码方法是如何学习层次化的背景知识的。如上一节中分析，人类的大脑通常可以利用其对过去环境的现有表征以及关于环境如何变化的约束条件，对环境的当前状态做出非常好的预测。而预测编码模型则是通过生成方式来预测感觉输入。一般的，这种生成方式构建为一个 层次化的结构：上层预测下层的输出（即上层的输入），任何预测误差都提供信息来指导上层的学习 。预测编码模型通过减少各层的预测误差来构建层次化的表征，即 表征层次结构（Representation hierarchies） ，具体包括两类方法：第一类方法是构建越来越抽象的特征层次，通过在层次结构的后期使用更大的输入上下文信息（input context）来实现，类似于卷积网络。第二类方法是像在泰勒级数展开中一样学习高阶误差的层次结构。我们在这一章节具体介绍一种第一类方法，即 Rao/Ballard 模型。

Rao/Ballard 的经典文献 [5] 中使用三级表示层次结构对初级视皮层末梢神经感受野模型进行建模，其中来自更上层的反馈传达对前一层神经活动的预测。例如，将最下层的预测活动与实际活动（原始感官输入）进行比较。预测误差是一个层的输出，并被转发到下一个更高的层。在层次结构中，有两类神经元：内部表示神经元和预测误差神经元。在预测中间层表征时，通过让最上层表征使用相邻的空间上下文对结束停止（End-stopping）进行建模。最上层表征为空间更大的上下文构建表示。该模型是围绕预测元素（predictive element，PE）建立的。人们可以将预测元素视为大脑中的一个处理阶段或皮质层。在深度学习术语中，它由两个执行互补功能的神经层组成，并通过前馈和反馈连接连接。

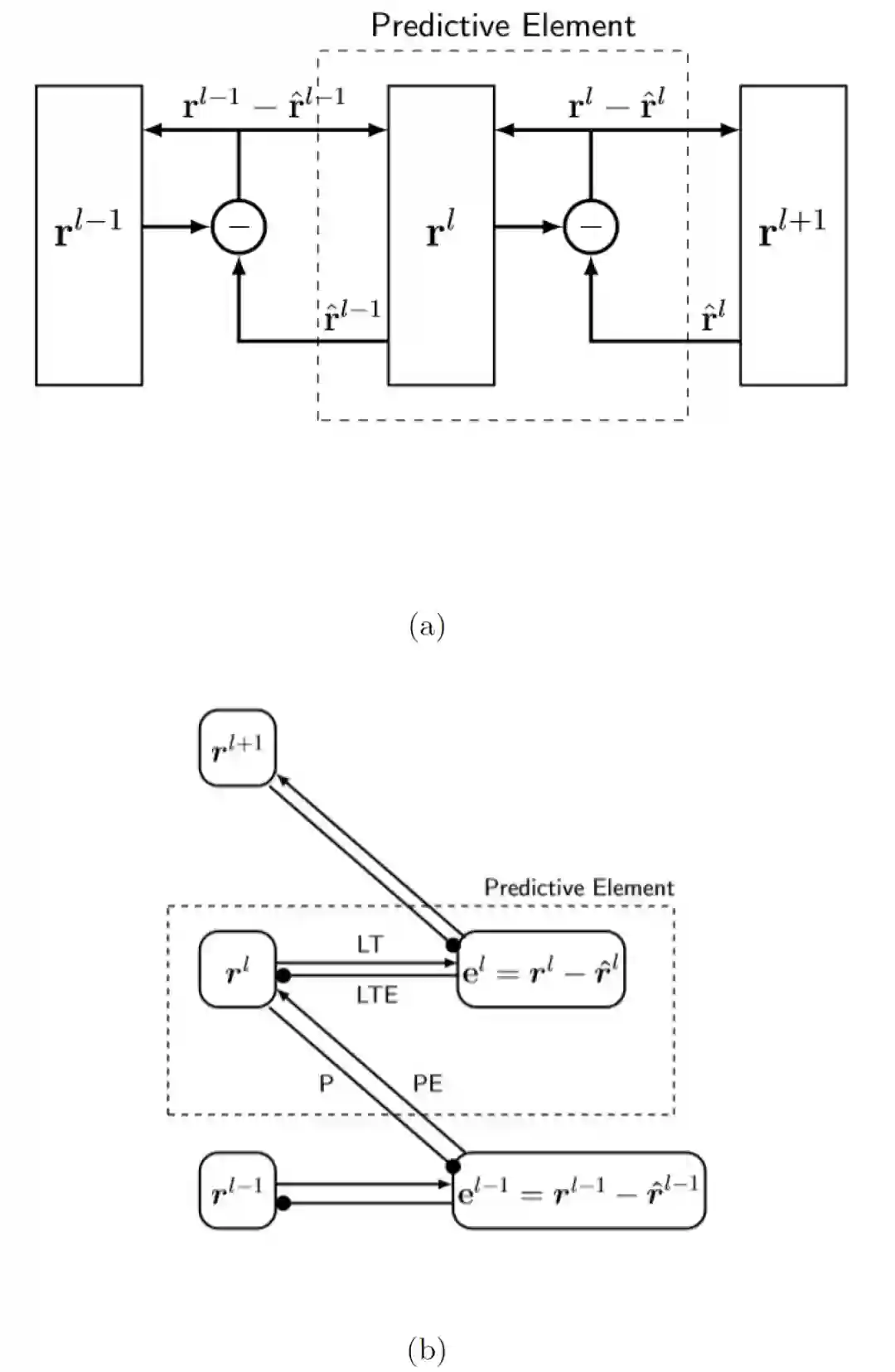
为了方便理解，我们给出 PE 的图形化展示。将 PE 堆叠成层次结构（图 1（a））。PE 从层次结构中的前一层接收预测误差（通过前向连接），并以先验概率的形式（通过后向连接）向前一层发送预测。图 1（a）给出信息流的原始视图。第 l+1 层学习第 l 层的变换表示，从而提高其对第 l 层活动的预测性能。r(l)表示输入的假设原因。不同的层 l 以越来越高的描述级别提供相同原因的不同表示。每一层的表达都表现为形成该层的神经元向量的一组激活水平。图 1（b）中的视图显示相邻层之间的交互遵循一个约束协议，即 Rao-Ballard 协议。在我们的表示中，有四种连接类型：预测（prediction，P）、预测误差（prediction error，PE）、横向目标（lateral target，LT）和横向目标误差（lateral target error，LTE）。层输出是由 PE 连接提供的信息。P 和 PE 为完全连接，LT 和 LTE 为点对点连接（见图 2）。表示模块仅与预测误差模块通信，预测误差模块仅与表示模块通信。此外，预测误差神经元在层次结构中从不向下投射，内部表征神经元在层次结构中从不向上投射。

图 1：（a）预测 PE 的 Rao/Ballard 图。虚线框中包含的预测元素是预测编码层次结构的构建块。围绕减号的圆表示计算预测误差的误差单位向量；（b） 使 Rao-Ballard 协议更加清晰的数据流图。e^l 明确预测误差和水平。圆箭头表示减法。与预测元素关联的四个连接已标记

图 2. PE 预测单元。e 表示残差单元，r 表示表征单元，I 表示输入。黑色的小圆圈代表神经元。以实心圆结尾的红色箭头表示减法反馈抑制。红色箭头表示 P 连接，蓝色箭头表示 PE 连接，黑色箭头表示 LT 连接

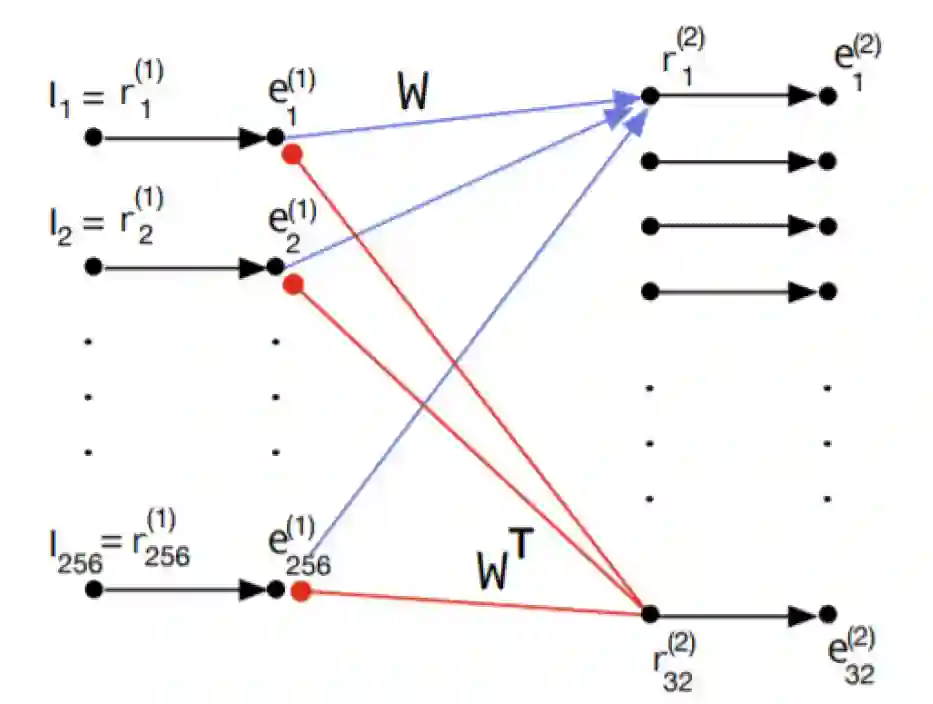
图 1（b）抛出了一个尚未有答案的问题：第 r^(l-1)层从第 r^(l+1)层中中获得了什么样的层次表示，这些层次表示与经典的深度学习模型（如卷积网络）中获得的层次表示相比如何？图 2 示出了 [5] 中模型第一层 PE 的网络级表示。为简单起见，假定第 2 层中的表示单元 r^(2)为线性。在接收层 r^(2)中，有两个表示 16x16 大小的图像块的输入像素强度的元素，但只有 32 个表示元素。前馈连接为蓝色 W，反馈连接为红色 W^T。自上而下的预测，表示为 I^。e^(1)单元计算预测误差。这些想法与架构处理有关：

根据公式 (1a)，I 是感官输入，第一层表征表示为 r^(1)，它们是等同的。I 和 I^ 的维度均为 256 x1（假设为 16 x 16 的输入图像块）。预测输入 I^ 也是等同于 r^(1)。预测输入表示为 W^Tr^(2)，其中 r^(2) 的维度为 32 x 1，W 的维度为 32 x 256。最后，在正常工作条件下，输入 I 和预测输入 I^ 应大致相等。公式 (1b) 将第 1 层的预测误差 e^(1)定义为实际输入和预测输入之间的差异。公式 (1c) 用于根据预测误差更新第二层的内部表征。从预测误差平方和的成本函数 J 开始。

考虑到仅针对单层网络，为了便于阅读，作者在公式中省略了层上标。在文献 [5] 中报告的成本函数包含了先验知识，但公式 (2) 的成本函数并未考虑先验知识。为了准备梯度下降，我们得到了 J 对 r 的导数。

对于梯度下降，我们以一定的速率沿导数的相反方向移动：

通过取 W^T 对 J 的导数，可得到如下所示的学习方程：

进一步的，给定图 2 中的模块，我们希望看到更大的体系结构是什么样子，以及当它嵌入到上下文层次结构中时会发生什么。为了实现这一点，图 3 扩展了图 2，在第一层中有两个横向 PE，在第二层中增加了一个 PE。层 2 的输入由三个重叠的 16x16 图像块组成。图 2 中的神经元 (r_1)^(1)-(r_1)^(32) 与图 3 中由 (r_1)^(1,2)-(r_1)^(32,2) 识别的神经元相同。新添加的第 3 层接收来自第 1 层的所有 PEs 的输入。在图 3 中，第一层的中间组件对应于图 2 中的模块。

图 3. 扩展后的文献 [5] 中模型的全局结构，显示了层次结构和相邻上下文。图 2 中的网络位于虚线框内

3、 PredNet: 用于视频预测和无监督学习的深度预测编码网络[3]

3.1 PredNet 介绍

文献 [4] 首次提出了深度预测编码网络（deep predictive coding networks）的概念，而文献 [3] 中提出的模型 PredNet，可能是使用深度学习（DL）框架实现的最早的预测编码模型。与上文描述的直接使用数学公式的方法相比，使用 DL 框架实现预测编码模型具有许多潜在优势。

• 首先，DL 框架非常成熟、通用且高效。因此，他们应该更容易建立和研究预测编码模型，唯一的复杂性是他们处理跨层反馈连接的能力。

• 其次，使用 DL 框架的模型可以扩展到具有超过十万个参数的非常大的体系结构。这不是使用传统的预测编码能够实现的。

• 第三，深度学习体系结构允许使用大型学习模块（如 LSTM），可以处理更宽松的统计假设，从而在更一般的情况下运行。

PredNet 属于第二类预测编码模型（如上文所述：像在泰勒级数展开中一样学习高阶误差的层次结构）。PredNet 的架构见图 4。PredNet 由一系列重复堆叠的模块组成，这些模块对输入进行局部预测，然后从实际输入中减去该预测并传递到下一层。具体的，每个模块由四个基本部分组成：输入卷积层（A_l）、递归表示层（R_l）、预测层（(a_l)^）和误差表示层（E_l）。R_l 是一个循环卷积网络，它生成 A_l 在下一帧上的预测(a_l)^。该网络获取 A_l 和(A_l)^ 之间的差值，并输出误差表示形式 E_l，包括单独的校正正误差总体和负误差总体。E_l 通过卷积层向前传递，成为下一层（A_l+1）的输入。R_l 接收 E_l 的副本以及来自下一级网络（R_l+1）的表示层的自顶向下的输入。网络的组织是这样的，在操作的第一个时间步骤中，网络的“右侧”（A_l’s 和 E_l’s）相当于标准的深度卷积网络。网络的 "左侧"（R_l’s）相当于一个生成性去卷积网络，每个阶段都有局部递归。与上一节介绍的经典预测编码模型不同，PredNet 构建为一个深度学习框架，它使用梯度下降法进行端到端的训练，同时隐式嵌入了一个损失函数作为误差神经元的触发频率。

图 4. PredNet 架构。左图：两层内信息流的图示。每一层由表示神经元（R_l）组成，表示神经元（R_l）在每个时间步（(a_l)^）输出特定于层的预测，并与目标（A_l）进行比较以产生误差项（E_l），然后误差项（E_l）在网络中横向和垂直传播

PredNet 架构适用于各种模拟数据，文献 [3] 具体关注图像序列（视频）数据。给定图像序列 x_t，下层的目标设置为实际序列本身，上层的目标则是通过对下层的误差单元进行卷积，然后通过 ReLU 和 Max pooling 处理得到的，使用 LSTM 作为表示神经元。(R_l)^t 利用 (R_l)^(t-1)、(E_l)^(t-1) 更新，以得到(R_l+1)^t。(A_l)^t^ 则通过(R_l)^t 堆的卷积附加 ReLU 处理得到。对于下层，(A_l)^t^ 通过一个设置为最大像素值饱和非线性集：

最后，(E_l)^t 计算为(A_l)^t^ 和(A_l)^t 的差，然后被分为 ReLU 激活的正预测误差和负预测误差，这些误差沿特征维度串联。完整的更新公式如下：

对模型进行训练以使误差单元活动的加权和最小。训练损失为：

对于由减法和 ReLU 激活组成的误差单元，每层的损失相当于 L1 误差。虽然本文没有针对此问题进行探讨，但作者表示也可以使用其他误差单元实现，甚至可能是概率的或对抗性的。完整的流程如下：

状态更新通过两个过程进行：一个自上而下的过程，其中计算(R_l)^t 状态，然后一个向前的过程，以计算预测、误差和更高级别的目标。最后一个值得注意的细节是 R_l 和 E_l 被初始化为零，这是由于网络的卷积性质，意味着初始预测在空间上是一致的。

3.2 PredNet 的预测编码分析

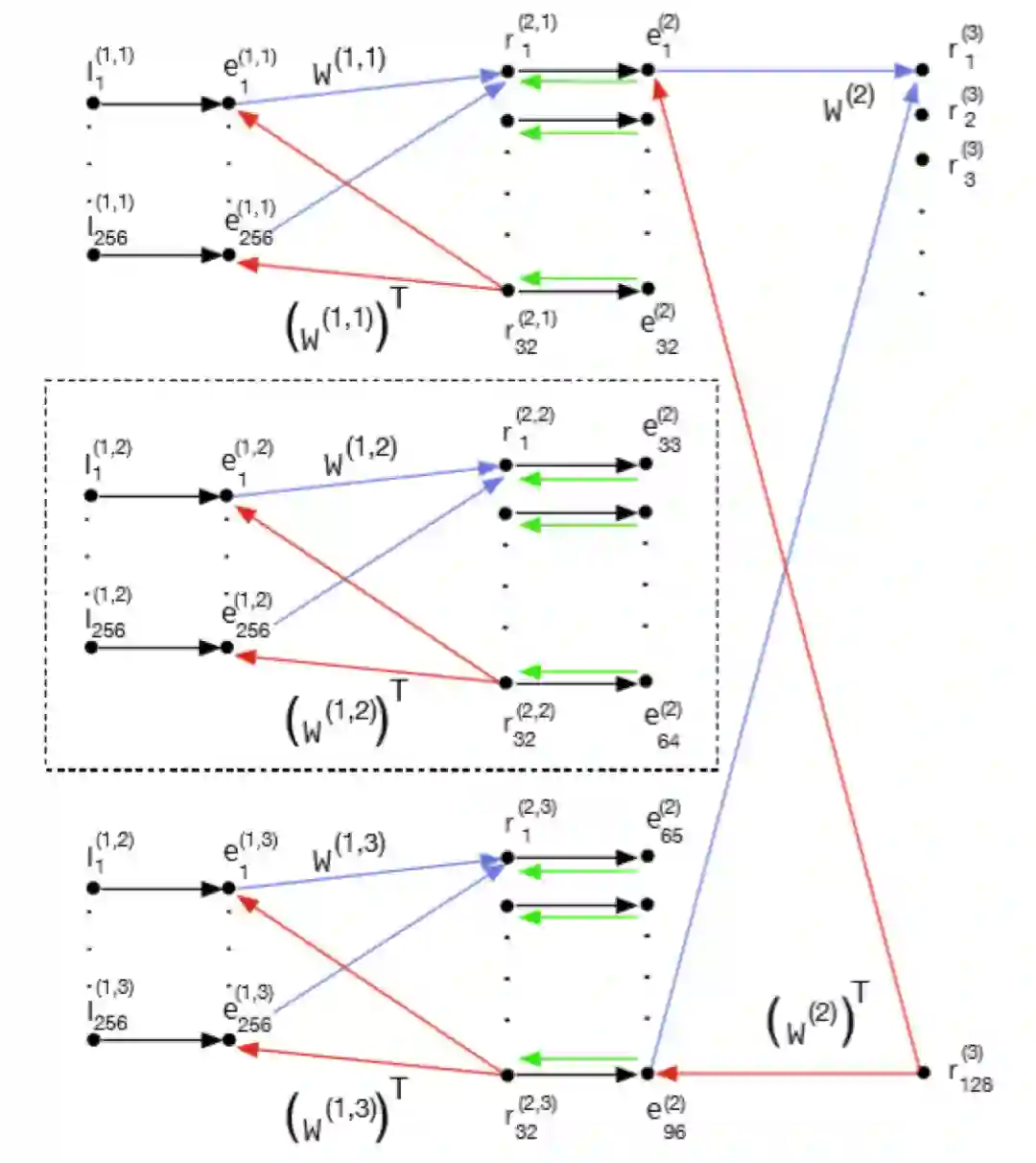
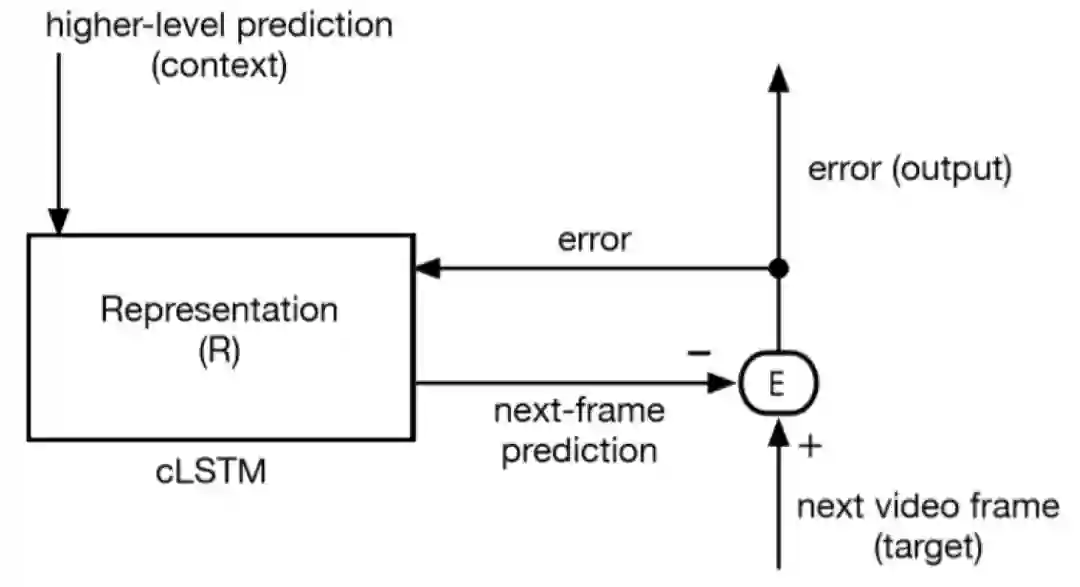
本小节介绍 PredNet 的图形化展示[1]。图 5 示出了模型最下层的 PredNet 预测元素（PE），其中左侧的表示模块实现为 cLSTM（convolutional LSTMs，卷积 LSTM）。由于 PredNet 处理视频数据，因此该模型中的表示模块由卷积 LSTM（cLSTMs）组成。cLSTM 是对 LSTM 的一种修改，它使用多通道图像作为其内部数据结构来代替特征向量。cLSTM 将基于仿射权乘（用于常规 LSTM）的门操作替换为适用于多通道图像的卷积门操作，以生成图像序列（如视频）的有用表示。表示模块的输出投射到误差计算模块，该模块将其输出发送回表示模块。该模型通过将预测结果与目标帧进行比较，并使用预测误差作为代价函数，来学习预测视频（目标）中的下一帧。由于图 5 没有显示前馈和反馈连接如何链接到下一个更上层，我们无法确定它是否是预测预测误差的模型。在这一点上，它作为预测编码模型是通用的。

图 5. PredNet 最下层（训练模式）中的信息流，其中输入为真实视频帧，R 和 E 是循环连接的

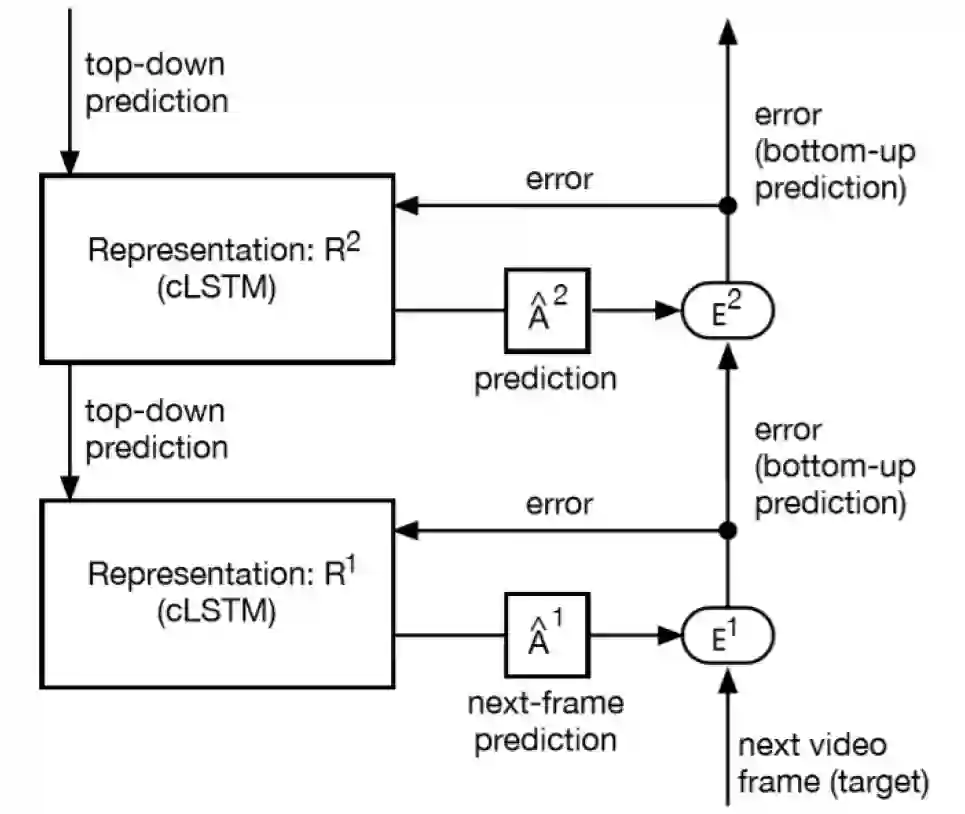
PredNet 与早期预测编码模型之间的根本区别在于 PredNet 中的模块间连接性与之前研究的模型不同。具体而言，PredNet 不遵循 RB 协议。这在图 5 中不容易看出，但在图 6（a）中很明显，图 6（a）给出了 PredNet 模型的两层版本，模块互连模式不同于 RB 协议。例如，PredNet 中第二层表示投影到第一层表示，而如果使用 RB 协议，它将投影到第一层误差。类似地，如果使用 RB 协议，第一层应投影到第二层表示。相反，PredNet 投影到了第二层误差。

下图6为PredNet 的两个视图。

（a）

（b）

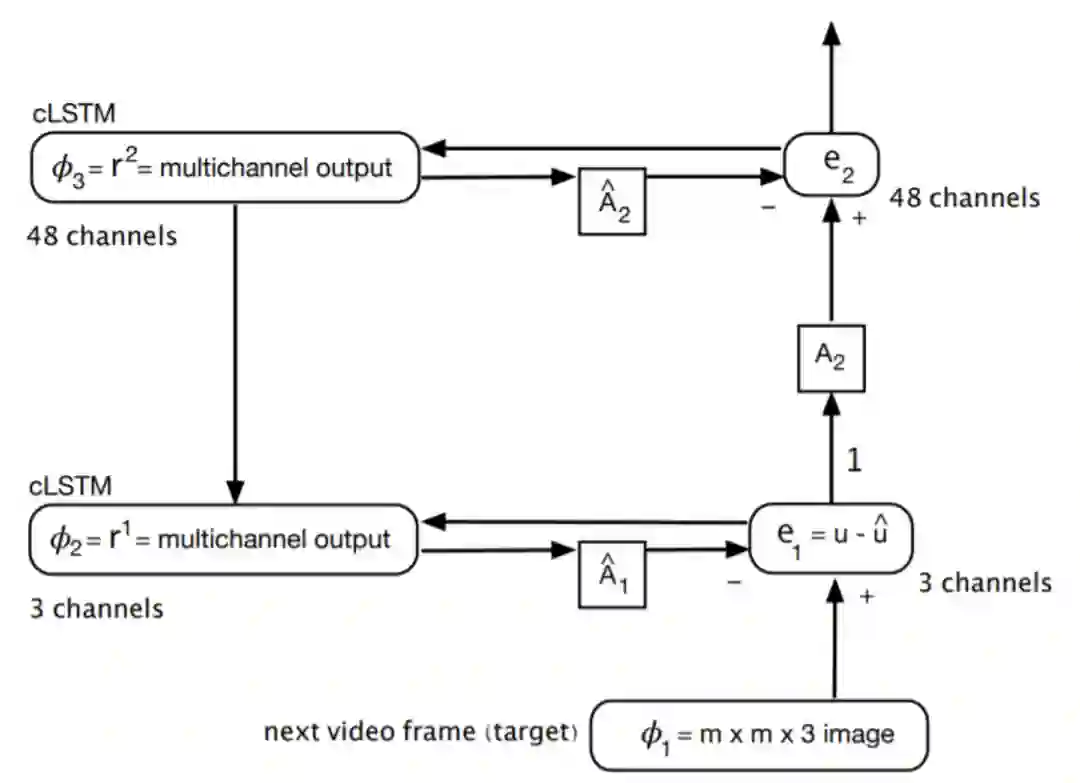
图6.PredNet的两个视图。（a） 简单的文字表述。（b） 重构图

我们可以通过图 6 具体分析 PredNet 的工作方法。当使用 L0 训练损失时，误差值 e2 不是训练损失函数的一部分，因此在第 2 层的表示中学习仅减少损失 e1。此外，两层的架构表示减少了高阶误差，但 L0 损失函数与此相反。因为 e2 并不影响训练。来自 e2 的反向传播权重更新信息沿箭头指向的相反方向流动。

假设：如果我们切断标记为 “1” 的连接，它对性能的影响应该可以忽略不计。如果这一假设被证明是正确的，那么更高级别的预测误差计算不会起到显著作用。Hosseini M 和 Maida A 认为，这意味着 PredNet 模型并非真正的预测编码网络，其功能原理类似于传统的深度网络。具体而言，它是一个分层 cLSTM 网络，在最下层使用平方误差损失之和[1]。虽然图 6 中没有明确显示，但在连续层之间的上行链路上使用了池化，在下行链路上使用了上采样。这实现了某种形式的分层空间上下文，但由于它将预测误差作为更上层次的表征，所以很难进行启发式解释。

4、利用 RB 协议对 PredNet 改进的思考[1]

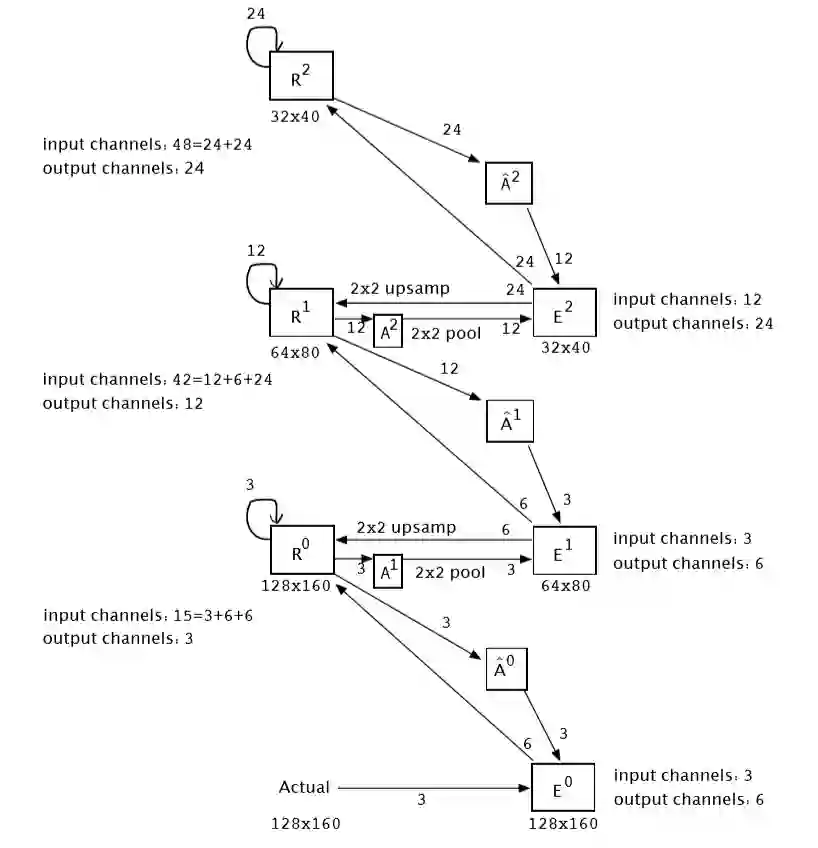
通过上文的介绍我们可以看出，PredNet 是第一个深度学习架构中的预测编码，但是它并不遵循 RB 协议。Hosseini M 和 Maida A 在 文献 [1] 中提出了一种利用 RB 协议改进 PredNet 的方法，命名为 RBP 模型（RB-PredNet），如图 7 所示。所有可训练参数都在 A^l、(A^l)^ 和 R^l 模块中。所有三种模块类型都执行多通道 2D 卷积运算。A^l 和(A^l)^ 模块使用一种操作，而 R^l 模块实现的是 cLSTM，因此一共使用了四组相同的操作。如果输出通道数为 oc，则需要 oc 多通道卷积来计算此输出，这是卷积集的大小。cLSTM 有三个门操作和一个输入更新操作，每个操作计算一个多通道卷积集。除了内核中的权重值外，这些集合是相同的。R^l 模块的输入通道数（表示为 ic）是前馈、横向和反馈输入的总和。所有卷积运算都使用平方滤波器，其内核大小在一维上由 k=3 表示。考虑到这些因素，下面的公式给出了一组多通道卷积的参数计数，称为卷积集：

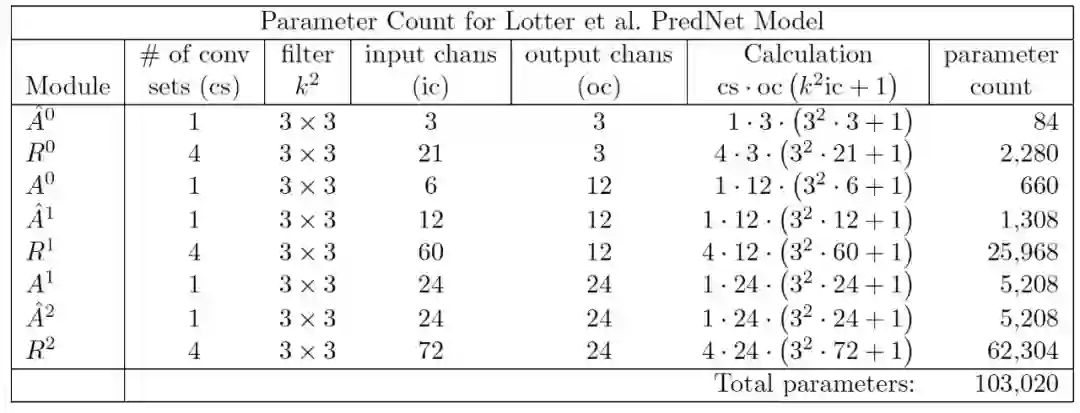
其中，括号中给出了多通道卷积滤波器的权重数。每个过滤器都有一个偏差。对于每个输出通道，需要一个多通道卷积。表 1 给出了图 7 中模型的参数计算量，该模型共有 65799 个可训练权重。

图 7. 改进的 RBP 模型架构

表 1. 图 7 所示模型的参数计算量。如果 R^l 模型中的 LSTM 被 GRU 替换，则参数计数为 50451，而不是 65799。这是通过将每个 R^l 模块中的卷积集的数量从四个更改为三个来实现的

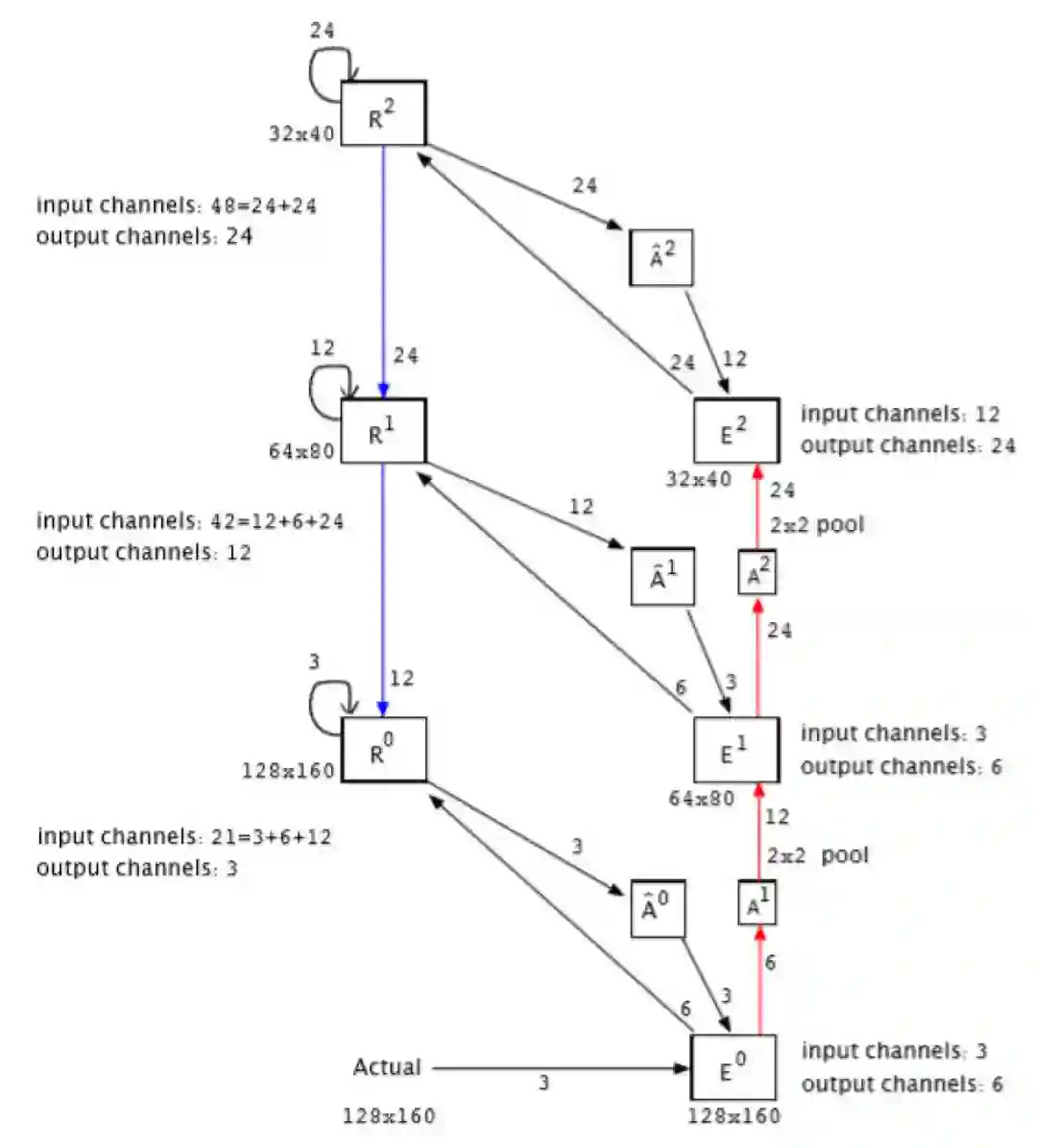
接下来，作者将图 7 中的 RBP 模型与原始 PredNet 3 层模型进行比较。两个模型都使用相同的 11 个模块。两种模式都被限制在 R^l 模块中使用相同的输出通道。为了将这些模块组合在一起，要求 Rl^ 模块的输入通道数不同，E^1 和 E^2 模块以及连接它们的 A^l 和(A^l)^ 模块的通道数也不同。由于输入通道的数量不同，图 8 模型有 103,020 个参数（参见表 2），而不是 65,799。图 7 和图 8 中连接模块的箭头表示信息流的方向。箭头上的数字标签表示该路径的通道数。每个模型的 R^l 模块中的输出通道数量是匹配的。

图 8. 扩充后的三层 PredNet 模型，其中，蓝色路线在 RBP 模型中不存在，但在扩充后的模型中使用，红色通路在 RBP 和混合模型中都是缺失的，这是原始 PredNet 模型特有的。箭头附近的标签是通道数。这种结构由表 3 中给出的 Pred1 和 Pred2 模型实现

表 2. 图 8 中涉及的参数计算量

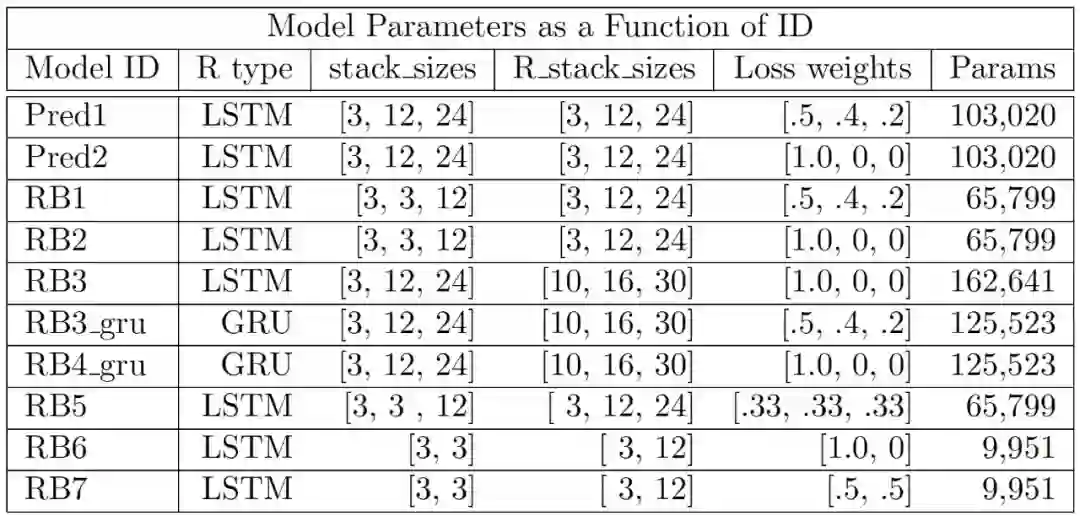
所有的模型都在预处理的 KITTI 交通数据集上使用 Adam 优化器训练了 20 个 epochs。该数据集经过预处理，以获得尺寸为 120 x 160 像素的三通道彩色图像。完成这个数据集上的预测任务需要模型检测和跟踪视频帧中的几个移动和非移动物体。作者通过实验测试了三种架构。第一个是 RBP 架构，其中 R^l 模块是由 cLSTMs 构建的。第二个也是 RBP 架构，其中 R^l 模块由卷积 GRU 构建。第三种是使用原始 PredNet 架构进行测试。如表 3 所示具体的模型体系结构规范。

表 3. 根据模型 ID 索引的模型体系结构规范。其中，"stack sizes" 是误差模块的输入通道数，"R stack sizes" 是表示模块的输出通道的数量，"Params" 是模型中可训练参数的数量

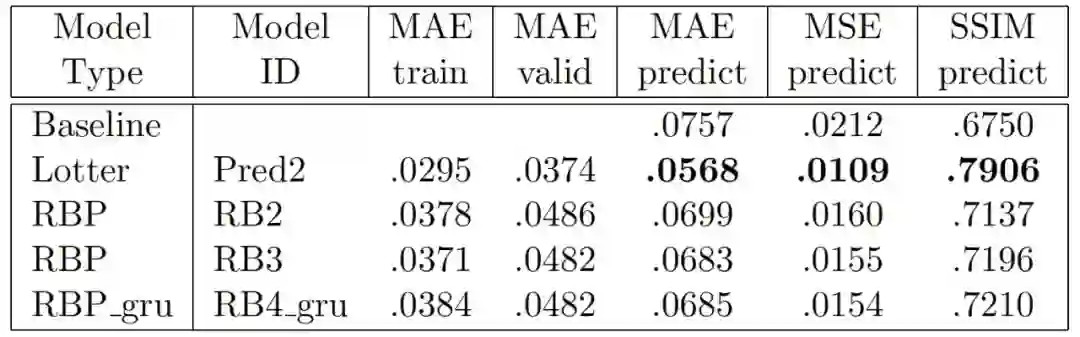
作者具体完成了两个实验。第一个实验使用的损失函数权重值为 [.5, .4, .2]。第二个实验使用的损失函数权重值为[1, 0, 0]。在所有的实验中，作者记录了三个性能指标：平均绝对误差（MAE）、平均平方误差（MSE）和结构相似度指数（SSIM）。所有指标都是在文献[3] 给出的基线控制条件下计算的，以便与神经网络性能指标进行比较。基线使用当前的视频帧作为下一帧的预测值。表 4 和表 5 分别给出两个实验的结果。作者将预测误差分数应与基线分数相比较。在训练阶段，RBP 模型对训练数据的平均绝对误差（MAE）为 .0191，对验证误差的平均绝对误差为 .0245。在测试阶段，MSE 下一帧的预测精度为 .0163，而使用前一帧作为预测的基线预测精度为 .0212。这些结果与 PredNet 模型非常接近。SSIM 的结果与 MAE 非常类似。这些结果表明，尽管这两个模型的通信结构不同，但实际上是等效的。第二个实验给出的结果与实验一有所不同。两个模型的预测性能都有所提高。就 Lotter 等人提出的 PredNet 模型而言，这是预料之中的，因为该结果已在原始论文中报告。

表 4. 使用 LSTM 的原始 PredNet 模型和使用 LSTM 和 GRU 的 RBP 模型的比较。两个模型的层损失函数权重都是[.5, .4, .2]。完整的模型规格可以通过查找表 3 中的模型 ID 找到。

表 5. 原始 PredNet 模型和 RBP 三层模型的比较。两个模型的损失函数权重都是[1.0, .0, .0]。关于模型的更多信息可以通过在表 3 中查询模型 ID 找到

5、小结

我们在这篇文章中对经典预测编码模型和深度学习架构中的预测编码模型进行了简单回顾。预测编码模型使用自上而下的重构机制来预测感觉输入或其低级别的表征，经典预测编码模型遵循 RB 协议。深度学习架构的 PredNet 构建了一个误差驱动的表征层次，其中， 上层表示的输入来自于前一层的预测误差，但 PredNet 并不满足 RB 协议。我们对文献 [1] 中提出的基于 RB 协议改进的 PredNet 也进行了介绍。由给出的实验结果分析可以，改进后的遵循 RB 协议的 RBP 模型确实提高了性能。

从定义的角度出发分析，我们可以看出预测编码模型的目的是 “减少预测误差”。不过，如果只是通过减少预测误差来生成表征，那么我们是无法保证这些获取的表征对特定的任务是有效的，例如分类任务。正如文献[1] 的作者在文章最后问到的，指导构建高阶表征的残余误差是如何提高 PredNet 模型的学习能力的？预测误差触发了学习，但是否还需要什么来触发特征层次的学习？

在我们撰写这篇文章的过程中对与预测编码相关的文献进行了搜索，与深度学习各类论文相比，预测编码相关的研究论文数量还非常有限。正如我们在上文中提到的，能够真正意义上称为深度学习架构中的预测编码的模型目前也就只有 PredNet 以及基于 PredNet 进行改进的一些版本。笔者猜测，这可能与预测编码 “仅致力于减少预测误差” 有关，在一些专门的任务中表现可能并不亮眼。但是，这种高度模拟大脑工作机制的方法 / 模型能否在实际场景中获得较好的应用效果，有待后续深入的研究和探索。

本文参考引用的文献：

[1] Hosseini M , Maida A . Hierarchical Predictive Coding Models in a Deep-Learning Framework[J]. 2020. https://arxiv.org/abs/2005.03230v1

[2] Huang Y , Rao R . Predictive coding[J]. Wiley Interdisciplinary Reviews Cognitive Science, 2011, 2(5):580-593. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.651.127&rep=rep1&type=pdf

[3] Lotter W , Kreiman G , D Cox. Deep Predictive Coding Networks for Video Prediction and Unsupervised Learning. ICLR 2017. https://arxiv.org/pdf/1605.08104.pdf

[4] Rakesh Chalasani and Jose C. Principe. Deep predictive coding networks. CoRR, 2013, http://export.arxiv.org/pdf/1301.3541

[5] Rao RPN, Ballard DH. Predictive coding in the visual cortex: a functional interpretation of some extraclassical receptive-field effects. Nat Neurosci 1999, 2: 79–87.

分析师介绍：

本文作者为Wu Jiying，工学博士，毕业于北京交通大学，曾分别于香港中文大学和香港科技大学担任助理研究员和研究助理，现从事电子政务领域信息化新技术研究工作。主要研究方向为模式识别、计算机视觉，爱好科研，希望能保持学习、不断进步。

关于机器之心全球分析师网络 Synced Global Analyst Network

机器之心全球分析师网络是由机器之心发起的全球性人工智能专业知识共享网络。在过去的四年里，已有数百名来自全球各地的 AI 领域专业学生学者、工程专家、业务专家，利用自己的学业工作之余的闲暇时间，通过线上分享、专栏解读、知识库构建、报告发布、评测及项目咨询等形式与全球 AI 社区共享自己的研究思路、工程经验及行业洞察等专业知识，并从中获得了自身的能力成长、经验积累及职业发展。

感兴趣加入机器之心全球分析师网络？点击阅读原文，提交申请。