量子态太「脆弱」如何纠错？MIT教授Peter Shor多年研究得到验证

2021 年 11 月 28 日 机器之心

选自quantamagazine

作者：Katie McCormick

机器之心编辑部

量子计算的一个目标就是以指数级倍数超过传统经典计算机的速度，但是在量子计算机中，量子比特比较脆弱，因为每个量子比特都处于 0 和 1 的混合状态，任何检测它们的方式都会直接破坏数据。来自 MIT 的应用数学系教授 Peter Shor 想出了一个方法，在不测量量子比特状态的情况下能够检测是否出现误差。

1994 年，任职于新泽西州贝尔实验室（Bell Labs）的数学家 Peter Shor 证实，量子计算机解决一些问题的速度较经典计算机呈现指数级的提升。但问题在于：这样的量子计算机能造出来吗？怀疑论者认为，量子态太「脆弱」了，环境将不可避免地混淆量子计算机中的信息，使其根本不成为量子。

Peter Shor

目前 Peter Shor 为 MIT 的应用数学系教授，于 2018 年获得了量子计算领域内的墨子量子奖（ Micius Quantum）。

经典纠错（error-correcting）方案测量单个比特来检查误差，但这种方法不适用于量子比特（qubits），这是因为任何测量都将破坏量子态及相应计算。Shor 想出了一个方法， 在不测量量子比特状态的情况下能够检测是否出现误差 。Shor 的相关工作标志着量子纠错领域的开始。

此后，量子纠错领域发展迅速，许多物理学家将其视为构建强大量子计算机的唯一途径。「如果没有量子纠错，我们将无法将量子计算机扩展到解决真正问题的程度，」加州理工学院的物理学家 John Preskill 说。

与一般的量子计算一样，开发纠错代码是一回事，在机器中实现是另一回事。但是在今年 10 月初，由马里兰大学物理学家 Chris Monroe 领导的研究小组报告说，他们已经证明了运行 Shor 那样的纠错电路所需的许多要素。

那么 Shor 是如何破解他面临的难题的呢？

不断的重复

Shor 根据经典中继器代码（repeater code）对协议进行建模，其中包括复制每一位信息，然后定期检查这些副本。如果其中一个位不同于其他位，计算机可以纠正错误并继续计算。

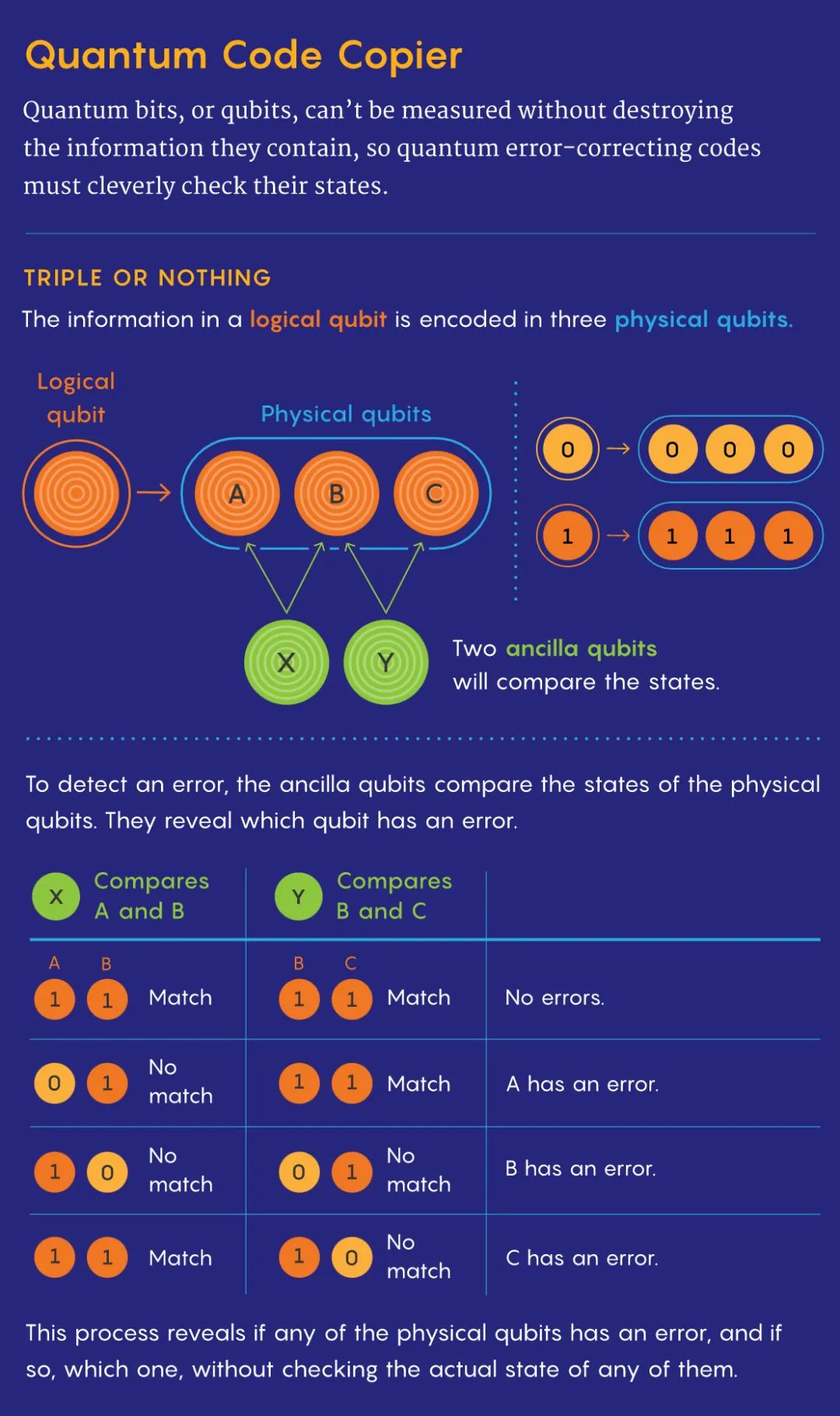
Shor 根据此设计了一个量子版本。他使用三个单独的物理比特来编码单个信息比特，即逻辑比特。Shor 的量子中继器代码和经典版本有所不同。量子计算的本质来自这样一个事实，即比特可以同时存在于 0 和 1 组合的叠加。由于测量量子态会破坏叠加，因此没有一种直接的方法来检查量子是否发生了错误。

庆幸的是，Shor 找到了一种方法可以判断量子的三个物理比特是否处于彼此相同的状态。他们发现如果其中一个比特不同，则表明发生了错误。

这项任务就像解决一个简单的逻辑难题。例如你有三个看起来相同的球，但其中一个球的重量可能不同。此外，你还有一个简单的天平。请问你采取哪种测量方法可以找出重量不同的球，如果有的话，是哪一个？

Samuel Velasco/量子杂志

答案是首先选择其中的两个球并比较它们的重量，然后用剩下的球替换其中一个并再次检查。如果天平两次都平衡，那么所有的球都是相同的。如果它只平衡过一次，那么其中一个被替换的球就是重量不同的球。如果两次天平都不平衡，则保持不动的球就是重量不一样的。

相同的道理，Shor 的代码用两个额外的「辅助」比特来进行比较。其中一个「辅助」比特比较第一个和第二个物理比特；另一个「辅助」比特比较第二和第三个物理比特。然后通过测量这些「辅助」比特的状态，你可以确定三个包含信息比特是否处于相同的状态，而不会干扰其中任何一个状态。

此代码还可以防止经典计算中的位翻转问题，但是比特还有一个潜在的错误来源，即「相」。

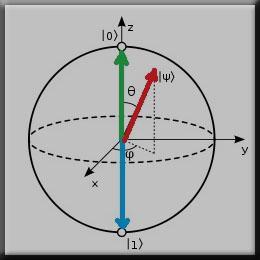
叠加是量子计算的关键，但是比特之间的相对「相」也很重要。你可以把「相」想象成一个波，它具有波峰和波谷位置。当两个波同相时，它们的波纹是同步的。如果它们相撞，它们会建设性干涉，合并成一个双倍大小的波。但是如果波是异相的，那么当一个波处于峰值时，另一个处于最低点，它们会相互抵消。

量子算法可以利用比特之间的这种相关系。该算法设置了这样一种情况，即计算的正确答案会产生建设性干涉并因此被放大，而错误答案会产生破坏性干涉并因此被抑制。

但是假如有一个错误导致相翻转，那么破坏性干涉就转换为建设性干涉，量子计算机将会放大错误答案。

Shor 发现可以纠正相错误，原理和比特翻转类似。每个逻辑比特都被编码为三个比特，并且辅助比特会检查其中一个相是否发生了翻转。

之后，Shor 将这两个代码进行组合。结果是一个代码将一个逻辑比特转换成九个物理比特，同时还提供位和相的检查。

容错

Shor 的代码原则上会保护单个逻辑比特免受错误影响。但是，如果误差测量本身存在错误怎么办？又或者当你在试图纠正不存在的错误时，就会不知不觉地引入一个真正的错误。在某些情况下，这会导致错误级联，然后传播到代码中。

因此，1996 年 Shor 提出了容错的概念。容错代码可以处理由环境、对比特不完美操作，甚至纠错步骤本身引入的错误——前提是这些错误的发生率低于某个阈值。

不久之前，Monroe 和他的团队宣布，他们使用了 Shor 的一个名为 Bacon-Shor 代码，以演示容错量子计算机所需的几乎所有工具。他们将一个逻辑比特编码为九个离子的量子态，外加四个辅助比特，他们表明他们可以容错地执行量子计算所需的所有单比特操作。结果表明，容错量子计算机是可能的。

不过，这个目标仍然遥不可及。Monroe 认为，在量子计算机达到 100 个逻辑比特之前，我们不会看到纠错带来的优势。具有纠错优势的机器大约需要 1,300 个物理比特，因为每个逻辑比特需要 9 个物理比特以及四个辅助比特（目前世界上最大的量子处理器为 IBM 新发布的 Eagle ，有 127 个物理比特）。「到那时，我们将开始制造一个量子比特工厂，引入纠错」Monroe 表示。

原文链接：

https://www.quantamagazine.org/how-quantum-computers-will-correct-their-errors-20211116/