ICLR 2022 | 微软亚洲研究院深度学习领域最新研究成果一览

（本文阅读时间：15分钟）

编者按：ICLR（International Conference on Learning Representations）是国际公认的深度学习领域顶级会议之一，众多在人工智能、统计和数据科学领域以及计算机视觉、语音识别、文本理解等重要应用领域极其有影响力的论文都发表在该大会上。今年的 ICLR 大会于4月25日至29日在线上举办。本届大会共接收论文1095篇，论文接收率32.3%。今天，我们精选了其中的六篇来为大家进行简要介绍，其中研究主题的关键词包括时间序列、策略优化、解耦表示学习、采样方法、强化学习等。欢迎感兴趣的读者阅读论文原文，一起了解深度学习领域的前沿进展！

01

周期性时间序列的深度展开学习

论文链接：https://www.microsoft.com/en-us/research/publication/depts-deep-expansion-learning-for-periodic-time-series-forecasting/

周期性时间序列在电力、交通、环境、医疗等领域中普遍存在，但是准确地捕捉这些时序信号的演化规律却很困难。一方面是因为观测到的时序信号往往对隐式的周期规律有着各种各样复杂的依赖关系，另一方面是由于这些隐式的周期规律通常也由不同频率、幅度的周期模式复合而成。然而，现有的深度时间序列预测模型要么忽视了对周期性的建模，要么依赖一些简单的假设（加性周期、乘性周期等），从而导致在相应预测任务中的表现不如人意。

在深入思考这些研究难点后，微软亚洲研究院的研究员们为周期性时间序列的预测问题提出了一套新型的深度展开学习框架 DEPTS。该框架既可以刻画多样化的周期性成分，也能捕捉复杂的周期性依赖关系。

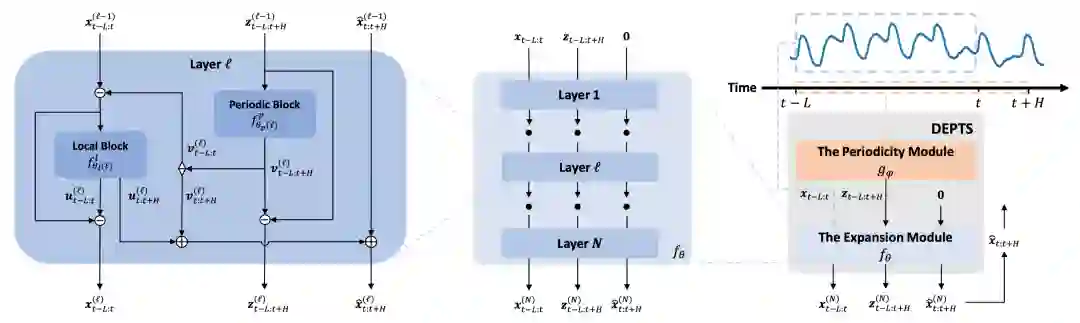
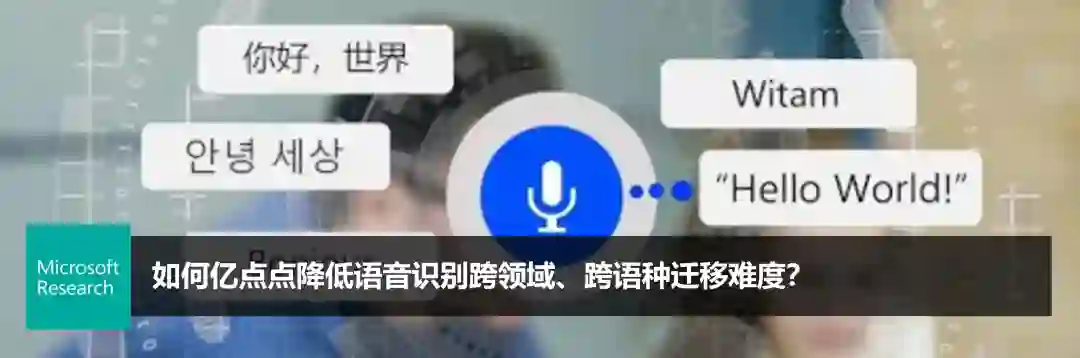
图1：DEPTS 框架图

如图1所示，DEPTS 主要包含两大模块：周期模块（The Periodicity Module）和展开模块（The Expansion Module）。首先，周期模块负责对整条时间序列的全局周期进行建模，接受全局时间作为输入，推断隐式的周期状态作为输出。为了有效刻画多种不同模式的复合周期，这里使用了一组参数化的周期函数（如余弦级数）来构建周期模块并使用相应变换（如离散余弦变换）来进行高效的参数初始化。

然后，基于一段观测的时间序列信号及其相应的隐式周期状态，展开模块负责捕捉观测信号与隐式周期之间复杂的依赖关系并做出预测。在这里，研究员们拓展了经典的深度残差学习思想开发了一种深度展开学习架构。在这个架构中，研究员们会对输入的时间序列及其隐式周期做逐层的依赖关系展开并得出相应预测分量。在每一层中，由参数化的周期神经网络来决定本层聚焦的周期分量，并展开观测信号的回看和预测分量。在进入下一层前，研究员们会减去本层中产生的周期分量和回看分量，从而鼓励后续的神经网络层聚焦于尚未展开的周期性依赖。按照这样的模式堆叠 N 层就构成了（深度）展开模块。

研究员们在生成数据和广泛的真实数据上都进行了实验验证，明确地揭示了现有方法在周期性时间序列预测方面的短板，并有力地证实了 DEPTS 框架的优越性。值得注意的是，在一些周期模式很强的数据上，DEPTS 相对已有最佳方案的提升可达20%。

此外，由于对周期性进行了明确的建模并提供了预测值在全局周期和局部波动两方面的分量展开，DEPTS 天生带有一定可解释性。

02

在基于模型的策略优化算法中，模型的梯度信息是重要的

论文链接：https://www.microsoft.com/en-us/research/publication/gradient-information-matters-in-policy-optimization-by-back-propagating-through-model/

基于模型的强化学习方法提供了一种通过与学到的环境进行交互从而获得最优策略的高效机制。在这篇论文中，研究员们研究了其中模型学习与模型使用不匹配的问题。具体来说，为了获得当前策略的更新方向，一个有效的方法就是利用模型的可微性去计算模型的导数。 然而，现在常用的方法都只是简单地将模型的学习看成是一个监督学习的任务，利用模型的预测误差去指导模型的学习，但是忽略了模型的梯度误差。简而言之，基于模型的强化学习算法往往需要准确的模型梯度，但是在学习阶段只减小了预测误差，因此就存在目标不一致的问题。

本篇论文中，研究员们首先在理论上证明了模型的梯度误差对于策略优化是至关重要的。由于策略梯度的偏差不仅受到模型预测误差的影响而且也受到模型梯度误差的影响，因此这些误差会最终影响到策略优化过程的收敛速率。

接下来，论文提出了一个双模型的方法去同时控制模型的预测和梯度误差。研究员们设计了两个不同的模型，并且在模型的学习和使用阶段分别让这两个模型承担了不同的角色。在模型学习阶段，研究员们设计了一个可行的方法去计算梯度误差并且用其去指导梯度模型的学习。在模型使用阶段，研究员们先利用预测模型去获得预测轨迹，再利用梯度模型去计算模型梯度。结合上述方法，本篇论文提出了基于方向导数投影的策略优化算法（DDPPO）。 最后，在一系列连续控制基准任务上的实验结果证明了论文中提出的算法确实有着更高的样本效率。

图2： (a)模型学习和使用中的不一致。 (b)DDPPO 算法的示意图。DDPPO 算法分别构造了预测模型和梯度模型。DDPPO 算法使用不同的损失函数去分别训练这两个模型，并且在策略优化中分别恰当地使用他们。

03

RecurD递归解耦网络

论文链接：https://www.microsoft.com/en-us/research/publication/recursive-disentanglement-network/

机器学习的最新进展表明，解耦表示的学习能力有利于模型实现高效的数据利用。其中 BETA-VAE 及其变体是解耦表示学习中应用最为广泛的一类方法。这类工作引入了多种不同的归纳偏差作为正则化项，并将它们直接应用于隐变量空间，旨在平衡解耦表示的信息量及其独立性约束之间的关系。然而，深度模型的特征空间具有天然的组合结构，即每个复杂特征都是原始特征的组合。仅将解耦正则化项应用于隐变量空间无法有效地在组合特征空间中传播解耦表示的约束。

本篇论文旨在结合组合特征空间的特点来解决解耦表示学习问题。首先，论文从信息论的角度定义了解耦表示的属性，从而引入了一个新的学习目标，包括三个基本属性：充分性、最小充分性和解耦性。从理论分析表明，本篇论文所提出的学习目标是 BETA-VAE 及其几个变种的一般形式。接下来，研究员们将所提出的学习目标扩展到了组合特征空间，以涵盖组合特征空间中的解缠结表示学习问题，包括组合最小充分性和组合解耦性。

基于组合解耦学习目标，本篇论文提出了对应的递归解缠结网络（Recursive disentanglement network, RecurD），在模型网络中的组合特征空间内，递归地传播解耦归纳偏置来指导解缠结学习过程。通过前馈网络，递归的传播强归纳偏差是解耦表示学习的充分条件。实验表明，相较于 BETA-VAE 及其变种模型，RecurD 实现了更好的解耦表示学习。并且，在下游分类任务中，RecurD 也表现出了一定的有效利用数据的能力。

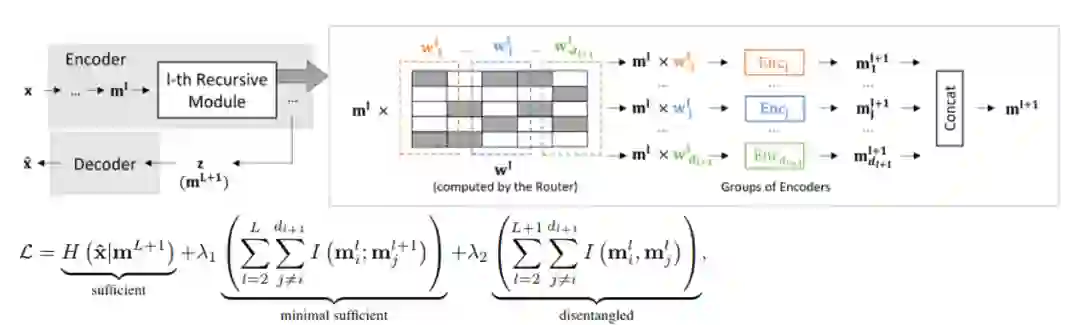
图3：RecurD 网络结构

04

基于镜像斯坦因算符的采样方法

论文链接：https://www.microsoft.com/en-us/research/publication/sampling-with-mirrored-stein-operators/

贝叶斯推理（Bayesian inference）等一些机器学习及科学计算问题都可归结为用一组样本来代表一个只知道未归一化密度函数的分布。不同于经典的马尔可夫链蒙特卡罗（Markov chain Monte Carlo）方法，近年来发展起来的斯坦因变分梯度下降方法（Stein variational gradient descent，简记为 SVGD）具有更好的样本高效性，但对在受限空间（图中Θ）上分布的采样或对形状扭曲的分布的采样仍显吃力。

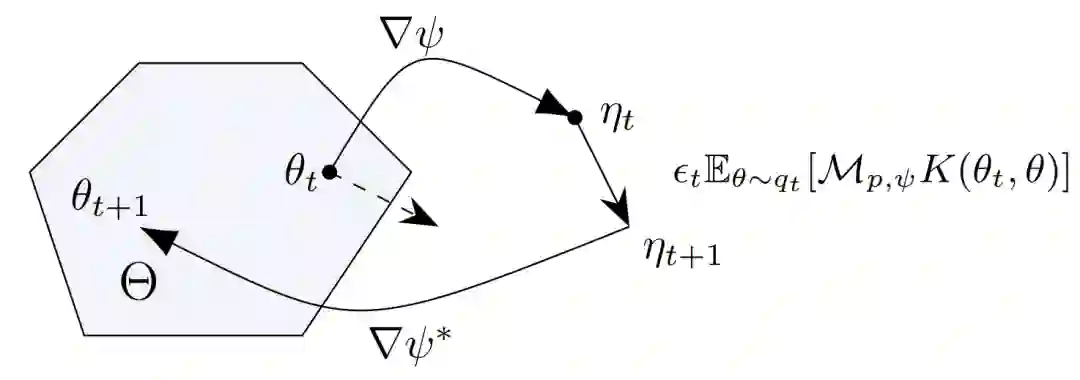
图4：原样本空间\Theta及其镜像空间示意

本篇论文中，研究员们借鉴优化领域中镜像下降方法（mirrored descent）的思想，推导设计出了一系列镜像斯坦因算符（mirrored Stein operators）及其对应的镜像 SVGD 方法。原空间经镜像映射（图中∇ψ）所得的镜像空间是不受限的并可体现分布的几何信息，因而这些方法系统性地解决了上述问题。

具体来说，SVGD 的原理是使用能最大化样本分布与目标分布之间 KL 散度减小率的更新方向来更新样本，从而使样本分布不断逼近目标分布，而这个减小率和更新方向都是由斯坦因算符给出的。因而论文首先推导出了镜像空间中的斯坦因算符（图中 M_(p,ψ)）和样本的更新方向（图中 E_(θ∼q_t ) [M_(p,ψ) K(θ_t,θ)]）。

研究员们进而设计了三种计算更新方向所需的核函数（kernel function，图中 K），分别可在单样本情况下划归为针对镜像空间及原空间上目标分布峰值的梯度下降，以及原空间上的自然梯度下降。该论文还推导了所提方法的收敛性保证。实验发现所提方法比原本的 SVGD 有更好的收敛速度和精度。

05

部署高效的强化学习：理论下界与最优算法

论文链接：https://www.microsoft.com/en-us/research/publication/towards-deployment-efficient-reinforcement-learning-lower-bound-and-optimality/

传统的（在线）强化学习（RL）的学习过程可以概括为两部分的循环：其一是根据收集的数据学习一个策略（policy）；其二是将策略部署到环境中进行交互，获得新的数据用于接下来的学习。强化学习的目标就是在这样的循环中完成对环境的探索，提升策略直至最优。

然而在一些实际应用中，部署策略的过程会十分繁琐，而相对来讲，当部署完新的策略之后，数据的收集过程是很快的。比如在推荐系统中，策略就是推荐方案，好的策略可以精准地推送用户所需要的内容。考虑到用户体验，通常一家公司在上线新的推荐策略之前会进行很长时间的内部测试来检验性能，由于庞大的用户基数，往往部署之后短时间内就可以收集到海量的用户反馈数据来进行后续的策略学习。在这样的应用中，研究员们更倾向于选择只需要很少部署次数（deployment complexity）就能学到好策略的算法。

但是现有的强化学习算法以及理论和上述真实需求之间还有距离。在这篇论文中，研究员们尝试去填补这个空白。研究员们首先从理论的角度上，对 deployment-efficient RL 这个问题提供了一个比较严谨的定义。之后以 episodic linear MDP 作为一个具体的设定，研究员们分别研究了最优的算法能表现的怎样（lower bound），以及提出了可以达到最优的部署复杂度的算法设计方案（optimality）。

其中，在 lower bound 部分，研究员们贡献了理论下界的构造与相关证明；在 upper bound 部分，研究员们提出了“逐层推进”的探索策略（如图5所示），并贡献了基于协方差矩阵估计的新的算法框架，以及一些技术层面的创新。研究员们的结论也揭示了部署带有随机性的策略对于降低部署复杂度的显著作用，这一点在之前的工作当中往往被忽略了。

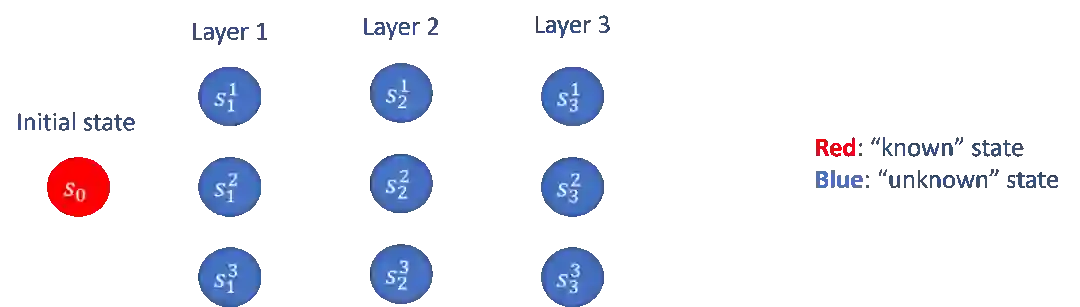
图5：“逐层推进”的探索策略（以3层的离散马尔科夫决策过程为例）

06

强化学习中的变分先知引导

论文链接：https://www.microsoft.com/en-us/research/publication/variational-oracle-guiding-for-reinforcement-learning/

GitHub链接：https://github.com/Agony5757/mahjong

深度强化学习（DRL）最近在各种决策问题上都取得了成功，然而有一个重要的方面还没有被充分探索——如何利用 oracle observation（决策时不可见，但事后可知的信息）来帮助训练。例如，人类扑克高手会在赛后查看比赛的回放，在回放中，他们可以分析对手的手牌，从而帮助他们更好地反思比赛中自己根据可见信息（executor observation）来做的决策是否可以改进。这样的问题被称为 oracle guiding。

在这项工作中，研究员们基于贝叶斯理论对 oracle guiding 的问题进行了研究。本篇论文提出了一种新的基于变分贝叶斯方法（variational Bayes）的强化学习的目标函数，来利用 oracle observation 帮助训练。这项工作的主要贡献是提出了一个通用的强化学习框架，称为 Variational Latent Oracle Guiding (VLOG)。VLOG 具有许多优异的性质，比如在各种任务上都有着良好且鲁棒的表现，而且 VLOG 可以与任何 value-based 的 DRL 算法相结合使用。

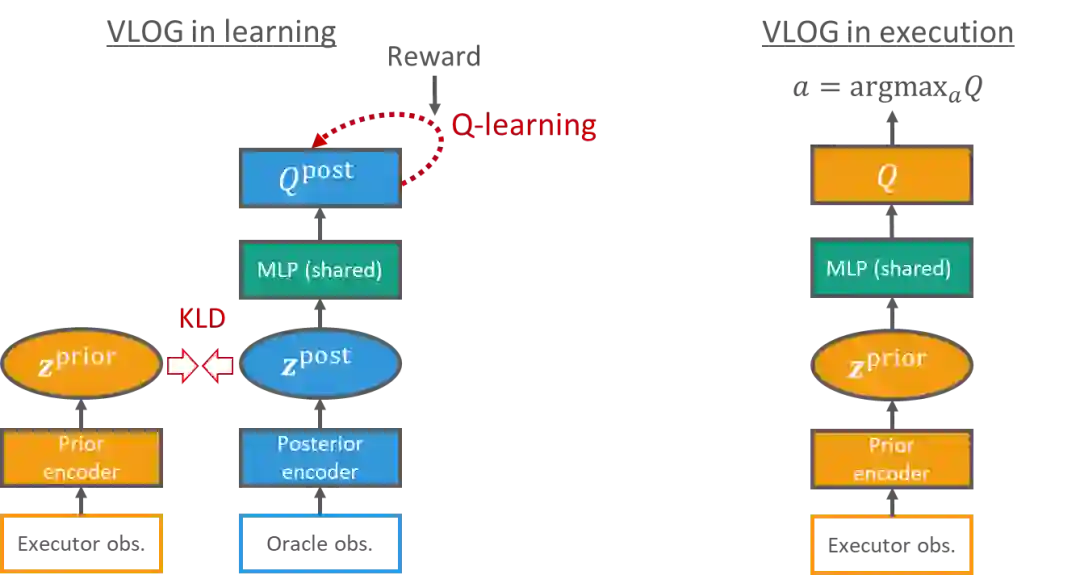
图6：VLOG 在训练时和使用时的模型图表（以 Q-learning 为例）。左：训练时（知道 oracle observation），分别用 executor observation 和 oracle observation 来估计一个贝叶斯隐变量z的先验（prior）和后验（posterior）分布。通过优化 VLOG 变分下界（variational lower bound，后验模型的强化学习目标函数减去z的后验和先验分布之间的KL散度）来训练整个模型。右：使用时，基于可见信息来做出决策。

研究员们对 VLOG 进行了各种任务的实验，包括一个迷宫，简明版的 Atari Games，以及麻将。实验涵盖了在线以及离线强化学习的不同情况，均验证了 VLOG 的良好表现。 此外，研究员们还开源了文中使用的麻将强化学习环境和对应的离线强化学习数据集，来作为未来 oracle guiding 问题和复杂决策环境研究的标准化测试环境 。

你也许还想看：