我们必须知道, 我们必将知道
Gauss
我们必须知道, 我们必将知道
陈关荣 | 文
Dirichlet
Riemann
Felix Klein
开 篇
已获陈关荣教授授权[遇见数学]发布此文, 特此感谢!

陈关荣 CHEN GUAN RONG
陈教授1981年获广州中山大学计算数学硕士学位, 1987年获美国Texas A&M大学应用数学博士学位, 后在美国Rice和Houston大学任教. 2000年起, 香港城市大学讲座教授职位工作至今.
Wir müssen wissen, wir werden wissen(我们必须知道,我们必将知道)——这是大卫·希尔伯特 1930 年退休感言的结束语,镌刻在哥廷根城市墓地(Stadtfriedhof Gӧttingen)里他那简单墓碑的下方。

△2015 年 9 月 10 日,本文作者在哥廷根参拜希尔伯特墓地
大卫·希尔伯特(David Hilbert, 1862-1943)出生于东普鲁士的哥尼斯堡(Kӧnigsberg)附近。 哥尼斯堡是哲学家康德的故乡,也是欧拉研究七桥问题和数学家雅可比任教的地方,现在归属俄罗斯。1880 年,希尔伯特违背了父亲让他读法律的意愿而进入哥尼斯堡大学学习数学,师从林德曼(Carl von Lindemann,1852-1939),22 岁获得博士学位。之后留校任教,31 岁晋升正 教授。1895 年,希尔伯特转入哥廷根大学(全称是 Georg-August-Universität Göttingen)任职 教授,在那里度过了余生,于 1943 年辞世。他曾获俄罗斯罗巴切夫斯基奖和瑞典科学院 Mittag-Leffler 奖,1942 年当选为柏林科学院荣誉院士。

△ David Hilbert (1862-1943)
希尔伯特是历史上最卓越的数学家之一,在不变量理论、代数数论、积分方程、变分法、泛函分析、数学和几何学基础、数学物理等领域中作出了十分重要的贡献。今天,“希尔伯特空间”、 “希尔伯特变换”、“希尔伯特矩阵”、“希尔伯特曲线”等冠以其名的术语和他那有趣的“希尔伯特旅馆悖论”均广为人知。
注:希尔伯特旅馆悖论可参看此文 - 【希尔伯特旅馆悖论】
1900 年,38 岁的希尔伯特在巴黎举行的第二届国际数学会议上以“数学问题”为题的演讲中提出了 23 个重要的数学难题,即众所周知的“希尔伯特问题”,激励和推动了后来一个多世纪许多数学分支的蓬勃发展。简而言之,希尔伯特的第 1 - 6 问题关于数学基础理论,第 7 - 12 问题关于数论,第 13 - 18 问题属于代数和几何,而最后的第 19-23 问题属于数学分析范畴。经过许多 数学家长期的努力,目前大多数问题都得到了完全或部分解答。鉴于他本人的研究兴趣和当时的历史条件,希尔伯特问题中未能包括拓扑和微分几何等重要领域的数学问题,也基本上没有涉及应用数学和计算数学。当然,没有人会苛求希尔伯特用 23 个问题去涵盖浩瀚的数学分支和内容。实际上,二十世纪数学的发展远远超出了希尔伯特当时的设想。
希尔伯特的第二问题是有名的“判定问题”,它至关重要,涉及整个数学基础,关心数学是否完备和一致?是不是所有数学命题都可以通过有限次正确的数学步骤作出判定?希尔伯特雄心勃勃,要将整个数学体系严格公理化,然后用他的所谓“元数学”(证明数学的数学)来证明整个数学体系是坚不可摧的。为了这个目标,他制定了一个后人称之为“希尔伯特计划”的部署:首先,将所有数学形式化,把每一个数学陈述都用符号来表达。然后,证明整个数学系统是完备的,即对任何一个数学陈述都存在一个数学证明。同时,还要证明数学是一致的,也就是说绝不存在自相矛盾的陈述。最后,还要有一个可以实现的算法,通过有限步程序最终判定数学陈述的对错。显然,这是一个野心勃勃的宏图大计,但希尔伯特并不认为它是不可能的。 他非常自信,断言“不存在不可解的问题”。
遗憾的是,“希尔伯特计划”在他 1930 年光荣引退后随即惨遭失败。1930 年 9 月 7 日,时年 25 岁的哥德尔(Kurt Friedrich Gödel,1906-1978)发表了著名的“不完备性定理”:“如果数学是一致的,那么它就是不完备的”。具体地说,哥德尔证明了:任何一个包含算术系统在内的数学系统不可能同时是完备的和一致的。换句话说,人们如果能在一个数学系统中做算术的话,那么这个系统或者是自相矛盾的,或者存在一些结论在这个系统内是无法证明的。其次, 他证明了,对于任意一个包含算术系统的数学系统来说,不可能在这个系统内部证明它本身的一致性。哥德尔的结论对当时整个数学界来说无疑是一次颠覆性的冲击。希尔伯特别无选择, 旋即对计划作了修正,取消了有限步骤这个约束。随后,根茨(G. Gentaen,1909-1945)于 1936 年使用某种非形式化方法(超限归纳法)证明了算术公理系统的一致性。虽然这一切与希尔伯特的初衷有别,但是他的元数学、形式化和证明论的基本思想依然深刻地影响了许多后世数学家。
谈论希尔伯特不能不提及哥廷根大学和哥廷根数学学派。
哥廷根大学属于德国,却是由英王乔治二世于 1734 年创立的,初期以法学闻名于世,被称为 “法科大学”,培养出许多杰出的政治家、哲学家、语言学家和教育家,如奥地利首相克莱门 斯·梅特涅(Klemens von Metternich,1773-1859)、柏林大学创立者威廉·洪堡(Wilhelm von Humboldt,1767-1835)、大诗人海因里希·海涅(Christian Heine,1797-1856)、文学巨匠格林兄弟(Jacob Grimm, 1785-1863 和 Wilhelm Grimm, 1786-1859)、哲学家亚瑟·叔本华(Arthur Schopenhauer,1788-1860)以及社会学家马克斯·韦伯(Max Weber,1864- 1920)和尤尔根·哈贝马斯(Jürgen Habermas,1929-)等。此外,德意志帝国“铁血宰相” 奥托 · 俾 斯 麦 ( Otto von Bismarck , 1815-1898 ) 也 是 该 校毕 业生。法国 统 帅 拿 破 仑(Napoléon Bonaparte,1769-1821)曾在此研习法律,说“哥廷根是属于全欧洲的。” 哥廷根大学著名校友中还有中国的国学大师季羡林,他 1937 年在该校求学时兼任汉学系讲师,于1941 年获博士学位。
除了法学和哲学之外,哥廷根大学更是世人瞩目的自然科学和文化中心,以倡导学术自由和独创风格闻名于世。这种学风和治学精神使它一度成为培育世界级科学巨匠的摇篮,先后有 47 位 诺贝尔奖得主在此读书毕业、秉职任教或长期访研,主要为物理和化学奖,并有一些医学、和平以及文学奖。最近获得诺贝尔奖的有 2013 年生理学奖得主 Thomas C. Südhof(1982 年哥廷 根大学神经化学博士)和 2014 年的化学奖得主 Stefan W. Hell(时任哥廷根普朗克生物物理化 学研究所主任)。
回顾哥廷根大学二百八十多年的历史,可知她在十九和二十世纪达到鼎盛,出现过电磁学家威 廉·韦伯(Wilhelm Eduard Weber,1804-1891)和原子弹之父罗伯特·奥本海默(Julius Robert Oppenheimer,1904-1967),以及二十多个物理诺贝尔奖和十多个化学诺贝尔奖得主 的教员和学生,包括熟知的赫兹(Heinrich Hertz,1857-1894)、普朗克(Max Planck, 1858-1947)、哈恩( Otto Hahn, 1879-1968 )、 玻恩(Max Born, 1882-1970)、德拜(Peter Debye , 1884-1966)、 泡利(Wolfgang Pauli ,1900-1958)、 海森堡(Werner Heisenberg,1901-1976)和费米(Enrico Fermi, 1901-1954)。哥廷根大学的数学成就同样 灿耀无比,在那里群星荟萃,出现过许多数学大师,包括高斯(Carl Friedrich Gauss,1777-1855)、狄利克雷( Johann Dirichlet, 1805-1859) 、 黎 曼 (Bernhard Riemann, 1826-1866)、戴德金(Julius Wilhelm Dedekind, 1831-1916)、克莱布什(Alfred Clebsch, 1833-1872 )、韦伯(Heinrich Weber, 1842-1913)、 许瓦兹( Hermann Schwarz ,1843- 1921)、克莱因(Felix Klein,1849-1925)、柯瓦列夫斯卡娅(Sofia Kovalevskaya,1850-1891)、希尔伯特(David Hilbert,1862-1943)、闵可夫斯基(Hermann Minkowski,1864-1909)、诺特(Emmy Noether,1882-1935),以及希尔伯特的学生外尔(Hermann Weyl,1885-1955)和柯朗(Richard Courant,1888-1972)。在数学史上,哥廷根大学的数学有过两大辉煌时期——高斯时期(十九世纪)和克莱因-希尔伯特时期(二十世纪)。
注:文末有[遇见数学] 设计《哥廷根数学天空的闪烁群星》海报图片
高斯被认为是历史上最重要的数学家之一,享有“数学王子”的盛誉。他出生于平民家庭,父 亲一生做杂工,母亲没有文化。高斯自幼聪颖好学,他 10 岁时巧妙地算出级数 1 + … + 100 求和的故事家喻户晓。高斯 22 岁获博士学位,在博士论文中给出了代数基本定理的第一个严格证明 (他后来还给出另外三个证法,其中最后一个是他 71 岁时公布的)。他 25 岁当选圣彼 德堡科学院外籍院士、30 岁出任哥廷根大学数学教授。人们对他用圆规直尺作圆内接正十七边形特别是最小二乘法和正态分布耳熟能详。他的数学贡献涵盖数论、代数、统计、分析、微分 几何、复变函数、矩阵理论等许多方面,并曾对非欧几何有过创始性的研究。高斯的内蕴曲面几何学思想启发了他的学生黎曼发展出高维空间的一般内蕴几何学,后来成为爱因斯坦广义相对论的数学基础。爱因斯坦曾说:“高斯对于近代物理学的发展,尤其是对于相对论的数学基础所作的贡献,其重要性是超越一切、无与伦比的。”
高斯同时又是一个物理学家和天文学家,一生成就极为丰硕,对数学、力学、天文学、电磁学、 大地测量学、地球物理学以至光学都有卓越贡献,以他名字命名的成果有一百多个。高斯和威廉·韦伯一起从事磁学研究(因而产生了磁通密度单位:1 韦伯/平方公尺 = 10000 高斯)、画 出了世界上第一张地球磁场图并确定了地球磁南北极位置,并一起设计了前所未有的有线电报 机。高斯还凭借数学计算准确地预测了谷神星(Ceres)的存在并由此启导了智神星(Pallas) 以及其他一些行星的发现,之后兼任过哥廷根大学天文学教授和天文台台长。高斯毕生在哥廷根大学任教,直至 77 岁时于睡梦中安然辞世。高斯的第一教授位置先后由狄利克雷和黎曼接任。
高斯一生衣食简朴、深居简出。据说他只参加过一次学术会议,就是 1828 年柏林自然科学工作者大会。他不涉足政治,不参与公开争论,对关于自己的流言蜚语也不正式辩解,即使在 1837 年 11 月 18 日著名的“哥廷根七君子”(Göttinger Sieben)事件中,当包括语言学家格林兄弟、 高斯的长 期合 作者 物理 学家 威廉 · 韦伯以及 高 斯自己的女婿东方学家埃瓦尔德(G.H.A.von Ewald)等七位著名学者因抗议国王废除宪法而被集体解职时,高斯也保持缄默。高斯是个完美主义者,一般不发表未成熟和自觉价值不高的论著。他培养的博士学生不 多,但却有高足黎曼、戴德金、莫比乌斯(August Möbius)和贝塞尔(Friedrich Bessel)。由于高斯自身的勤奋努力和极高水平的学术贡献,他在哥廷根引领出一个数学学派。他本人的数学文汇《高斯全集》(Carl Friedrich Gauss Werke) 共 12 卷,由众多著名数学家参与编辑,其出版历时六十多年(1863-1929),在克莱因统筹主导下完成。
值得一提的是高斯的学生黎曼,在学术上完全秉承了导师严谨的治学风格。黎曼只有短短的四十年人生,正式发表的论文不多,可是他的名字却频繁地出现在后来的数学文献里,诸如黎曼积分、黎曼引理、黎曼映照定理、黎曼-希尔伯特问题、柯西-黎曼方程、黎曼思路回环矩阵、 黎曼曲面、黎曼流形、黎曼空间,特别是迷人的黎曼 zeta 函数。黎曼留给后人的最大难题是著名的“黎曼猜想”,即希尔伯特 23 个问题中的第 8 问题,它要求回答黎曼 zeta 函数的非平凡零点是否全部位于复平面实部为 1/2 的直线上?这是一个至今悬而未决的最重要的数学问题之 一。据说希尔伯特老年时曾被人问到:“假定你去世后有一天能够复活,那么您会去做什么呢?”希尔伯特毫不迟疑地回答:“我会首先去打听黎曼猜想解决了没有。”

△ 本文作者是高斯第十代博士学生:
Gauss-Bessel-Scherk-Kummer-Schwarz-
-Fejer-Polya-Edrei-Hellerstein-Chui-Chen
高斯之后,克莱因引领出了哥廷根数学学派的第二个强盛时期,即克莱因-希尔伯特时期。
克莱因在 1871 年服完兵役后来到哥廷根大学出任数学讲师,开始了他的学术生涯。次年,23 岁的他便被埃尔朗根(Erlangen)大学聘为数学教授。之后,他曾在慕尼黑高等技术学院和莱比锡大学任教。克莱因 1886 年回到哥廷根大学并在那里工作至 1913 年 64 岁退休。1872-1895 年间克莱因任《哥廷根数学年刊》主编,期间还编辑了《数学百科全书》并亲自编写了第 4 卷。 克莱因 1885 年被英国皇家学会选为外籍院士,1908 年担任在罗马召开的国际数学家大会主席, 1913 年被选为利奥波第那科学院(Deutsche Akademie der Naturforscher Leopoldina,即今天的德国科学院)院士。
克莱因最广为人知的是他的“克莱因瓶”,概念上和“莫比乌斯带”类似,简单有趣,引人入胜。克莱因最出名的是他 1872 年在埃尔朗根大学哲学系和大学理事会上所做的题为“关于近代几何研究的比较考察”的演讲,被后人称为“埃尔朗根纲领”,论证了如何把多种几何(黎曼几何除外)统一在变换群论观点之下。
克莱因具有非凡卓越的组织和领导能力。他最成功的是组织并带领了哥廷根数学学派乃至整个哥廷根大学自然科学学派在世界学术原野上异峰突起。1893 年,克莱因从芝加哥世界博览会回国后,有感于美国理论研究在工业应用上的成功,开始倡导理论与实践相结合,引导哥廷根大学的自然科学突破纯科学与实际运用之间的界线,以适应科学繁荣与工业化时代的需求,竭力促进数学、力学和其他基础学科在工程技术中的应用,并在哥廷根大学成立了应用力学系。克莱因主张并敦促哥廷根大学聘用了大批当时最优秀的自然科学家,例如 1895 年把希尔伯特从哥尼斯堡大学以正教授引进。1900 年,希尔伯特便以克莱因的“埃尔朗根纲领”为基础扛起了世界数学家首领的大旗。希尔伯特也十分关注物理学,还专门把他认为“数学较差”的爱因斯坦请到哥廷根大学讨论后来被称为爱因斯坦方程的物理学含义。讨论中,哥德尔为爱因斯坦方程找到了一个精确解,让他满载而归。1902 年,克莱因把闵可夫斯基请到哥廷根大学任教,他是几何学大师和数学物理学科创始人之一,是爱因斯坦的数学老师,他为爱因斯坦日后创立相对论奠定了坚实的数学理论支撑,去世时年仅 45 岁。1926 年春,希尔伯特又把冯·诺依曼(John von Neumann,1903-1957)请到哥廷根大学担任他的助手。1904 年,克莱因还把卡尔·龙格(Carl Runge,1856-1927)请到了哥廷根工作,同时推荐了工程学出身的路德维希·普朗特(Ludwig Prandtl,1875-1953)为应用力学系主任。以普朗特和他的学生冯·卡门(Theodore von Kármán,1881-1963)为代表的近代力学学派首先在哥廷根大学成长发展, 那是和克莱因的努力分不开的。冯·卡门于 1930 年移居美国,任职加州理工大学并培养出中国学生钱学森、钱伟长和郭永怀。普朗特在哥廷根留下的另一个著名力学家学生是赫尔曼·施里 希廷(Hermann Schlichting ,1907-1982)。其它例子包括 1905 年到访哥廷根大学的斯蒂芬·铁摩辛柯(Stephen Timoshenko,1878-1972)、1909 年到任的爱德蒙·朗道(Edmund Landau,1877-1938)以及 1920 年述职的理查德·柯朗。事实上,要列出克莱因时期一个连短期访客都包括在内的清单是累赘困难的,即使只限于数学方面人们也很容易就能列举诸如霍普 夫(Heinz Hopf)、阿廷(Emil Artin)、亚历山大洛夫(P. S. Alexandroff)、范德瓦尔登(Bartel van der Waerden)、费勒(William Feller)和波利亚(George Polya)。外尔曾经 写道:“克莱因像上帝般地统治着哥廷根,他神一样的力量主要来自于他的个性和对工作的热心奉献以及做好事情的能力。”
由于克莱因的卓越领导,哥廷根大学还不断开辟出新的交叉学科。仅在 1896 至 1907 年间,该校就诞生了世界上最早的物理化学、电化学、地球物理学、应用数学、应用力学、应用电子学, 并在这六个新学科都引进了首屈一指的领衔教授。在那些自然科学最为基础的学科如物理化学以及医学中,哥廷根大学也开辟了许多新的专业方向,推动并实现了哥廷根大学从人文社会科学向自然科学转移。事实上,哥廷根大学的科学家们在第一次世界大战前,在希尔伯特、德拜、 弗兰克、哈恩、玻恩等人的领导下,就已经开始了原子核物理方面的研究,从而使哥廷根成为最早的“世界原子核物理中心”。后来成为美国原子弹之父的奥本海默以及曼哈顿工程中最为杰出的一批科学家全都是当年哥廷根大学勤奋好学的年轻学子。有趣的是,多年之后,在 1955 年 4 月 12 日由 18 位联邦德国的原子物理学家和诺贝尔奖得主联名发表了著名的《哥廷根宣 言》,告诫各国政府使用氢弹的核战争将给人类带来毁灭性的灾难,敦促他们放弃以武力作为实现政治目的的手段,表达了科学家强烈的社会责任感。
哥廷根大学和哥廷根学派后来的低落完全归罪于纳粹。1930-40 年代第二次世界大战时期,希特勒迫害犹太人的黑色恐怖涂炭了哥廷根大学,迫使几乎所有的哥廷根学派成员移居美国。这个历史转折让哥廷根大学从此一蹶不振,却无意中帮助当时学术自由、包容并蓄的美国成就了 新的一代辉煌。
《哥廷根数学天空的闪烁群星》图片
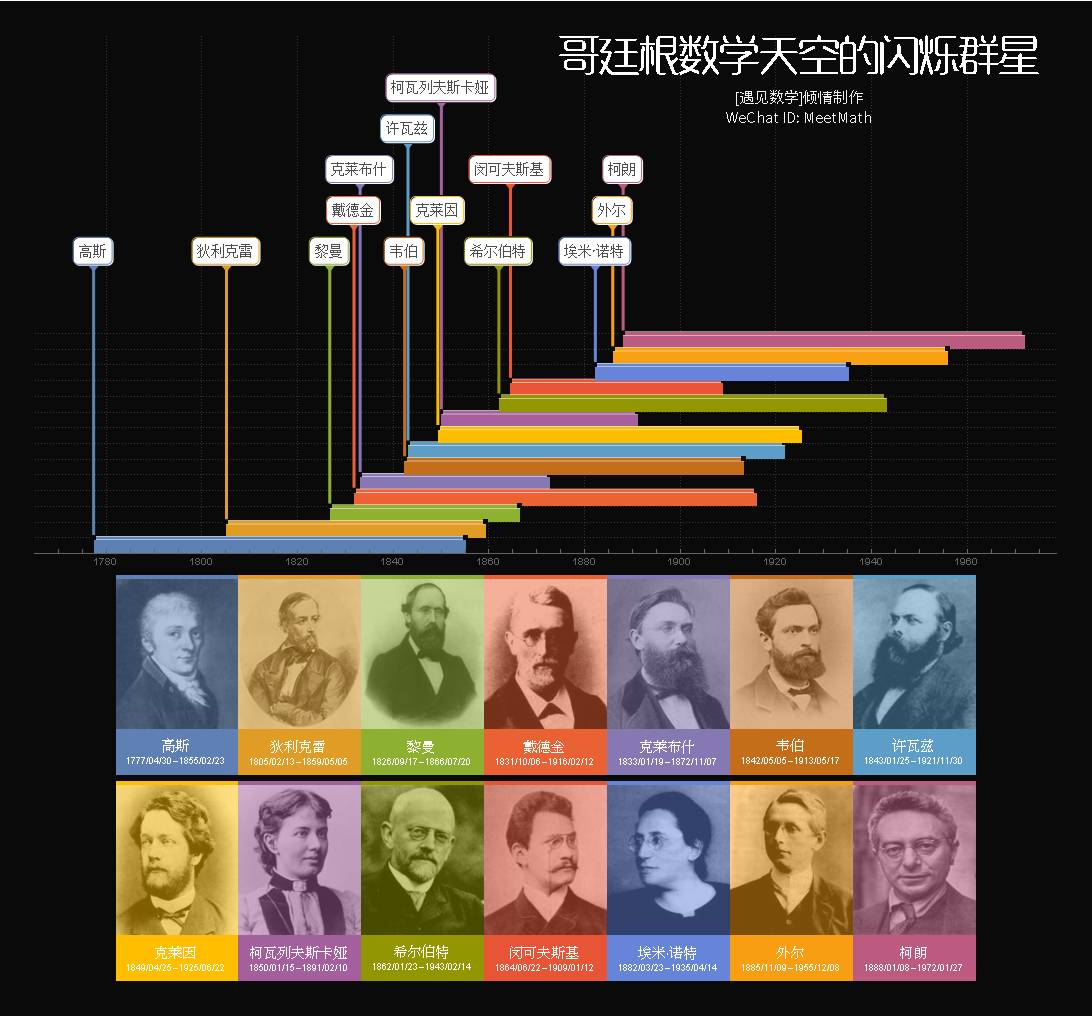
如想获取高清大图, 联系[遇见数学] - 公理(WeChat ID: meetmath_axiom) 获取.

公众号下次预告

8 月 10 日
《爱丽丝背后的故事》- 文化脉络中的数学 05
《爱丽丝梦游仙境》的创造者 - 路易斯·卡罗以及他的作品, 为什么说这个故事其实是写给成年人看的童话故事呢?

左图中的女孩就是传闻中爱丽丝的原型与灵感来源.
制作 | 公理
「予人玫瑰, 手留余香」
非常感谢您点击底部广告, 支持本号更快发展!
不用下载, 不用关注, 点开关掉即可





