Posits，一种新的数字表示方法，改进了人工智能的数学计算

2022 年 10 月 27 日 THU数据派

  
  
    
   
   
     
    
    
      
     
     
       
      
      
        
       
       
          
          来源：Science AI 
         
      
      
        
     
     
       
    
    
      
   
   
     
  
  
    
  
  
    
   
   
     
    
    
      
     
     
       
      
      
        
       
       
          
            本文为约1898字，建议阅读3分钟 
           
           本文 
           介绍了第一个基于位置的处理器内核。

训练许多现代 AI 工具背后的大型神经网络需要真正的计算能力：例如，OpenAI 最先进的语言模型 GPT-3 需要惊人的数亿次操作来训练，并且花费了大约 500 万美元的计算时间。工程师们认为他们已经找到了一种通过使用不同的数字表示方式来减轻负担的方法。

早在 2017 年，当时在 A*STAR 计算资源中心和新加坡国立大学联合任命的 John Gustafson 和当时在 Interplanetary Robot and Electric Brain Co. 任职的 Isaac Yonemoto 开发了一种表示数字的新方法。这些数字，称为 posits，被提议作为对当今使用的标准浮点算术处理器的改进。

现在，马德里康普顿斯大学的一组研究人员开发了第一个在硬件中实现 posit 标准的处理器内核，并表明，基本计算任务的精度逐位提高了四个数量级，与使用标准浮点数进行计算相比。他们在第29届 IEEE 计算机算术研讨会上展示了他们的结果。

论文链接：

https://spectrum.ieee.org/floating-point-numbers-posits-processor

「如今，摩尔定律似乎开始消退。」康普顿斯公司 ArTeCS 小组的研究生研究员 David Mallasén Quintana 说，「因此，我们需要找到一些其他方法来从同一台机器中获得更多性能。做到这一点的方法之一是改变我们对实数进行编码的方式，以及我们表示它们的方式。」

Complutense 团队并不是唯一一个用数字表示来挑战极限的人。近期，英伟达、Arm 和英特尔就使用 8 位浮点数而不是通常的 32 位或 16 位机器学习应用程序达成了一项规范。使用更小、更不精确的格式可以提高效率和内存使用率，但代价是计算准确性。

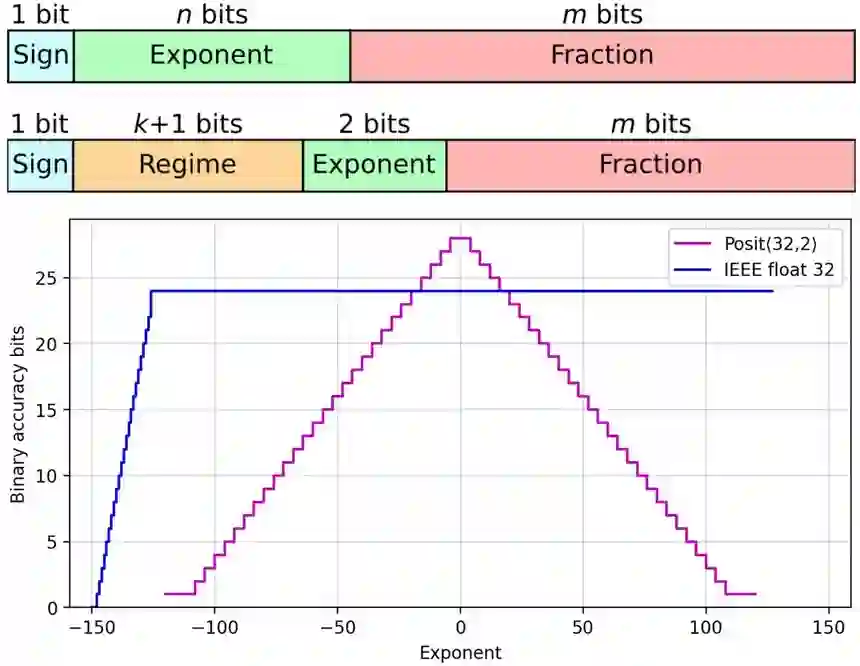
实数不能简单地用硬件完美地表示，因为它们的数量是无限的。为了适应指定的位数，许多实数必须四舍五入。Posits 的优势在于它们准确代表的数字沿数轴分布的方式。在数轴的中间，大约 1 和 -1，有比浮点更多的位置表示。在两翼，对于大的负数和正数，定位精度比浮点数下降得更优雅。

「它更适合计算中数字的自然分布。」Gustafson 说，「这是正确的动态范围，在您需要更高精度的情况下，它是正确的精度。浮点运算中有大量的位模式，从来没有人使用过。那是浪费！」

由于表示中的一个额外组件，Posits 在 1 和 -1 左右实现了这种改进的准确性。浮点数由三部分组成：一个符号位（0 表示正数，1 表示负数），几个「尾数」（分数）位表示小数点的二进制版本之后的内容，其余位定义指数（2^exp）。

Posits 保留了浮点数的所有组件，但添加了一个额外的「制度」部分，即指数的指数。该制度的美妙之处在于它的位长可以变化。对于小数字，它可能只需要两位，为尾数留下更高的精度。这允许在 1 和 -1 附近的最佳位置中进行更高的定位精度。

深度神经网络通常使用称为权重的归一化参数，使其成为受益于位置优势的完美候选者。大部分神经网络计算由乘法累加操作组成。每次执行这样的计算时，每个总和都必须重新截断，导致精度损失。使用 posits，称为 quire 的特殊寄存器可以有效地执行累加步骤以减少精度损失。但是今天的硬件实现了浮点数，到目前为止，在软件中使用 posits 的计算收益在很大程度上被格式之间转换的损失所掩盖。

借助在现场可编程门阵列（FPGA）中合成的新硬件实现，Complutense 团队能够并排比较使用 32 位浮点数和 32 位位置完成的计算。他们通过将它们与使用更准确但计算成本更高的 64 位浮点格式的结果进行比较来评估它们的准确性。Posits 在矩阵乘法（神经网络训练中固有的一系列乘法累加）的准确性方面显示出惊人的四个数量级的提高。他们还发现，提高精度并没有以计算时间为代价，只是稍微增加了芯片面积和功耗。

尽管数值精度的提高是不可否认的，但这究竟会如何影响像 GPT-3 这样的大型 AI 的训练还有待观察。

「假设可能会加快训练速度，因为你不会在途中丢失太多信息。」Mallasén 说，「但这些都是我们不知道的事情。有些人已经在软件中进行了尝试，但我们现在也想在硬件中进行尝试。」

其他团队正在开发他们自己的硬件实现以促进 posit 的使用。「它正在做我希望它会做的事情；它被疯狂地采用了。」Gustafson 说，「位置编号格式引起了轰动，有数十个团体，包括公司和大学，都在使用它。」