深度学习笔记系列(一):导数,梯度与方向导数
最近看论文的时候会感觉自己有很多基础的部分不是很扎实,所以准备系统地整理一下这些知识,并且记录下来。
这一部分的笔记之后会包括高等数学,线性代数,概率论,机器学习,信息论深度学习的相关知识以及其应用,之后也会慢慢的更新。
知乎传送门:https://zhuanlan.zhihu.com/p/93294877
第一篇讲的是导数,梯度和方向导数。
导数
单变量导数的一阶导数
对于单变量来说,其导数的计算方法如下:
导数代表的意义是函数在x处的变化率,当导数为0时x可能为函数的鞍点或者极值点。
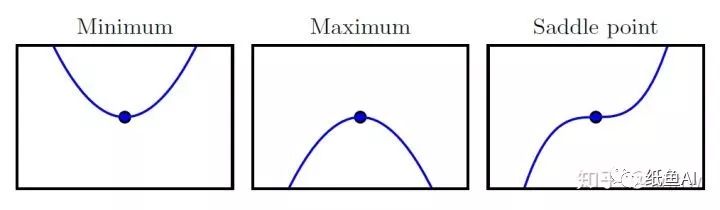
单变量函数的二阶导数
二阶导数代表的意义是函数在x点处导数的变化率。
二阶导数的计算方式如下:
二阶导数为0,说明该点的导数变化率为0。
偏导数
当一个函数有多个变量,而你只想计算函数与某个变量的变化关系时,就需要计算偏导数。
偏导数的计算方式如下:
当函数在某点 
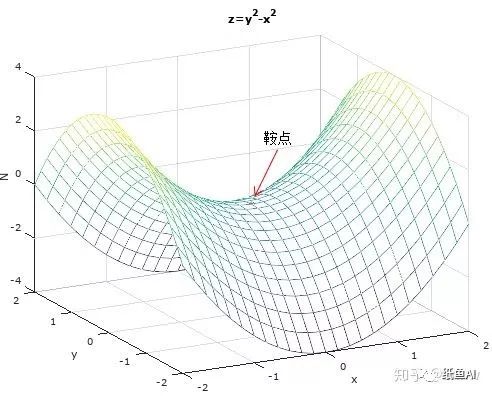
梯度
在机器学习的学习中,梯度这一词想必大家都不陌生,多元函数的所有偏导数构成的向量即为梯度。
梯度的本意是一个向量,表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大,为该梯度的模。
方向导数
从上面的内容大家可以看到偏导数只能描绘x,y方向上函数的变化率,但是在实际的使用过程中,我们想知道函数在各个方向上的变化率,于是就有了方向导数的概念。
方向导数是一个标量,方向导数定义了点 x 处沿向量 v 方向变化时,对应的函数的瞬时变化率。其中v为:
将v变为单位向量v'后,通过计算:
就可以得到函数在这个方向上的方向导数。
所有的文章整理后会发布在 https://github.com/linhaow/DLnotes
本文转载在公众号:纸鱼AI,作者:linhw
推荐阅读
Transformer详解《attention is all your need》论文笔记
关于AINLP
AINLP 是一个有趣有AI的自然语言处理社区,专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享,主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等,欢迎关注!加技术交流群请添加AINLP君微信(id:AINLP2),备注工作/研究方向+加群目的。











