机器学习(12)之决策树总结与python实践(~附源码链接~)

微信公众号

关键字全网搜索最新排名

【机器学习算法】：排名第一

【机器学习】：排名第二

【Python】：排名第三

【算法】：排名第四

前言

在（机器学习(9)之ID3算法详解及python实现）中讲到了ID3算法，在（机器学习(11)之C4.5详解与Python实现（从解决ID3不足的视角））中论述了ID3算法的改进版C4.5算法。对于C4.5算法，也提到了它的不足，比如模型是用较为复杂的熵来度量，使用了相对较为复杂的多叉树，只能处理分类不能处理回归等。对于这些问题， CART算法大部分做了改进。由于CART算法可以做回归，也可以做分类，本文以CART作为分类树来论述。

最优特征选择方法

在ID3算法中使用了信息增益来选择特征，信息增益大的优先选择。在C4.5算法中采用了信息增益比来选择特征，以减少信息增益容易选择特征值多的特征的问题。但是无论ID3还是C4.5,都是基于信息论的熵模型的，这里面会涉及大量的对数运算。能不能简化模型同时也不至于完全丢失熵模型的优点呢？有！CART分类树算法使用基尼系数来代替信息增益比，基尼系数代表了模型的不纯度，基尼系数越小，则不纯度越低，特征越好。这和信息增益(比)是相反的。

在分类问题中，假设有K个类别，第k个类别的概率为pk, 则基尼系数的表达式为：

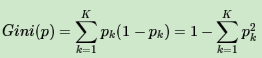
若是二类分类问题，计算就更简单了，如果属于第一个样本输出的概率是p，则基尼系数的表达式为：

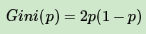
对于给定样本D,假设有K个类别, 第k个类别的数量为Ck,则样本D的基尼系数表达式为：

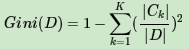
特别的，对于样本D,如果根据特征A的某个值a,把D分成D1和D2两部分，则在特征A的条件下，D的基尼系数表达式为：

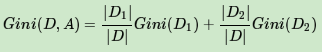
为了进一步简化，CART分类树算法每次仅仅对某个特征的值进行二分，而不是多分，这样CART分类树算法建立起来的是二叉树，而不是多叉树。这样一可以进一步简化基尼系数的计算，二可以建立一个更加优雅的二叉树模型。

连续特征的处理

对于CART分类树连续值的处理问题，其思想和C4.5是相同的，都是将连续的特征离散化。唯一的区别在于在选择划分点时的度量方式不同，C4.5使用的是信息增益，则CART分类树使用的是基尼系数。

具体的思路如下（与C4.5一致），比如m个样本的连续特征A有m个，从小到大排列为a1,a2,...,am,则CART算法取相邻两样本值的中位数，一共取得m-1个划分点，其中第i个划分点表示Ti表示为：Ti=ai+ai+12。对于这m-1个点，分别计算以该点作为二元分类点时的基尼系数。选择基尼系数最小的点作为该连续特征的二元离散分类点。

 

对于CART分类树离散值的处理问题，采用的思路是不停的二分离散特征。回忆下ID3或者C4.5，如果某个特征A被选取建立决策树节点，如果它有A1,A2,A3三种类别，我们会在决策树上一下建立一个三叉的节点。这样导致决策树是多叉树。但是CART分类树使用的方法不同，他采用的是不停的二分，还是这个例子，CART分类树会考虑把A分成和{A1}和{A2,A3}, 和{A2}和{A1,A3}, 和{A3}和{A1,A2}三种情况，找到基尼系数最小的组合，比如和{A2}和{A1,A3},然后建立二叉树节点，一个节点是A2对应的样本，另一个节点是{A1,A3}对应的节点。同时，由于这次没有把特征A的取值完全分开，后面我们还有机会在子节点继续选择到特征A来划分A1和A3。这和ID3或者C4.5不同，在ID3或者C4.5的一棵子树中，离散特征只会参与一次节点的建立。

CART建树流程

算法输入是训练集D，基尼系数的阈值，样本个数阈值。

算法输出是决策树T。

　1) 对于当前节点的数据集为D，如果样本个数小于阈值或者没有特征，则返回决策子树，当前节点停止递归。

　2) 计算样本集D的基尼系数，如果基尼系数小于阈值，则返回决策树子树，当前节点停止递归。

　3) 计算当前节点现有的各个特征的各个特征值对数据集D的基尼系数，对于离散值和连续值的处理方法和基尼系数的计算见上一节。

　4) 在计算出来的各个特征的各个特征值对数据集D的基尼系数中，选择基尼系数最小的特征A和对应的特征值a。根据这个最优特征和最优特征值，把数据集划分成两部分D1和D2，同时建立当前节点的左右节点，做节点的数据集D为D1，右节点的数据集D为D2.

　5) 对左右的子节点递归的调用1-4步，生成决策树。

剪枝

由于决策时算法很容易对训练集过拟合，而导致泛化能力差，为了解决这个问题，我们需要对CART树进行剪枝，即类似于线性回归的正则化，来增加决策树的返回能力。但是，有很多的剪枝方法，我们应该这么选择呢？CART采用的办法是后剪枝法，即先生成决策树，然后产生所有可能的剪枝后的CART树，然后使用交叉验证来检验各种剪枝的效果，选择泛化能力最好的剪枝策略。

第一步是从原始决策树生成各种剪枝效果的决策树；

第二步是用交叉验证来检验剪枝后的预测能力，选择泛化预测能力最好的剪枝后的数作为最终的CART树。

在剪枝的过程中，对于任意的一刻子树T,其损失函数为：

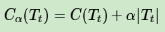
其中，α为正则化参数，C(Tt)为训练数据的预测误差，分类树是用基尼系数度量，回归树是均方差度量。|Tt|是子树T的叶子节点的数量。

当α=0时，即没有正则化，原始的生成的CART树即为最优子树。当α=∞时，即正则化强度达到最大，此时由原始的生成的CART树的根节点组成的单节点树为最优子树。一般来说，α越大，则剪枝剪的越厉害，生成的最优子树相比原生决策树就越偏小。对于固定的α，一定存在使损失函数Cα(T)最小的唯一子树。

对于位于节点t的任意一颗子树Tt，如果没有剪枝，它的损失是上面的那个公式。如果将其剪掉，仅仅保留根节点，则损失是

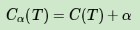
如果满足下式：

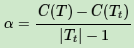
Tt和T有相同的损失函数，但是T节点更少，因此可以对子树Tt进行剪枝，也就是将它的子节点全部剪掉，变为一个叶子节点T。

剪枝流程

输入是CART树建立算法得到的原始决策树T。

输出是最优决策子树Tα。

算法过程如下：

　1）初始化αmin=∞， 最优子树集合ω={T}。

　2）从叶子节点开始自下而上计算各内部节点t的训练误差损失函数Cα(Tt)（回归树为均方差，分类树为基尼系数）, 叶子节点数|Tt|，以及正则化阈值α=min{C(T)−C(Tt)|Tt|−1,αmin}, 更新αmin=α

　3) 得到所有节点的α值的集合M。

　4）从M中选择最大的值αk，自上而下的访问子树t的内部节点，如果(C(T)−C(Tt))/(|Tt|−1)≤αk时，进行剪枝。并决定叶节点t的值。如果是分类树，则是概率最高的类别，如果是回归树，则是所有样本输出的均值。这样得到αk对应的最优子树Tk

　5）最优子树集合ω=ω∪Tk， M=M−{αk}。

　6) 如果M不为空，则回到步骤4。否则就已经得到了所有的可选最优子树集合ω.

　7) 采用交叉验证在ω选择最优子树

三类算法对比

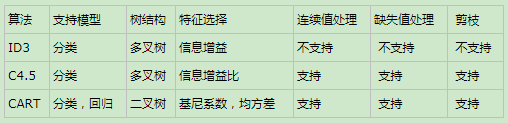
优点

1）简单直观，生成的决策树很直观。

2）基本不需要预处理，不需要提前归一化，处理缺失值。

3）使用决策树预测的代价是O(log2m)。 m为样本数。

4）既可以处理离散值也可以处理连续值。很多算法只是专注于离散值或者连续值。

5）可以处理多维度输出的分类问题。

6）相比于神经网络之类的黑盒分类模型，决策树在逻辑上可以得到很好的解释

7）可以交叉验证的剪枝来选择模型，从而提高泛化能力。

8） 对于异常点的容错能力好，健壮性高。

缺点

1）决策树算法非常容易过拟合，导致泛化能力不强。可以通过设置节点最少样本数量和限制决策树深度来改进。

2）决策树会因为样本发生一点点的改动，就会导致树结构的剧烈改变。这个可以通过集成学习之类的方法解决。

3）寻找最优的决策树是一个NP难的问题，我们一般是通过启发式方法，容易陷入局部最优。可以通过集成学习之类的方法来改善。

4）有些比较复杂的关系，决策树很难学习，比如异或。这个就没有办法了，一般这种关系可以换神经网络分类方法来解决。

5）如果某些特征的样本比例过大，生成决策树容易偏向于这些特征。这个可以通过调节样本权重来改善。

CART实战

数据参照 《机器学习-周志华》 一书中的决策树一章。

代码则参照《机器学习实战》一书的内容，并做了一些修改。

源码下载方式

1. 添加微信交流群

   （加我微信：guodongwe1991,备注姓名-单位-研究方向）

2. 后台回复关键词：170821

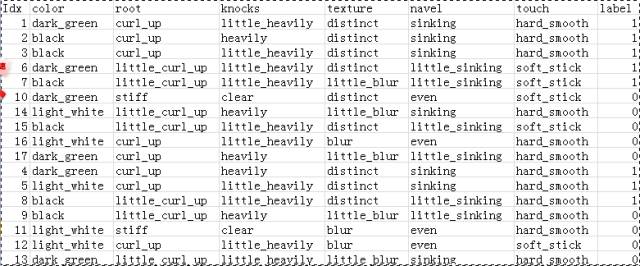
其中，前11个数据用作训练集（1, 2, 3, 6, 7, 10, 14, 15, 16, 17, 4），后6个数据用作测试集（5,8,9,11,12,13）

CART.py（代码233行）

# -*- coding: utf-8 -*-

from numpy import *

import numpy as np

import pandas as pd

from math import log

import operator

#计算数据集的基尼指数

def calcGini(dataSet):

    numEntries=len(dataSet)

    labelCounts={}

    #给所有可能分类创建字典

    for featVec in dataSet:

        currentLabel=featVec[-1]

        if currentLabel not in labelCounts.keys():

            labelCounts[currentLabel]=0

        labelCounts[currentLabel]+=1

    Gini=1.0

    #以2为底数计算香农熵

    for key in labelCounts:

        prob = float(labelCounts[key])/numEntries

        Gini-=prob*prob

    return Gini

#对离散变量划分数据集，取出该特征取值为value的所有样本

def splitDataSet(dataSet,axis,value):

    retDataSet=[]

    for featVec in dataSet:

        if featVec[axis]==value:

            reducedFeatVec=featVec[:axis]

            reducedFeatVec.extend(featVec[axis+1:])

            retDataSet.append(reducedFeatVec)

    return retDataSet

#对连续变量划分数据集，direction规定划分的方向，

#决定是划分出小于value的数据样本还是大于value的数据样本集

def splitContinuousDataSet(dataSet,axis,value,direction):

    retDataSet=[]

    for featVec in dataSet:

        if direction==0:

            if featVec[axis]>value:

                reducedFeatVec=featVec[:axis]

                reducedFeatVec.extend(featVec[axis+1:])

                retDataSet.append(reducedFeatVec)

        else:

            if featVec[axis]<=value:

                reducedFeatVec=featVec[:axis]

                reducedFeatVec.extend(featVec[axis+1:])

                retDataSet.append(reducedFeatVec)

    return retDataSet

#选择最好的数据集划分方式

def chooseBestFeatureToSplit(dataSet,labels):

    numFeatures=len(dataSet[0])-1

    bestGiniIndex=100000.0

    bestFeature=-1

    bestSplitDict={}

    for i in range(numFeatures):

        featList=[example[i] for example in dataSet]

        #对连续型特征进行处理

        if type(featList[0]).__name__=='float' or type(featList[0]).__name__=='int':

            #产生n-1个候选划分点

            sortfeatList=sorted(featList)

            splitList=[]

            for j in range(len(sortfeatList)-1):

                splitList.append((sortfeatList[j]+sortfeatList[j+1])/2.0)

            

            bestSplitGini=10000

            slen=len(splitList)

            #求用第j个候选划分点划分时，得到的信息熵，并记录最佳划分点

            for j in range(slen):

                value=splitList[j]

                newGiniIndex=0.0

                subDataSet0=splitContinuousDataSet(dataSet,i,value,0)

                subDataSet1=splitContinuousDataSet(dataSet,i,value,1)

                prob0=len(subDataSet0)/float(len(dataSet))

                newGiniIndex+=prob0*calcGini(subDataSet0)

                prob1=len(subDataSet1)/float(len(dataSet))

                newGiniIndex+=prob1*calcGini(subDataSet1)

                if newGiniIndex<bestSplitGini:

                    bestSplitGini=newGiniIndex

                    bestSplit=j

            #用字典记录当前特征的最佳划分点

            bestSplitDict[labels[i]]=splitList[bestSplit]

            

            GiniIndex=bestSplitGini

        #对离散型特征进行处理

        else:

            uniqueVals=set(featList)

            newGiniIndex=0.0

            #计算该特征下每种划分的信息熵

            for value in uniqueVals:

                subDataSet=splitDataSet(dataSet,i,value)

                prob=len(subDataSet)/float(len(dataSet))

                newGiniIndex+=prob*calcGini(subDataSet)

            GiniIndex=newGiniIndex

        if GiniIndex<bestGiniIndex:

            bestGiniIndex=GiniIndex

            bestFeature=i

    #若当前节点的最佳划分特征为连续特征，则将其以之前记录的划分点为界进行二值化处理

    #即是否小于等于bestSplitValue

    if type(dataSet[0][bestFeature]).__name__=='float' or type(dataSet[0][bestFeature]).__name__=='int':      

        bestSplitValue=bestSplitDict[labels[bestFeature]]        

        labels[bestFeature]=labels[bestFeature]+'<='+str(bestSplitValue)

        for i in range(shape(dataSet)[0]):

            if dataSet[i][bestFeature]<=bestSplitValue:

                dataSet[i][bestFeature]=1

            else:

                dataSet[i][bestFeature]=0

    return bestFeature

#特征若已经划分完，节点下的样本还没有统一取值，则需要进行投票

def majorityCnt(classList):

    classCount={}

    for vote in classList:

        if vote not in classCount.keys():

            classCount[vote]=0

        classCount[vote]+=1

    return max(classCount)

#主程序，递归产生决策树

def createTree(dataSet,labels,data_full,labels_full):

    classList=[example[-1] for example in dataSet]

    if classList.count(classList[0])==len(classList):

        return classList[0]

    if len(dataSet[0])==1:

        return majorityCnt(classList)

    bestFeat=chooseBestFeatureToSplit(dataSet,labels)

    bestFeatLabel=labels[bestFeat]

    myTree={bestFeatLabel:{}}

    featValues=[example[bestFeat] for example in dataSet]

    uniqueVals=set(featValues)

    if type(dataSet[0][bestFeat]).__name__=='str':

        currentlabel=labels_full.index(labels[bestFeat])

        featValuesFull=[example[currentlabel] for example in data_full]

        uniqueValsFull=set(featValuesFull)

    del(labels[bestFeat])

    #针对bestFeat的每个取值，划分出一个子树。

    for value in uniqueVals:

        subLabels=labels[:]

        if type(dataSet[0][bestFeat]).__name__=='str':

            uniqueValsFull.remove(value)

        myTree[bestFeatLabel][value]=createTree(splitDataSet\

         (dataSet,bestFeat,value),subLabels,data_full,labels_full)

    if type(dataSet[0][bestFeat]).__name__=='str':

        for value in uniqueValsFull:

            myTree[bestFeatLabel][value]=majorityCnt(classList)

    return myTree

#由于在Tree中，连续值特征的名称以及改为了  feature<=value的形式

#因此对于这类特征，需要利用正则表达式进行分割，获得特征名以及分割阈值

def classify(inputTree,featLabels,testVec):

    firstStr=inputTree.keys()[0]

    if '<=' in firstStr:

        featvalue=float(re.compile("(<=.+)").search(firstStr).group()[2:])

        featkey=re.compile("(.+<=)").search(firstStr).group()[:-2]

        secondDict=inputTree[firstStr]

        featIndex=featLabels.index(featkey)

        if testVec[featIndex]<=featvalue:

            judge=1

        else:

            judge=0

        for key in secondDict.keys():

            if judge==int(key):

                if type(secondDict[key]).__name__=='dict':

                    classLabel=classify(secondDict[key],featLabels,testVec)

                else:

                    classLabel=secondDict[key]

    else:

        secondDict=inputTree[firstStr]

        featIndex=featLabels.index(firstStr)

        for key in secondDict.keys():

            if testVec[featIndex]==key:

                if type(secondDict[key]).__name__=='dict':

                    classLabel=classify(secondDict[key],featLabels,testVec)

                else:

                    classLabel=secondDict[key]

    return classLabel

#测试决策树正确率

def testing(myTree,data_test,labels):

    error=0.0

    for i in range(len(data_test)):

        if classify(myTree,labels,data_test[i])!=data_test[i][-1]:

            error+=1

    #print 'myTree %d' %error

    return float(error)

#测试投票节点正确率

def testingMajor(major,data_test):

    error=0.0

    for i in range(len(data_test)):

        if major!=data_test[i][-1]:

            error+=1

    #print 'major %d' %error

    return float(error)

#后剪枝

def postPruningTree(inputTree,dataSet,data_test,labels):

    firstStr=inputTree.keys()[0]

    secondDict=inputTree[firstStr]

    classList=[example[-1] for example in dataSet]

    featkey=copy.deepcopy(firstStr)

    if '<=' in firstStr:

        featkey=re.compile("(.+<=)").search(firstStr).group()[:-2]

        featvalue=float(re.compile("(<=.+)").search(firstStr).group()[2:])

    labelIndex=labels.index(featkey)

    temp_labels=copy.deepcopy(labels)

    del(labels[labelIndex])

    for key in secondDict.keys():

        if type(secondDict[key]).__name__=='dict':

            if type(dataSet[0][labelIndex]).__name__=='str':

                inputTree[firstStr][key]=postPruningTree(secondDict[key],\

                 splitDataSet(dataSet,labelIndex,key),splitDataSet(data_test,labelIndex,key),copy.deepcopy(labels))

            else:

                inputTree[firstStr][key]=postPruningTree(secondDict[key],\

                splitContinuousDataSet(dataSet,labelIndex,featvalue,key),\

                splitContinuousDataSet(data_test,labelIndex,featvalue,key),\

                copy.deepcopy(labels))

    if testing(inputTree,data_test,temp_labels)<=testingMajor(majorityCnt(classList),data_test):

        return inputTree

    return majorityCnt(classList)

df=pd.read_csv('data.csv')

data=df.values[:11,1:].tolist()

data_full=data[:]

labels=df.columns.values[1:-1].tolist()

labels_full=labels[:]

myTree=createTree(data,labels,data_full,labels_full)

data=df.values[:11,1:].tolist()

data_test=df.values[11:,1:].tolist()

labels=df.columns.values[1:-1].tolist()

myTree=postPruningTree(myTree,data,data_test,labels)

import plotTree

plotTree.createPlot(myTree)

plotTree.py（代码72行）

import matplotlib.pyplot as plt  

decisionNode=dict(boxstyle="sawtooth",fc="0.8")  

leafNode=dict(boxstyle="round4",fc="0.8")  

arrow_args=dict(arrowstyle="<-")  

  

#计算树的叶子节点数量  

def getNumLeafs(myTree):  

    numLeafs=0  

    firstStr=myTree.keys()[0]  

    secondDict=myTree[firstStr]  

    for key in secondDict.keys():  

        if type(secondDict[key]).__name__=='dict':  

            numLeafs+=getNumLeafs(secondDict[key])  

        else: numLeafs+=1  

    return numLeafs  

  

#计算树的最大深度  

def getTreeDepth(myTree):  

    maxDepth=0  

    firstStr=myTree.keys()[0]  

    secondDict=myTree[firstStr]  

    for key in secondDict.keys():  

        if type(secondDict[key]).__name__=='dict':  

            thisDepth=1+getTreeDepth(secondDict[key])  

        else: thisDepth=1  

        if thisDepth>maxDepth:  

            maxDepth=thisDepth  

    return maxDepth  

  

#画节点  

def plotNode(nodeTxt,centerPt,parentPt,nodeType):  

    createPlot.ax1.annotate(nodeTxt,xy=parentPt,xycoords='axes fraction',\  

    xytext=centerPt,textcoords='axes fraction',va="center", ha="center",\  

    bbox=nodeType,arrowprops=arrow_args)  

  

#画箭头上的文字  

def plotMidText(cntrPt,parentPt,txtString):  

    lens=len(txtString)  

    xMid=(parentPt[0]+cntrPt[0])/2.0-lens*0.002  

    yMid=(parentPt[1]+cntrPt[1])/2.0  

    createPlot.ax1.text(xMid,yMid,txtString)  

      

def plotTree(myTree,parentPt,nodeTxt):  

    numLeafs=getNumLeafs(myTree)  

    depth=getTreeDepth(myTree)  

    firstStr=myTree.keys()[0]  

    cntrPt=(plotTree.x0ff+(1.0+float(numLeafs))/2.0/plotTree.totalW,plotTree.y0ff)  

    plotMidText(cntrPt,parentPt,nodeTxt)  

    plotNode(firstStr,cntrPt,parentPt,decisionNode)  

    secondDict=myTree[firstStr]  

    plotTree.y0ff=plotTree.y0ff-1.0/plotTree.totalD  

    for key in secondDict.keys():  

        if type(secondDict[key]).__name__=='dict':  

            plotTree(secondDict[key],cntrPt,str(key))  

        else:  

            plotTree.x0ff=plotTree.x0ff+1.0/plotTree.totalW  

            plotNode(secondDict[key],(plotTree.x0ff,plotTree.y0ff),cntrPt,leafNode)  

            plotMidText((plotTree.x0ff,plotTree.y0ff),cntrPt,str(key))  

    plotTree.y0ff=plotTree.y0ff+1.0/plotTree.totalD  

  

def createPlot(inTree):  

    fig=plt.figure(1,facecolor='white')  

    fig.clf()  

    axprops=dict(xticks=[],yticks=[])  

    createPlot.ax1=plt.subplot(111,frameon=False,**axprops)  

    plotTree.totalW=float(getNumLeafs(inTree))  

    plotTree.totalD=float(getTreeDepth(inTree))  

    plotTree.x0ff=-0.5/plotTree.totalW  

    plotTree.y0ff=1.0  

    plotTree(inTree,(0.5,1.0),'')  

    plt.show()  

参考：

1. 周志华《机器学习》

2. 博客园：作者（刘建平）http://www.cnblogs.com/pinard/p/6053344.html

3. 李航 《统计学习方法》

4. http://www.codexiu.cn/python/blog/7899/

5. http://blog.csdn.net/wzmsltw/article/details/51039928

加我微信：guodongwe1991,备注姓名-单位-研究方向（加入微信机器学习交流1群）

招募 志愿者

广告、商业合作

请加QQ：357062955@qq.com

喜欢，别忘关注~

帮助你在AI领域更好的发展，期待与你相遇！