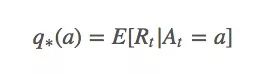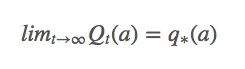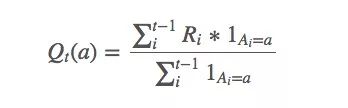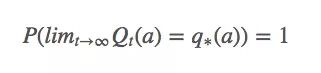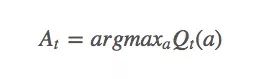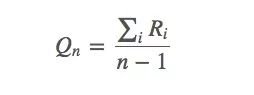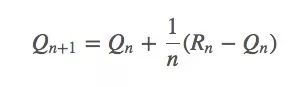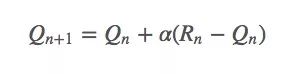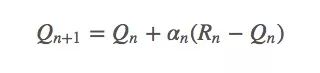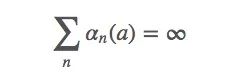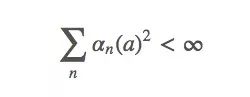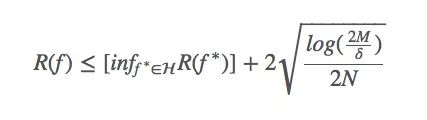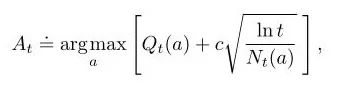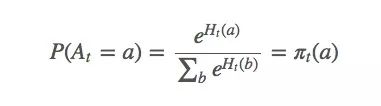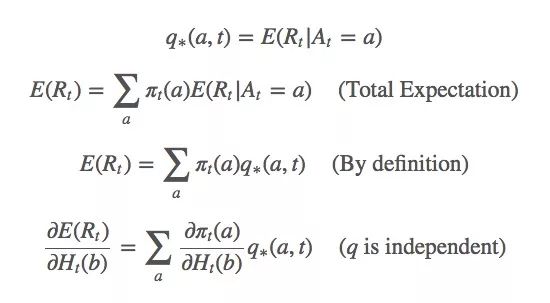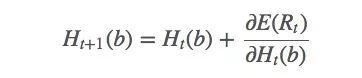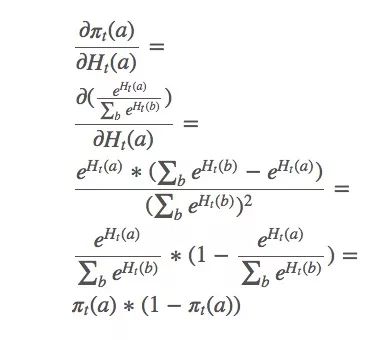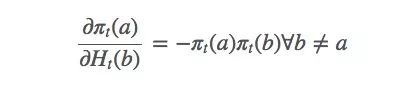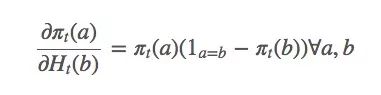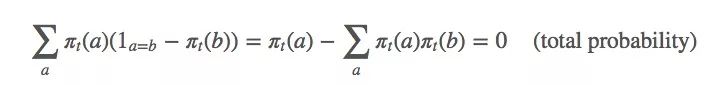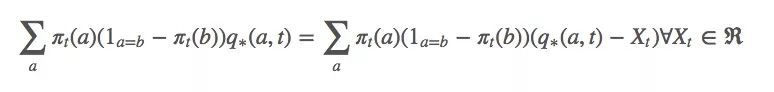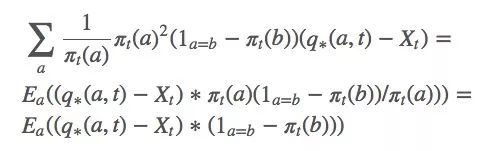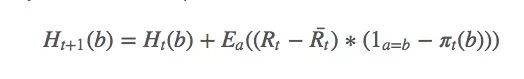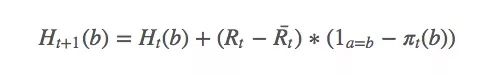强化学习——多臂老虎机问题
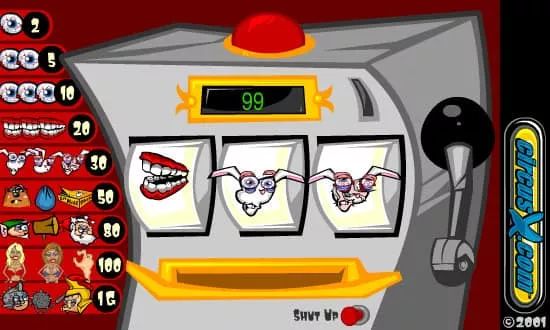
编者按:无论有没有去过赌场,相信大多数人都不会对老虎机感到陌生。作为赌场里最常见的娱乐设备,老虎机不仅在现实中广受人们欢迎,它也频繁出现在电视电影乃至动画片中,连一些常见的APP里都有它的身影。
往机器里投入硬币后,玩家需要拉下拉把转动玻璃框中的图案,如果三个图案一致,玩家能获得所有累积奖金;如果不一致,投入的硬币就会被吞入累积奖金池。这个问题看似简单,但很多人也许都忽视了,其实它和围棋、游戏一样,也是个强化学习问题。
首先,我们要明确一点——老虎机问题是表格型解决方案工具的一种。之所以这么说,是因为我们可以把所有可能的状态放进一个表格中,然后让表格告诉我们需要了解的问题状态,继而为解决问题找出切实的解决方案。
k-armed Bandit Problem
单臂老虎机:只有一根侧面拉杆
假设我们有一台K臂老虎机,每根拉杆都能提供固定的一定数额的金钱,一次只能拉下一根拉杆,但我们不知道它们的具体回报是多少。在这个情景中,k根拉杆可以被视为k种不同的动作(action),拉下拉杆的总次数T是我们的总timestep。整个任务的目标是实现收益的最大化。
设在第t次拉下拉杆时,我们采取的动作是At,当时获得的回报是Rt。那么对于任意动作a,它的动作值(value)q∗(a)是:
这个等式表示的是无论何时,如果我们选择动作a,我们获得的实际回报就应该等于动作a的预期回报。
把上面这个句子再读三四遍,你觉得它行得通吗?如果我们事先已经知道拉下这个拉杆的最大收益是多少,那出于贪婪的目的,我们肯定每次都会选最好的动作,然后使最终回报最大化。但在强化学习问题中,贪婪算法并不一定等同于最优策略,这一步的贪婪可能会对下一步产生负面影响。
虽然很困难,但我们真的很想实现q∗(a),所以对于timestep t,设Qt(a)是q∗(a)的近似值:
那么我们又该怎么获得Qt(a)?
注:上文中的回报(reward)和动作值(value)不是同一个概念。回报指的是执行动作后的当场回报,动作值是一个长期的回报。如果你吸毒了,一小时内你很high,回报很高,但长期来看,你获得的动作值就很可怕了。需要注意的是,因为赌博机只需要一个动作,所以这里的q∗(a)不是未来回报之和,只是期望回报,它和其他地方的q∗(a)也不一样(虽然有滥用符号之嫌,但还是请多包涵啦)。
动作值方法
函数Qπ(x, a)表示从状态x出发,执行动作a后再使用策略π带来的累计奖赏,称为“状态-动作值函数”(state-action value function)。——周志华《机器学习》
首先,我们需要估计动作值,再据此决定要采取的行动。
估算动作值
求解q∗(a)近似值的一种简单方法是使用样本平均值:
上述等式看起来好像有什么说法,但它其实很简单——选择动作a时,我们获得的平均回报是多少。这个均值可以被视为q∗(a)的近似值,因为换几个符号,我们就能发现这就是强大数定律(SLLN)的表达式。
换句话说,它意味着Qt(a)必须收敛于q∗(a):
比起概率收敛,这种收敛更强大,但它其实也没法保证Qt(a)一定能收敛。
动作选择规则:贪婪
“贪婪者总是一贫如洗。”当面对巨大诱惑时,一些人会因为贪婪越过自己的底线,去吸毒,去犯罪,但他们在获得短暂快感的同时也失去了更多东西。强化学习中同样存在类似的问题,如果它是贪婪的,它会找出迄今为止最大的动作值:
并依据这个动作值去选择每一步动作。这样做的后果是智能体从头到尾只会选择同一套动作,而从不去尝试其他动作,在很多情况下,这样的策略并不是最优策略。
动作选择规则:ϵ-Greedy
那么我们该怎么纠正它的贪婪?之前我们在《强化学习——蒙特卡洛方法介绍》一文中已经介绍过ε-greedy:对于任何时刻t的执行“探索”小概率ε<1,我们会有ε的概率会进行exploration,有1-ε的概率会进行exploitation。这可以简单理解成抛硬币,除了正面和反面,它还有一个极小的立起来的概率。
虽然当智能体“头脑发热”时,它还是会义无反顾地贪婪,但相比贪婪策略,ϵ-Greedy随机选择策略(不贪婪)的概率是ε/|A(s)|。
症结:非平稳的动作值
导致这种现象的主要原因是动作值会随时间推移发生变化,即之前我们研究的时静态地拉杆,而不是随机的、动态的拉杆。以动作值为例,比起我们之前假设的q∗(a),它更应该被表示成q∗(a, t)。
依据之前的动作值估计,我们有:
它也可以被写成:
看起来SGD可以在这里发挥一些作用。如果它是平稳的,那q∗(a)收敛的概率就是100%;如果它不平稳,我们一般不会希望Rn=Rn-1,因为当前回报会影响当前的动作值。
这里我们把权重1/n替换成α(α∈(0,1]):
这是一个指数平均值,它在几何上衰减之前回报的权重。设函数αn(a)是第n个timestep,也就是第n次拉下拉杆时某个特定奖励的权重。因为老虎机问题只需考虑动作a,所以这个函数也可以简化成α(a)。
为了保证上式能收敛,我们还需要一些其他条件。
条件一
上式表示对于任何初始值Q1∈ℜ,它都满足q∗(a)∈ℜ。这个条件要求保证timestep足够大,以最终克服任何初始条件或随机波动
条件二
这个式子表示这些timestep将“足够小以确保能收敛到一个小值”。简而言之,第二个条件保证最终timestep会变小,以保证收敛。
既然如此,我们之前为什么要设αn(a)=α∈(0,1]呢?它不是一个常数吗?这样的阈值会不会影响收敛?
这些猜想都是正确的,但(0,1]这个阈值也有它存在的价值。我们在之前的Qn+1=Qn+αn(Rn+Qn)上继续计算,最后可以获得一项α(1-α)n-iRi,因为α小于1,所以给予R的权重随着介入奖励次数的增加而减少。
因为最佳动作值时非平稳的,所以我们不想收敛到一个特定的价值。
动作选择规则:乐观的初始值
到目前为止,我们必须非常随意地设定Q1(a)的初始值,它本质上是一组用于初始化的超参数。这里有个小诀窍,我们可以设初始值Q1(a)=C∀a,其中C>q∗(a)∀a。
这样之后,因为Qn(a)比估计值偏高,这时智能体会积极探索其他动作,当它越来越接近q∗(a)时,智能体就开始贪婪了。换句话说,假设我们设当前拉杆的乐观回报是3,但智能体尝试一次后,发现回报只有1,低于预期值,于是它会把其他拉杆全部尝试一遍。虽然前期效率很低,但到后期,智能体已经掌握哪些拉杆会产生高值,效果就接近“贪婪”了。
这种方法时可行的,在某种程度上,如果时间充裕,这个过程也可以被看作是模拟退火。但从整体来看,乐观初始值前期的大量“exploration”是不必要的,它对于非平稳问题来说不是最好的答案。
动作选择规则:置信上限选择
在机器学习系统中,Bias与Variance往往不可兼得:如果要降低模型的Bias,就一定程度上会提高模型的Variance;如果要降低Variance,Bias就会不可避免地提高。针对两者间的trade-off,下面的式子是一个很好的总结:
其中,
R(f)是假设f的(理论上)的风险;
R(f< *)是在假设集H中,假设f的最小风险;
M是假设集|H|的大小;
N是其中的样本数;
δ是一个常数(如果非要知道这个常数是什么,只能说它是我们选择一个差的假设的概率)。
这里有两个重点:
样本数量非常少,我们的边界非常松散。我们不知道目前的假设是否是最好的假设。
我们的假设越大,PAC(近似正确)学习的约束就越松散。
置信上限(UCB)是一个非常强大的算法,它可以用类似Bias-Variance权衡的方法来解决不同的问题。在老虎机问题中,我们可以把timestep t当成假设集大小M,因为随着t逐渐增加,an也会逐渐增加,相应的At就很难选择。
每选一次a,不确定项就会减少,分母Nt(a)增加;另一方面,每一次选择了a以外的行为,t会增加但Nt(a)不会改变,不确定评估值会增加。
梯度老虎机算法
截至目前,我们一直在努力估计q∗(a),但如果说这个问题还有除了行动值以外的解决方法呢?比如我们该如何学习一个动作的偏好?
设动作偏好为Ht(a),它和回报无关,只是一个动作相对于另一个动作的重要性。那么At应该符合gibbs分布(也就是机器学习的softmax分布):
对于这个式子,我们该怎么基于梯度计算最大似然估计?首先,我们对Ht(a)做梯度上升,因为它是我们的变量。我们想最大化E(Rt):
Ht(a)的更新规则如下所示:
gibbs分布分解:
这只是整个梯度的一个偏导数。那么b≠a的动作呢?下面是省略计算过程的结果:
由此可得:
因为:
相应的,这个等式也是成立的:
由上述等式可得:
因为q∗(a,t)被包含在动作a的预期值内,它也可以被写成Rt。那等式里的Xt是什么?坦率地说,你想它是什么它就是什么,严谨起见,我们可以设Xt是Rt的平均值。
计算梯度后获得新的更新规则:
其中a是t时采取的动作。由于找到a的期望值很困难,我们可以用随机值来更新:
选择动作的简单方法是计算argmaxaπt(a),问题就解决了。
备注
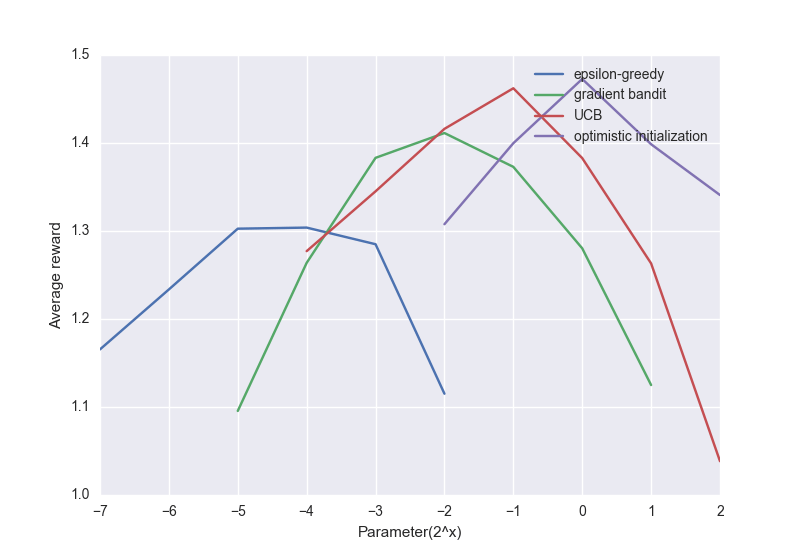
下面是上述算法的一个比较图:
尽管简单的方法表现不太好,但对很多强化学习问题来说,它们也称得上是最先进的算法了。
原文地址:oneraynyday.github.io/ml/2018/05/03/Reinforcement-Learning-Bandit/