Tensorflow 中 learning rate decay 的奇技淫巧
本文作者Elevanth,本文首发于知乎专栏【计算机视觉小白的调参之路】,AI 研习社获其授权转载。
深度学习中参数更新的方法想必大家都十分清楚了——sgd,adam 等等,孰优孰劣相关的讨论也十分广泛。可是,learning rate 的衰减策略大家有特别关注过吗?
说实话,以前我也只使用过指数型和阶梯型的下降法,并不认为它对深度学习调参有多大帮助。但是,最近的学习和工作中逐渐接触到了各种奇形怪状的 lr 策略,可以说大大刷新了三观,在此也和大家分享一下学习经验。
learning rate 衰减策略文件在 tensorflow/tensorflow/python/training/learning_rate_decay.py(http://t.cn/RQJ78Lg ) 中,函数中调用方法类似 tf.train.exponential_decay 就可以了。
以下,我将在 ipython 中逐个介绍各种 lr 衰减策略。
exponential_decay
exponential_decay(learning_rate, global_step, decay_steps, decay_rate,
staircase=False, name=None)
指数型 lr 衰减法是最常用的衰减方法,在大量模型中都广泛使用。
learning_rate 传入初始 lr 值,global_step 用于逐步计算衰减指数,decay_steps 用于决定衰减周期,decay_rate 是每次衰减的倍率,staircase 若为 False 则是标准的指数型衰减,True 时则是阶梯式的衰减方法,目的是为了在一段时间内(往往是相同的 epoch 内)保持相同的 learning rate。
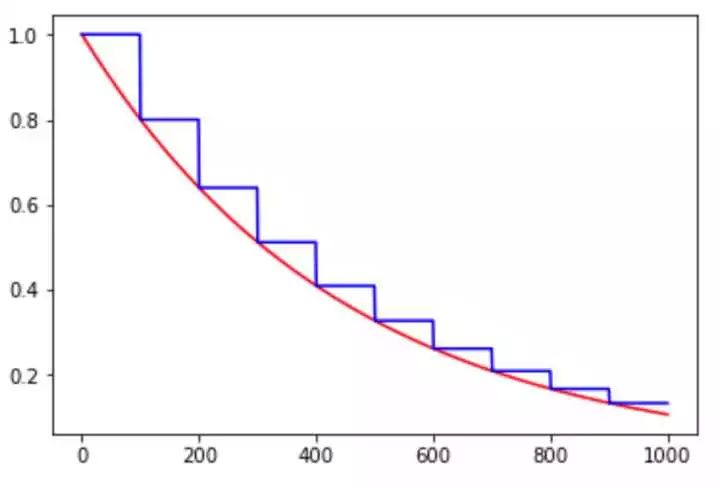
图 1. exponential_decay 示例,其中红色线条是 staircase=False,即指数型下降曲线,蓝色线条是 staircase=True,即阶梯式下降曲线
该衰减方法的优点是收敛速度较快,简单直接。
piecewise_constant
piecewise_constant(x, boundaries, values, name=None)
分段常数下降法类似于 exponential_decay 中的阶梯式下降法,不过各阶段的值是自己设定的。
其中,x 即为 global step,boundaries=[step_1, step_2, ..., step_n] 定义了在第几步进行 lr 衰减,values=[val_0, val_1, val_2, ..., val_n] 定义了 lr 的初始值和后续衰减时的具体取值。需要注意的是,values 应该比 boundaries 长一个维度。
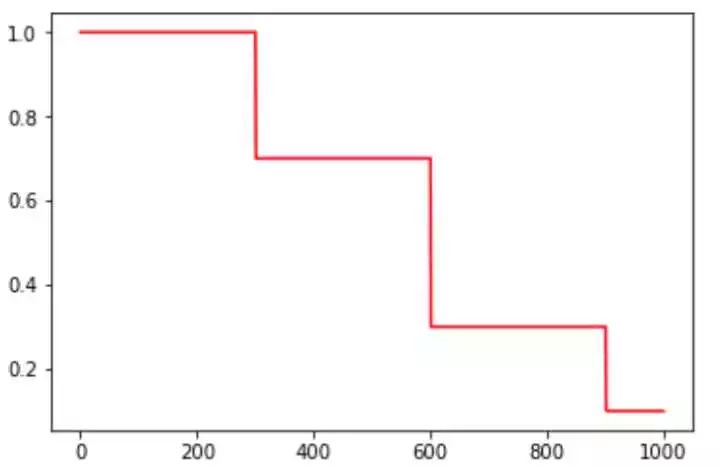
图 2. piecewise_constant 示例
这种方法有助于使用者针对不同任务进行精细地调参,在任意步长后下降任意数值的 learning rate。
polynomial_decay
polynomial_decay(learning_rate, global_step, decay_steps,
end_learning_rate=0.0001, power=1.0,
cycle=False, name=None)
polynomial_decay 是以多项式的方式衰减学习率的。
It is commonly observed that a monotonically decreasing learning rate, whose degree of change is carefully chosen, results in a better performing model.
This function applies a polynomial decay function to a provided initial `learning_rate` to reach an `end_learning_rate` in the given `decay_steps`.
其下降公式也在函数注释中阐释了:
global_step = min(global_step, decay_steps)
decayed_learning_rate = (learning_rate - end_learning_rate) *
(1 - global_step / decay_steps) ^ (power) + end_learning_rate
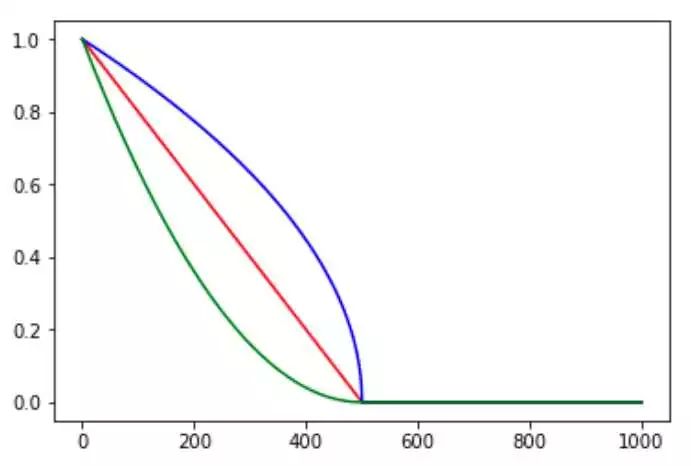
图 3. polynomial_decay 示例,cycle=False,其中红色线为 power=1,即线性下降;蓝色线为 power=0.5,即开方下降;绿色线为 power=2,即二次下降
cycle 参数是决定 lr 是否在下降后重新上升的过程。cycle 参数的初衷是为了防止网络后期 lr 十分小导致一直在某个局部最小值中振荡,突然调大 lr 可以跳出注定不会继续增长的区域探索其他区域。
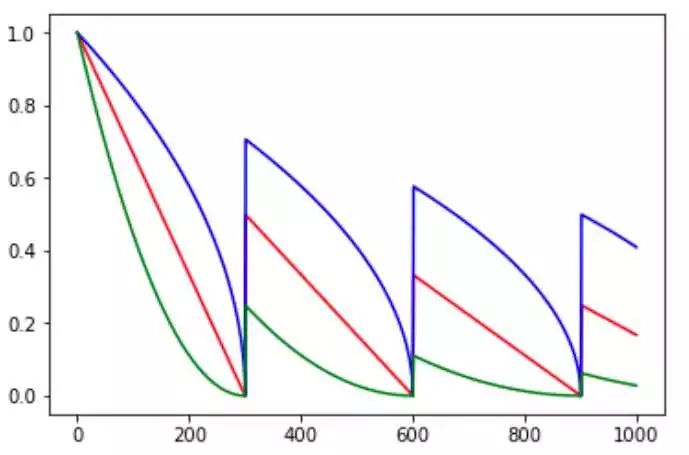
图 4. polynomial_decay 示例,cycle=True,颜色同上
natural_exp_decay
natural_exp_decay(learning_rate, global_step, decay_steps, decay_rate,
staircase=False, name=None)
natural_exp_decay 和 exponential_decay 形式差不多,只不过自然指数下降的底数是
exponential_decay:
decayed_learning_rate = learning_rate * decay_rate ^ (global_step / decay_steps)
natural_exp_decay:
decayed_learning_rate = learning_rate * exp(-decay_rate * global_step / decay_steps)
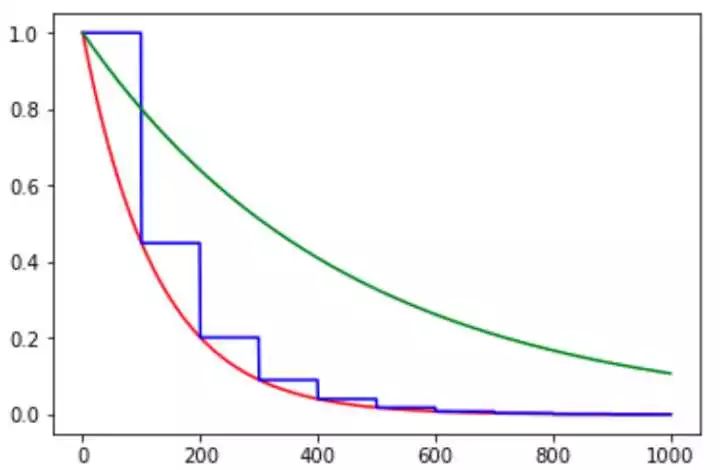
图 5. natural_exp_decay 与 exponential_decay 对比图,其中红色线为 natural_exp_decay,蓝色线为 natural_exp_decay 的阶梯形曲线,绿线为 exponential_decay
由图可知,自然数指数下降比 exponential_decay 要快许多,适用于较快收敛,容易训练的网络。
inverse_time_decay
inverse_time_decay(learning_rate, global_step, decay_steps, decay_rate, staircase=False, name=None)
inverse_time_decay 为倒数衰减,衰减公式如下所示:
decayed_learning_rate = learning_rate / (1 + decay_rate * global_step / decay_step)
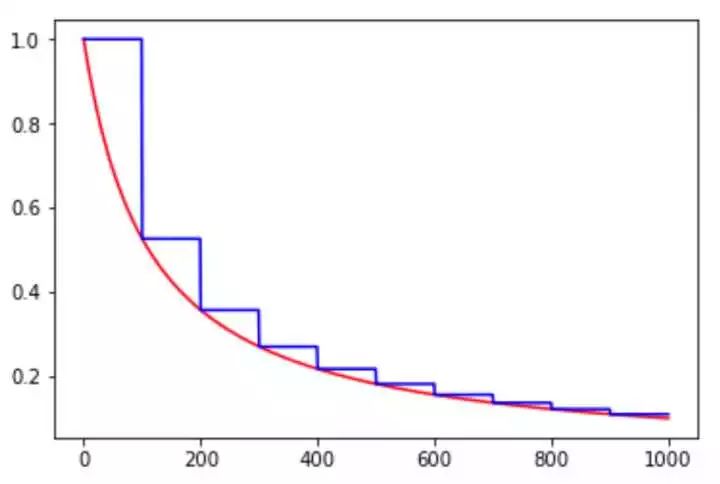
图 6. inverse_time_decay 示例
以上几种衰减方式相差不大,主要都是基于指数型的衰减。个人理解其问题在于一开始 lr 就快速下降,在复杂问题中可能会导致快速收敛于局部最小值而没有较好地探索一定范围内的参数空间。
cosine_decay
cosine_decay(learning_rate, global_step, decay_steps, alpha=0.0, name=None)
cosine_decay 是近一年才提出的一种 lr 衰减策略,基本形状是余弦函数。其方法是基于论文实现的:SGDR: Stochastic Gradient Descent with Warm Restarts(https://arxiv.org/abs/1608.03983 )
计算步骤如下:
global_step = min(global_step, decay_steps)
cosine_decay = 0.5 * (1 + cos(pi * global_step / decay_steps))
decayed = (1 - alpha) * cosine_decay + alpha
decayed_learning_rate = learning_rate * decayed
alpha 的作用可以看作是 baseline,保证 lr 不会低于某个值。不同 alpha 的影响如下:
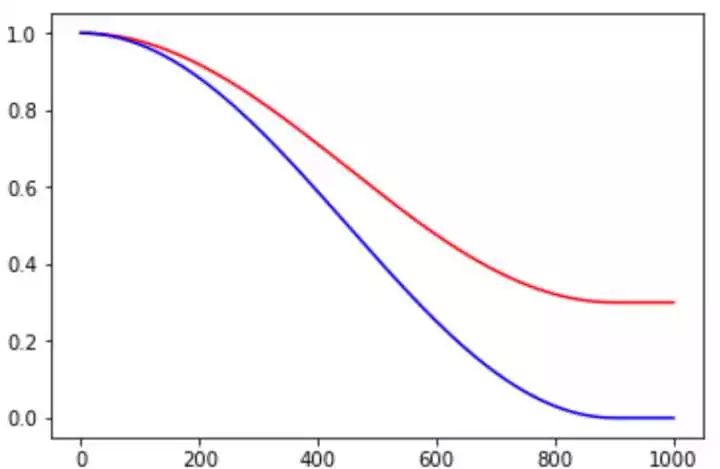
图 7. cosine_decay 示例,其中红色线的 alpha=0.3,蓝色线的 alpha=0.0
cosine_decay_restarts
cosine_decay_restarts(learning_rate, global_step, first_decay_steps,
t_mul=2.0, m_mul=1.0, alpha=0.0, name=None)
cosine_decay_restarts 是 cosine_decay 的 cycle 版本。first_decay_steps 是指第一次完全下降的 step 数,t_mul 是指每一次循环的步数都将乘以 t_mul 倍,m_mul 指每一次循环重新开始时的初始 lr 是上一次循环初始值的 m_mul 倍。
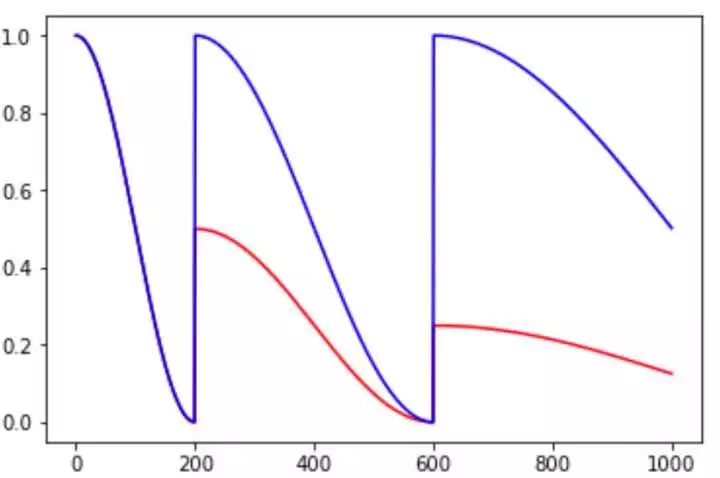
图 8. cosine_decay_restarts 示例,红色线条 t_mul=2.0,m_mul=0.5,蓝色线条 t_mul=2.0,m_mul=1.0
余弦函数式的下降模拟了大 lr 找潜力区域然后小 lr 快速收敛的过程,加之 restart 带来的 cycle 效果,有涨 1-2 个点的可能。
linear_cosine_decay
linear_cosine_decay(learning_rate, global_step, decay_steps, num_periods=0.5, alpha=0.0, beta=0.001, name=None)
linear_cosine_decay 的参考文献是 Neural Optimizer Search with RL(https://arxiv.org/abs/1709.07417 ),主要应用领域是增强学习领域,本人未尝试过。可以看出,该方法也是基于余弦函数的衰减策略。
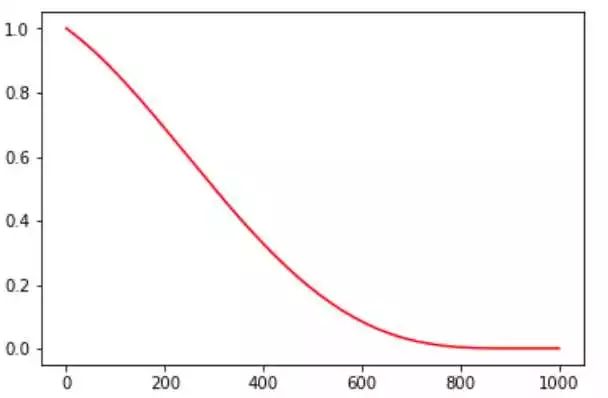
图 9. linear_cosine_decay 示例
noisy_linear_cosine_decay
noisy_linear_cosine_decay(learning_rate, global_step, decay_steps,
initial_variance=1.0, variance_decay=0.55,
num_periods=0.5, alpha=0.0, beta=0.001,
name=None)
参考文献同上。该方法在衰减过程中加入了噪声,某种程度上增加了 lr 寻找最优值的随机性和可能性。
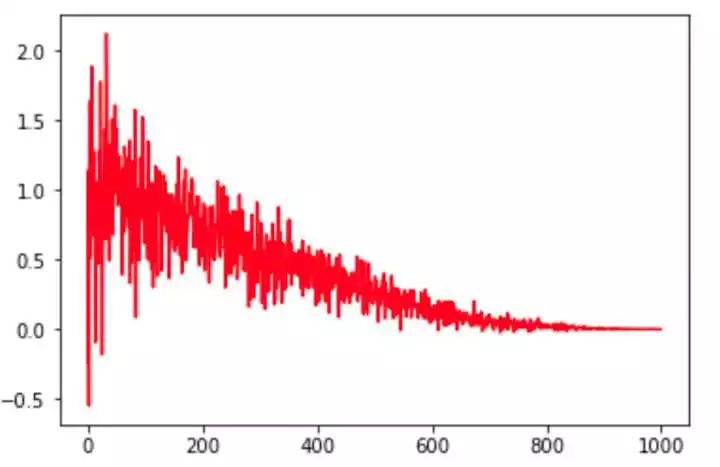
图 10.noisy_linear_cosine_decay 示例
auto_learning_rate_decay
当然大家还可以自定义学习率衰减策略,如设置检测器监控 valid 的 loss 或 accuracy 值,若一定时间内 loss 持续有效下降/acc 持续有效上升则保持 lr,否则下降;loss 上升/acc 下降地越厉害,lr 下降的速度就越快等等自适性方案。
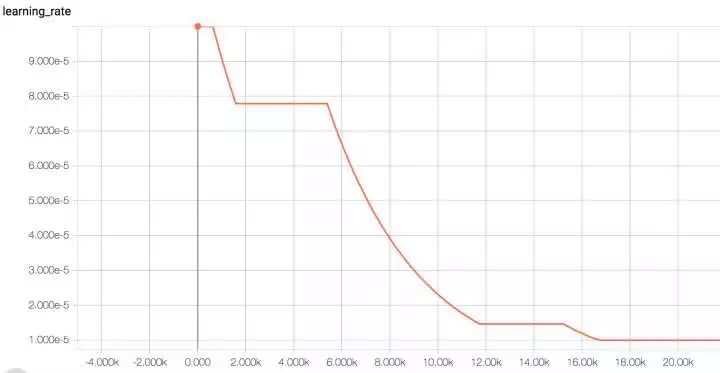
图 11. auto_learning_rate_decay 效果示例
最后,祝大家炼丹愉快!
CCF ADL 系列又一诚意课程
两位全球计算机领域 Top 10 大神加盟
——韩家炜 & Philip S Yu
共 13 位专家,覆盖计算机学科研究热点
▼▼▼
新人福利
关注 AI 研习社(okweiwu),回复 1 领取
【超过 1000G 神经网络 / AI / 大数据,教程,论文】
为什么说随机最速下降法 (SGD) 是一个很好的方法?
▼▼▼




