Circle Loss之一：Unified Loss是如何统一的？

会员服务 ·

Circle Loss之一：Unified Loss是如何统一的？

2020 年 5 月 8 日 CVer

点击上方“CVer”，选择加"星标"或“置顶”

重磅干货，第一时间送达

本文转载自：Ziyi的偏见

CVPR2020，来自旷视孙奕帆，瑞斯派克特

https://arxiv.org/abs/2002.10857

摘要：

研究领域是深度特征学习（deep feature learning），领域内研究目的是最小化类间相似度（，similarity of negative pairs)以及最大化类内相似度（，similarity of positive pairs）。调研发现主流的度量学习（甚至多分类学习）损失函数都会归为，作者观察到这样的损失对于所有的样本相似度产生的惩罚是一致的，无论他们的对应关系如何。故而一个比较好的思路是，对于那些更远离最优解的点进行更多惩罚（相应的更近的点惩罚更少）

intro简单：

提出关于深度特征学习的两条路子：类别标签以及样本对应关系标签。但殊途同归都会归结到同一个优化目标的变种：，使用这样的损失函数会带来两个明显的问题：

对于和相同的惩罚力度，举例来说，当已经接近0但还很小的时候，虽然直觉上需要对更多关注，但依然会给和相同尺度的关注。
优化的目标往往会得到一个分类边界，而该分类面会带来模糊性（模棱两个），举例来说，两个样本获得的<>分别是<0.7, 0.4> <0.5, 0.2>，他们都有，但是前者的和后者的仅有0.1的差距。这种模糊性会对特征空间的可分离性造成较大影响。

尝试解决上面问题1，比较好的思路是分别对和添加权重和，优化目标变成了；同时将和分别设为和的线形相关项，举例来说：取和的最优目标为和，设定 , 。那么优化目标可以转化为，在这种情况下，分类面为，不难推测几何上是个圆。

相比与之前的研究，作者列举了三个circle loss和之前损失函数不同的点：

一种统一的深度特征学习损失（统一class label 和 pairwise label）；
灵活的优化方向（相比sn-sp对于两者相同的惩罚）；
确定的收敛状态，对于特征的可区分性有裨益。

本文先讨论文章中提出的Unified Loss（统一的深度特征学习损失），介绍上面提到的传统两条路子里的经典损失函数，并推导Unified Loss是如何将他们统一的。关于Circle Loss的主体将在接下来的文章里介绍。

两条路子

文中提到了进行深度特征学习的两条经典路子：给定类别标签 vs 给定成对标签，下面首先对这两条路子里比较经典的损失函数进行介绍。

给定类别标签的损失

Softmax

初始的softmax损失函数表达为：。其中代表的是最后一层softmax前网络生成的特征，就是第i个样本的特征；而代表的是softmax层矩阵第类对应的向量（可以视为第类特征的标的）。

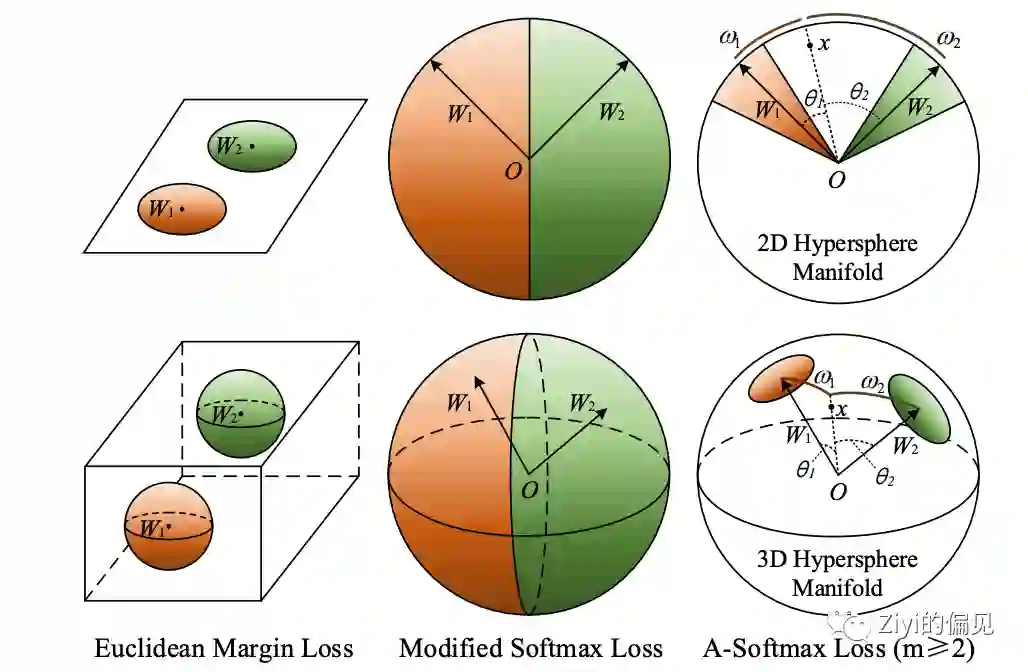
A-Softmax

首先对上面的式子进行了约束，使，那么修改后的的softmax损失变成了，不难分析，对应第j类特征的标的向量，主要判断该情况下与哪个方向更接近。

举二分类的例子，可视为在圆上的两个半圆，这种情况下分类边界并未直接拉开，直接比较和的大小；为了取得更分离的分类边界，取分类标准为以及 , 这样得到的分类边界不再紧贴，而在完美情况下有（代表的是）的角距离（这里可以考虑将W1和W2之间的夹角均分为m+1份，而分类边界分别为最接近W1和W2的一份，故而分类边界之间的角距离为），实现更好的可区分性，如下图的右三中两个分类区域之间的夹角。

拓展进多分类并对上面的，得到

，

其中有约束（余弦函数在[0,pi] 区间上成单调递减）。这个约束项在神经网络优化中很难保证，故而将上式中的余弦函数替换为关于的单调递减函数，使其在上述区间上和余弦函数表现一致，但定义域可以拓展。得到

，其中，

m是一个直接控制分类边界距离的量，当其取1时A-Softmax就回归到正常的Softmax，而m越大则对于分类边界距离的要求越高。

AM-Softmax

相比A-Softmax里只对W进行归一化处理，这里更进一步，将得到的特征f也进行归一化处理，即，得到在上面的变种。相对于A-Softmax中对分类面的方式，AM-Softmax采用了更为直观的方法，直接取在余弦函数（对特征和矩阵进行归一化后余弦函数可以直接理解为相似度）后增加边界，即取分类面（正类为1的情况下）。对应的AM-Softmax损失函数为

这里只有一个超参作为权重，虽然前作中都有设置其为可学习的超参，但实验发现收敛很慢且在学习过程中并不会变大，故而直接将其固定为一个较大的值（30）。这里先给出一张关于AM-Softmax对比原Softmax损失和其变种的直观图（其中SphereFace就是之前介绍的A-Softmax）。可以比较明显的看到，AM-Softmax在s=10,m=0.2的情况下以及高比较接近A-Softmax所取得的结果，而调整更大的m可以得到更有区分性的结果。

关于A-Softmax和AM-Softmax之间的区别，这里说一下自己的理解，大致上有两点：

优化目标上，A-Softmax依然是关于进行优化，包括对分类边界的约束也是加在上，利用余弦函数在一定区间上的单调递减使不同类之间的分类边界有分隔；而AM-Softmax则是直接对余弦函数进行优化，并直接把边界放在了余弦函数上。
对于分类边界的控制参数m，A-Softmax通过调大m来使分类边界之间的距离(通过控制中的前一项)变大，但并无法直接控制使分类边界更宽；AM-Softmax调大m则非常直观，对应了调大分类边界之间的角度（）。

给定成对标签的损失

Contrastive Loss

对比损失，更像是在给定成对标签情况下对softmax的直接修改，其损失函数如下。

其中依然代表网络得到的第i个样本的特征，sim函数为任意相似度度量函数（可以直接带入余弦函数），为i同类(positive)的样本，而下面分母中为第k个与i不同类(negative)的样本。根据softmax，不难推测这样的对比损失就是将问题转化为多分类问题，使同类间样本更像而非同类间样本更远。

Triplet Loss

挖坟才知道triplet loss这文章已经是15年的文章，与上面的对比损失一样，均选择数个与当前样本同类和异类的样本进行特征抽取，其定义如下。

其中和的定义和对比损失一致，并对做了归一化，使其范数为1。虽然文中选择了用L2距离作为相似度衡量（相似度度量距离降低而降低），使不相似类间的距离更大而相同类间的距离更小，但依然可以采用余弦函数这种相似度度量随距离降低而升高的相似度衡量方法，在这种情况下（以余弦函数举例）上述triplet loss可以改写为如下的式子（考虑f已经归一化，故而两个f的内积即为其夹角的余弦）：

统一的损失函数

这里给出作者提出的一种统一化的损失函数（Unified Loss），定义如下

其中，与分别代表同类样本和不同类样本的相似度，L和K分别表示有K个同类样本对和L个不同类样本对，m则依然代表着类别间隔。虽然文中也大致描述了上述Unified Loss如何转变为使用类别标签的损失函数和使用成对标签的损失函数，我在阅读的时候还是遇到了一些障碍，所以把我理清的过程也写在这里。需要声明，特别感谢一位王峰师兄，上述AM-Softmax的工作是他的工作，他在关于circle loss问答下的解答对我理解帮助非常大(也成为了度量学习话题下的最多赞答案)，涉及优化转变的部分都是他的回答帮助了我。

1. 针对给定类别标签的情况

首先对特征进行归一化处理，并使用余弦函数作为上述相似性度量，那么unified loss就转化为

；

这时只取一个正样本对，即K=1，那么损失函数再次转变为下面的形式，可以直接得到AM-Softmax：

再继续转化下去，取并使m=0，将余弦函数写成内积的形式，直接变成了softmax函数。

2. 针对给定成对标签的情况

需引入两点：

Softplus函数是对Relu的平滑近似：
LogSumExp是对max函数的平滑近似：

在这两点的基础上，对Unified Loss进行下面变换

这样就实现了从 Unified Loss到Triplet Loss的转化（并且是hard-mining）。

最后提一嘴，这文章一开始写在知乎专栏上（名字是一样的），微信公众号对公式的友好度并不很高，可以顺道移步帮点波赞

https://zhuanlan.zhihu.com/p/138356112

论文下载

在CVer公众号后台回复：0508，即可下载本论文

重磅！CVer-论文写作与投稿 交流群已成立

扫码添加CVer助手，可申请加入CVer-论文写作与投稿 微信交流群，目前已满1400+人，旨在交流顶会（CVPR/ICCV/ECCV/ICML/ICLR/AAAI等）、顶刊（IJCV/TPAMI/TIP等）、SCI、EI等写作与投稿事宜。

同时也可申请加入CVer大群和细分方向技术群，细分方向已涵盖：目标检测、图像分割、目标跟踪、人脸检测&识别、OCR、姿态估计、超分辨率、SLAM、医疗影像、Re-ID、GAN、NAS、深度估计、自动驾驶、强化学习、车道线检测、模型剪枝&压缩、去噪、去雾、去雨、风格迁移、遥感图像、行为识别、视频理解、图像融合、图像检索、论文投稿&交流、PyTorch和TensorFlow等群。

一定要备注：研究方向+地点+学校/公司+昵称（如论文写作+上海+上交+卡卡），根据格式备注，可更快被通过且邀请进群