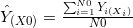数据分析师应该知道的16种回归技术：KNN回归

2018 年 8 月 6 日 数萃大数据

KNN是一种非常简单的机器学习算法，在数据分析中常用来对数据进行分类，而本文将介绍如何使用KNN进行回归。

介绍KNN回归前，我们先了解下分类和回归的区别是很有必要的。分类和回归是数据挖掘领域两个主要任务。分类和回归的区别在于输出变量的类型，分类是给定一个特定模型，根据训练集推断它所对应的类别；回归是给定一个特定模型，根据训练集推断它所对应的输出y（实数）是多少。预测明天的气温是多少度，这是一个回归任务；预测明天是阴、晴还是雨，就是一个分类任务。

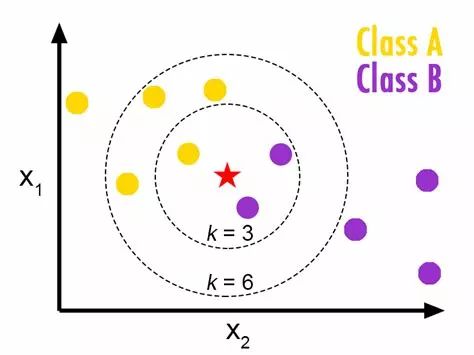
KNN算法的基本思路：一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别。下面通过一个简单的例子说明：如下图，红五角星属于哪一类，A还是B？如果K=3，由于B所占比例为2/3，因此红五角星属于B，如果K=6，由于A所占比例为2/3，因此红五角星属于A。因此K的选择很大程度上决定了KNN算法的结果。

上例留给我们两个问题：样本间距离的度量和K值的确定。根据变量类型的不同，样本间距离的测量方法也不同。

连续变量

离散变量

K值可以基于均方根误差(RMSE)确定，启发式地找到一个最优近邻数k。

KNN回归

KNN回归是基于距离确定回归的方法。给定一个K值和一个预测点X0，KNN回归首先确定K个距离X0最近的观察点，用N0来表示这些观察点，然后用N0中所有观察点对应的因变量值的均值来作为预测点X0的估计值。用公式表示

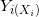
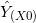
其中是N0中每个Xi所对应的值，X0是初始选择的预测点，是X0所对应的因变量的值。

KNN回归和线性回归可以通用有时又存在差异，前者是非参回归中较简单的一种方法，后者常用在参数回归中。那么对于一组数据，我们该如何选择是使用KNN回归还是线性回归呢？一般，当自变量个数小于3时，KNN方法能够显著减少误差，KNN方法能够提供更多的信息来进行回归，但随着变量逐渐增多，K个最近的观测值对应的因变量的均值可能会成倍的距离偏离实际的因变量的值，因此当变量多的时候，KNN效果就会逐渐降低。然而使用线性回归时，一般不受到变量个数的影响，因此变量多少，对残差的影响并不是很大。当预测变量或是自变量多于3或4时，尽量选择线性回归作为回归效果可能会更好些。

案例分析

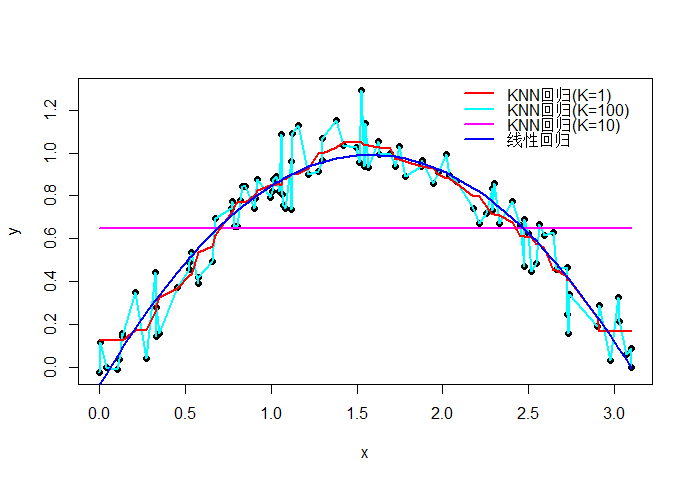
KNN回归在R中可以使用FNN::knn.reg实现，下面通过一个简单的例子说明，图中的黑色实心点表示样本观测值，红、天蓝、紫和蓝色曲线分别表示KNN(k=1,k=100,k=10)以及线性回归，经计算K=10时的RMSE为0.1035,而线性回归的RMSE为0.1055，因此KNN回归略优于线性回归，且从图中可以看出，KNN的拟合曲线更加灵活，能够包含更多的样本信息。

library(FNN)
x = runif(100,0,pi)
e = rnorm(100,0,0.1)
y = sin(x)+e
grid2=data.frame(x)
knn1 = knn.reg(train = x, test = grid2, y = y, k = 1)
knn10 = knn.reg(train = x, test = grid2, y = y, k = 10)
knn100 = knn.reg(train = x, test = grid2, y = y, k = 100)
plot(x,y,type = 'n')
points(x,y,pch=16,col='black')
ORD = order(grid2$x)
lines(grid2$x[ORD],knn1$pred[ORD],lwd=2,col=5)
lines(grid2$x[ORD],knn100$pred[ORD],lwd=2,col=6)
lines(grid2$x[ORD],knn10$pred[ORD],lwd=2,col=2)
coe=coef(lm(y~x+I(x^2)))
lines(x[ORD],coe[1]+coe[2]*x[ORD]+coe[3]*x[ORD]^2,
      lwd=2,col=4)
legend('topright',c('KNN回归(K=1)','KNN回归(K=100)',
                    'KNN回归(K=10)','线性回归'),bty='n',
       lty=1,lwd=2,col=c(2,5,6,4))