观点 | 从信息论的角度理解与可视化神经网络
选自TowardsDataScience
作者:Mukul Malik
机器之心编译
参与:Pedro、思源
信息论在机器学习中非常重要,但我们通常熟知的是信息论中交叉熵等模型度量方法。最近很多研究者将信息论作为研究深度方法的理论依据,而本文的目标不是要去理解神经网络背后的数学概念,而是要在信息论的视角下可视化与解读深度神经网络。
「Information: the negative reciprocal value of probability.」—克劳德 香农
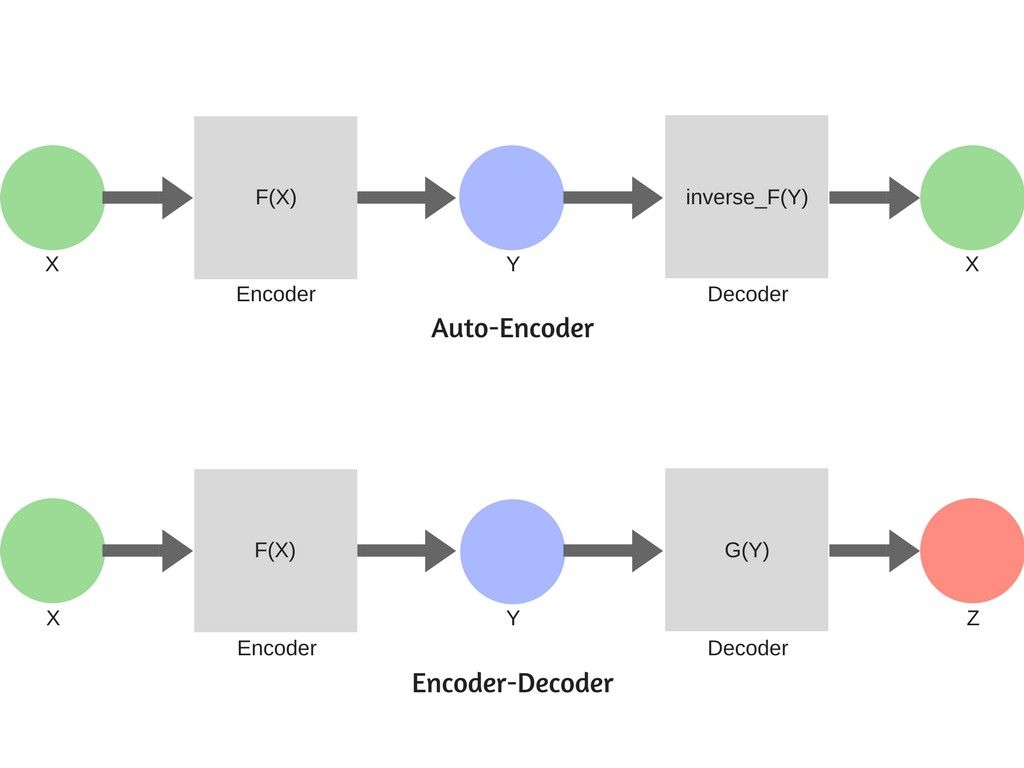
编码器-解码器
编码器-解码器架构绝不仅仅是组合在一起的两个卷积神经网络或者循环神经网络!事实上它们甚至都可以不是神经网络!
最初从信息论的概念来说,编码器仅仅用于压缩信息而解码器可以扩展编码过的信息(https://www.cs.toronto.edu/~hinton/science.pdf)。
而对于机器学习来说,解码和编码的过程都不是无损的,也就是说总有一些信息会丢失。编码器编码后的输出被称为上下文向量,同时它也是解码器的输入。
常用的编码器-解码器框架配置有两种:
解码器是编码器的逆函数。在这种设定下,解码器要尽可能地复原原始信息。它通常被用于数据去噪,这种设定有一个特殊的名字,叫做自编码器。
编码器是一个压缩算法而解码器是一个生成算法。它用来将上下文信息从一种格式转换到另一种格式。
应用示例:
自编码器:编码器把英文文本压缩成一个向量。解码器根据这个向量生成原始的英文文本。
编码器-解码器:编码器把英文文本压缩成一个向量。解码器根据这个向量生成原始英文文本的法语译文。
编码器-解码器:编码器把英文文本压缩成一个向量。解码器根据文本内容生成一幅图片。
信息论
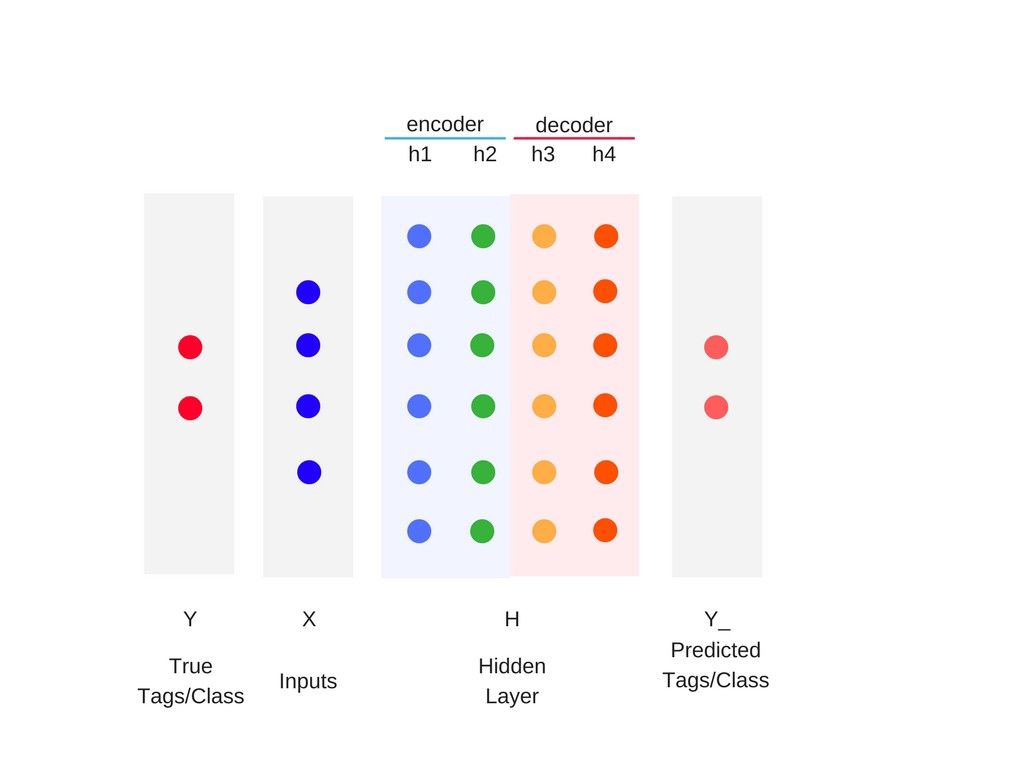
现在,如果我说每一个神经网络本身都是一个编码器-解码器框架;对大多数人来说,这听起来非常荒诞,但我们可以重新思考一下这个观点。
我们用 X 来表示输入层,用 Y 来表示(训练集中)真实的标签或者说类别。现在我们已经知道神经网络要寻找到 X 和 Y 之间潜在的函数关系。
因此 X 可以被视为 Y 的高熵分布。高熵是因为 X 除了 Y 的信息外还包含有许多其它的信息。
示例:
「这个男孩很棒」包含了足以让我们明白其包含「positive」情感信息(二元分类)。
但是,它也包含了如下的其它信息:
1. 这是一个特定的男孩
2. 这仅仅是一个男孩
3. 句子使用的时态是现在时
现在这句话低信息熵的表示可以为「positive」,而这同样也是输出信息,我们待会再来讨论这个问题。
现在想象一下每一个隐藏层都是一个单变量 H,这样多层网络就可以被表示为 H_0, H_1 ….. H_{n-1}。
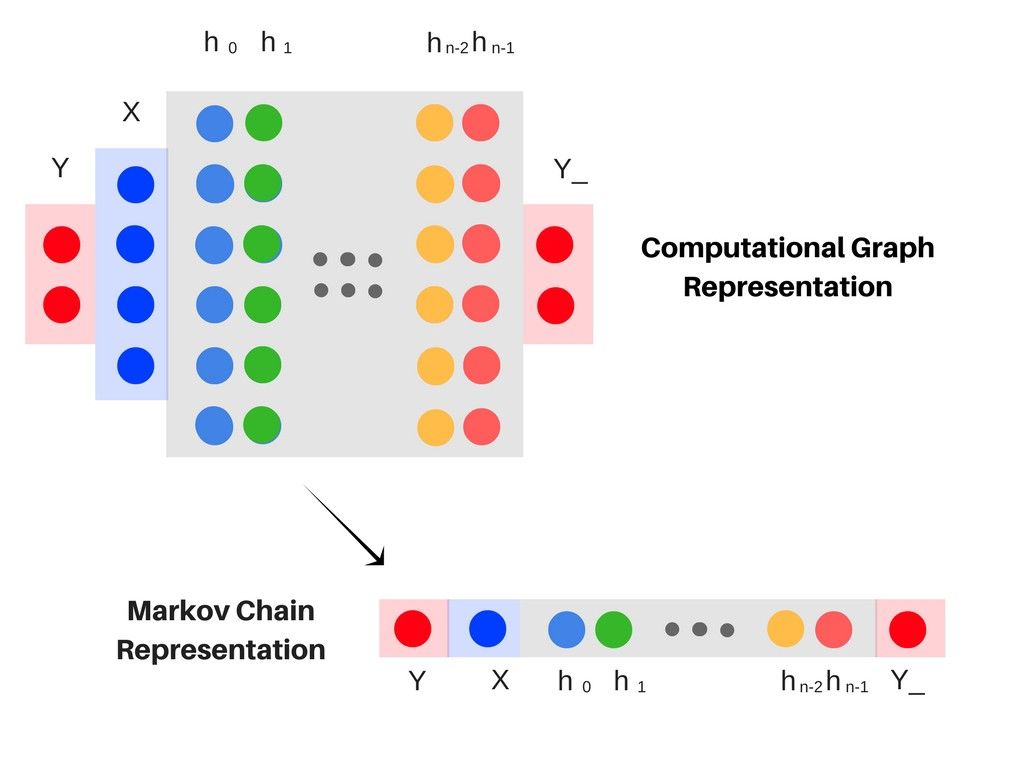
现在每一层都是一个变量,同时整个神经网络就变成了一个马尔科夫链,因为马尔科夫链中的每一个变量都仅仅依赖于前一个变量。
所以本质上来说每一个层都以不同的抽象形式构建不同部分的信息。
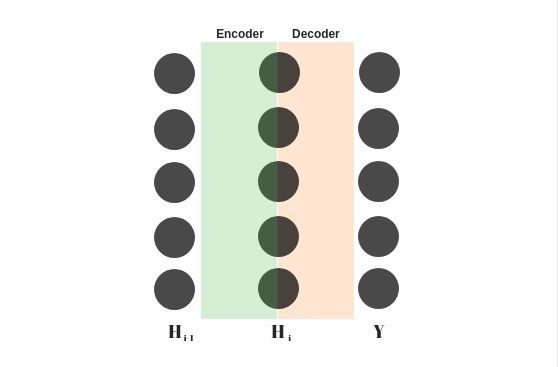
下图展示了以马尔科夫链的形式可视化神经网络。
最后一层 Y_ 应该产生一个低熵的结果(同最初的标签或者说类别'Y'相关)。
根据信息瓶颈理论,在获取 Y_ 的过程中,输入的信息 X 经过 H 个隐藏层的压缩最终保留同 Y 最相关的信息。
互信息
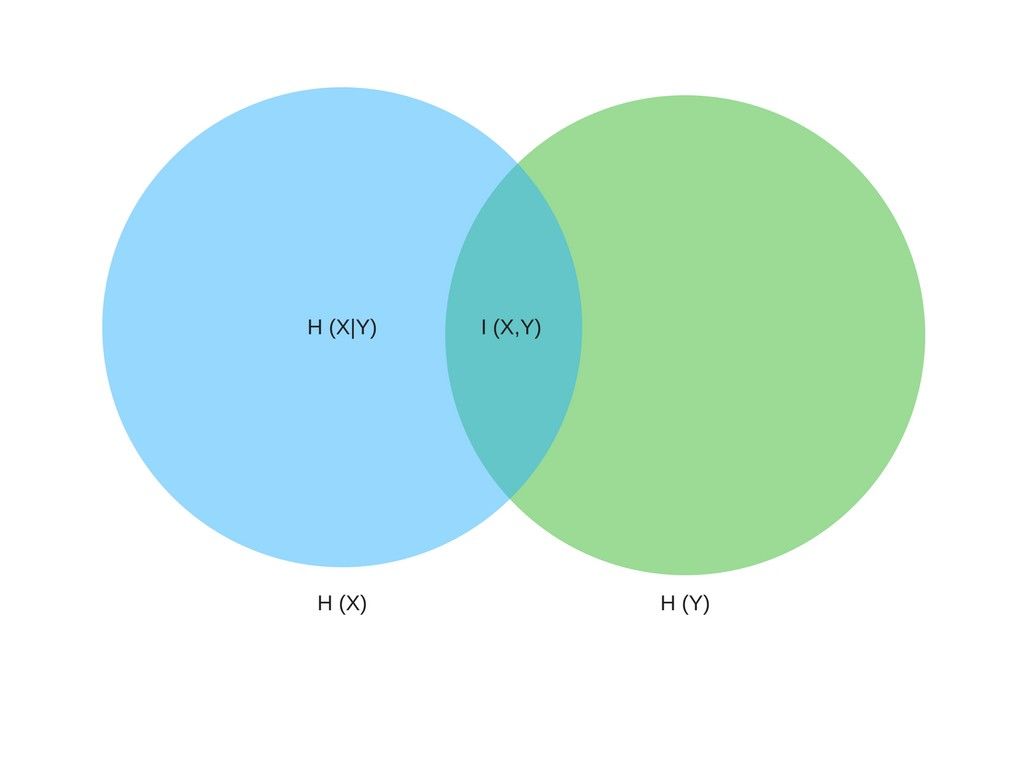
I(X,Y) = H(X)—H(X|Y)
如上所示为互信息的表达式,其中 H 代表信息熵,H(X) 代表变量 X 的信息熵。而 H(X|Y) 表示给定 Y 时 X 的条件熵,或 H(X|Y) 表明了在 Y 已知的情况下从 X 中移除的不确定性。
互信息的性质:
当信息沿着马尔科夫链移动时互信息只会减少。
对于再参数化来说互信息是恒定的,也就是说打乱一个隐藏层中的数值不会改变输出。
反思瓶颈
在神经网络的马尔科夫表达中,每一层都变成了部分信息。在信息论中,这些部分信息通常被视为是对相关信息的连续提炼。
另一个看待这个问题的视角是:输入先被编码然后被解码为输出。
那么,对于足够多的隐藏层:
神经网络采样的复杂度由最后一个隐藏层编码的互信息决定。
准确度由最后一个隐藏层解码后的互信息决定。
采样复杂度是模型为了达到一定程度的准确性所需要的训练样本数和种类。
训练阶段的互信息
我们计算了以下内容之间的互信息:
1. 隐藏层和输入
2. 隐藏层和输出
初始状态
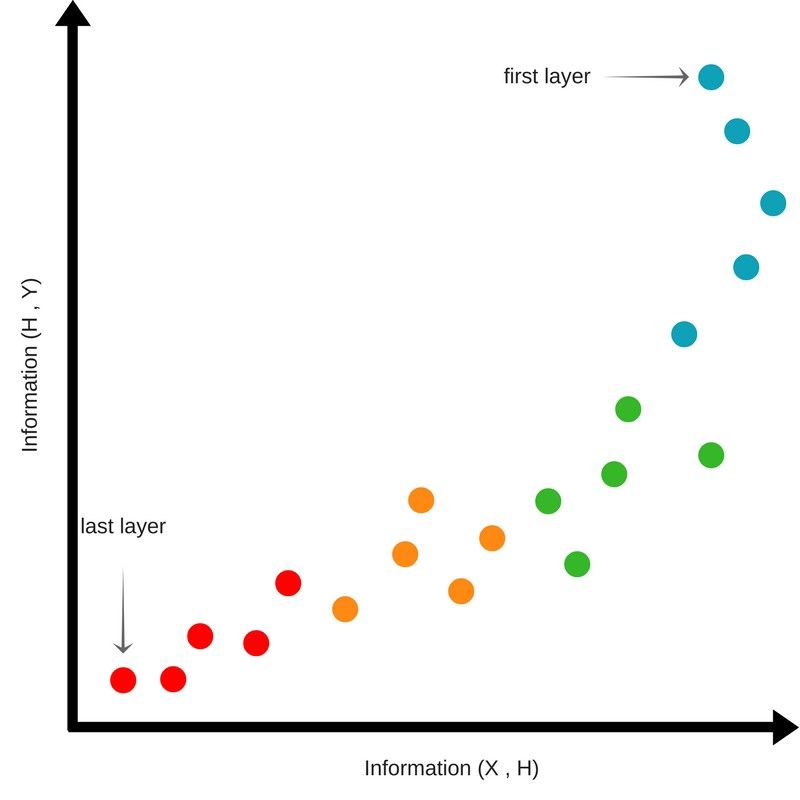
在一开始,我们随机初始化网络的权重。因此网络对于正确的输出一无所知。经过连续的隐层,关于输入的互信息逐渐减少,同时隐层中关于输出的信息也同样保持了一个相对比较低的值。
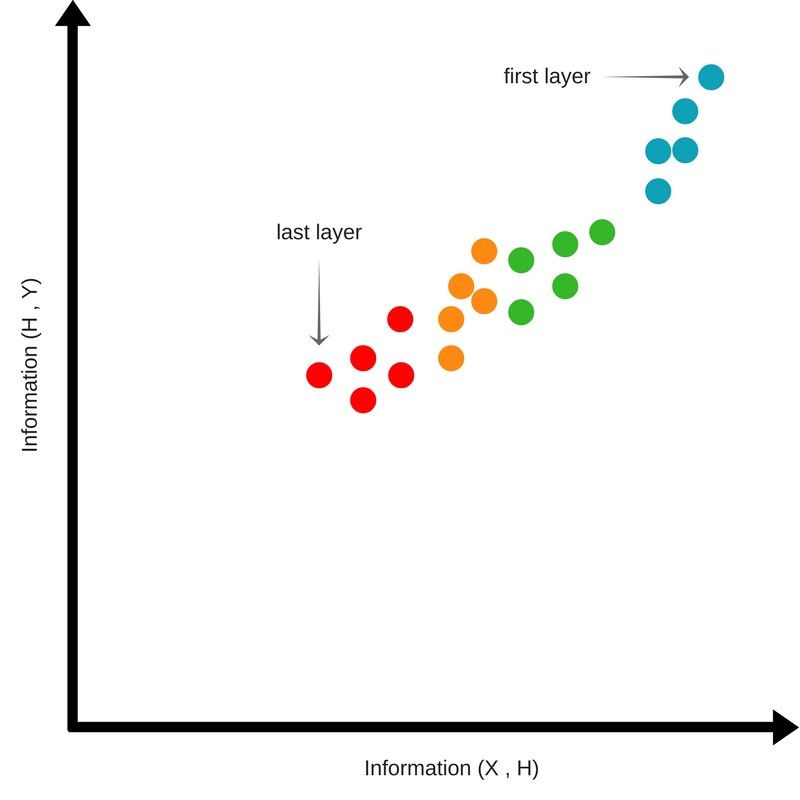
压缩阶段
随着训练的进行,上图中的点开始向上移动,说明网络获得了关于输出的信息。
但是上图的点同时也开始向右侧移动,说明靠后的隐层中关于输入的信息在增加。
训练阶段所需要的时间是最长。点的密度也需要最大化,上图的点最终都聚集在了右上角。这说明输入中同输出相关的信息得到了压缩。这被称为压缩阶段。
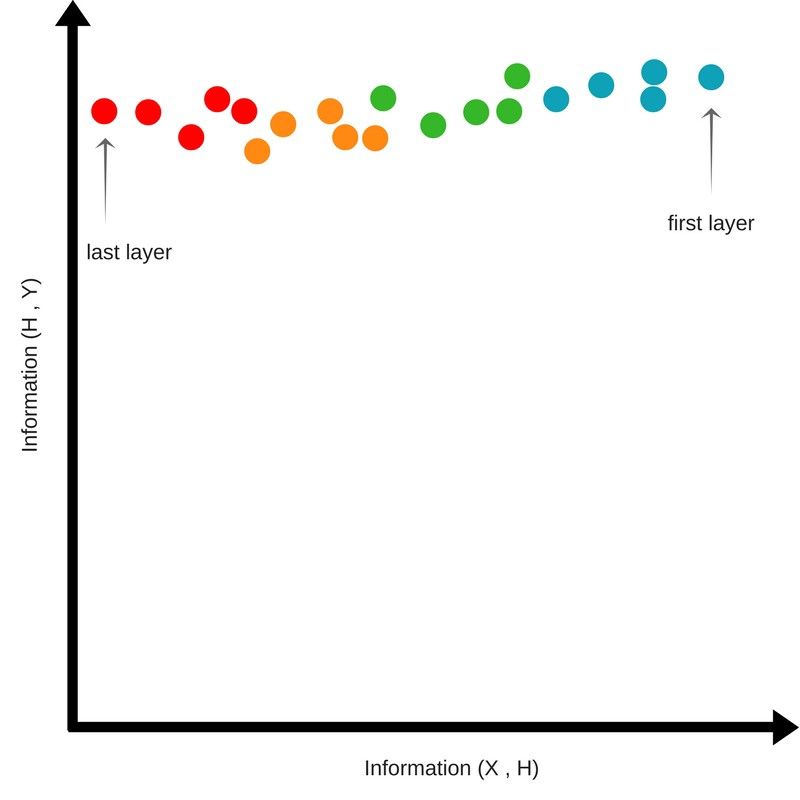
扩展阶段
在压缩阶段之后,点开始向上并且向左移动。
这说明经过连续的隐层后,神经网络丢失了一些输入信息,并且保留到最后一个隐层的内容是关于输出的最低熵信息。
可视化
马尔科夫链形式下的神经网络还说明:学习发生在隐层之间。一个隐藏层含有预测输出所需要的全部信息(包括一些噪声)。
因此我们可以使用每一层来预测输出,这帮助我们一窥这潜藏在所谓的黑箱中层与层之间的知识。
此外,这也能够让我们获知准确预测输出所需要的隐层数目。如果模型在较早的隐层中就已经饱和了,那么我们就可以裁剪或者丢弃掉接下来的隐层。
这些隐层通常有几百到几千不等的维度。受人类视觉系统进化本身所限,我们无法可视化超过 3 维的内容,因此我们使用了降维技术进行可视化。
我们有不同的方法来进行降维。Cristopher Olah 有一篇博客(http://colah.github.io/posts/2014-10-Visualizing-MNIST/)很好地阐释了这些方法。在这里我不会展开介绍 t-SNE 的细节,您可以在这篇博客(https://distill.pub/2016/misread-tsne/)中获得更多信息。
简单来说,t-SNE 试图通过保留高维空间中点在低维空间中近邻的方式来进行降维。因此它能够产生非常准确的二维和三维图像。
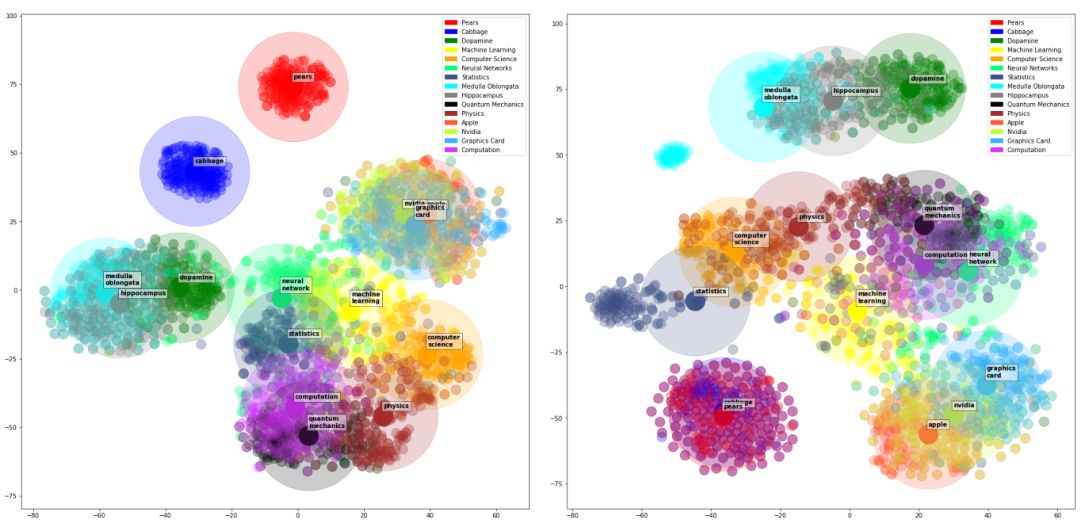
如下是一个有 2 个隐层的语言模型的层级图像。
关于这些图像:
挑选出 16 个单词
用最终的语言模型对每一个上述单词找到 N 个同义词(二维中 N=200,三维中 N=50)
得到每一个单词在每一层的向量表达
使用 t-SNE 得到上述单词向量的二维和三维的降维表达
画出降维后的表达
第一层和第二层的二维图。
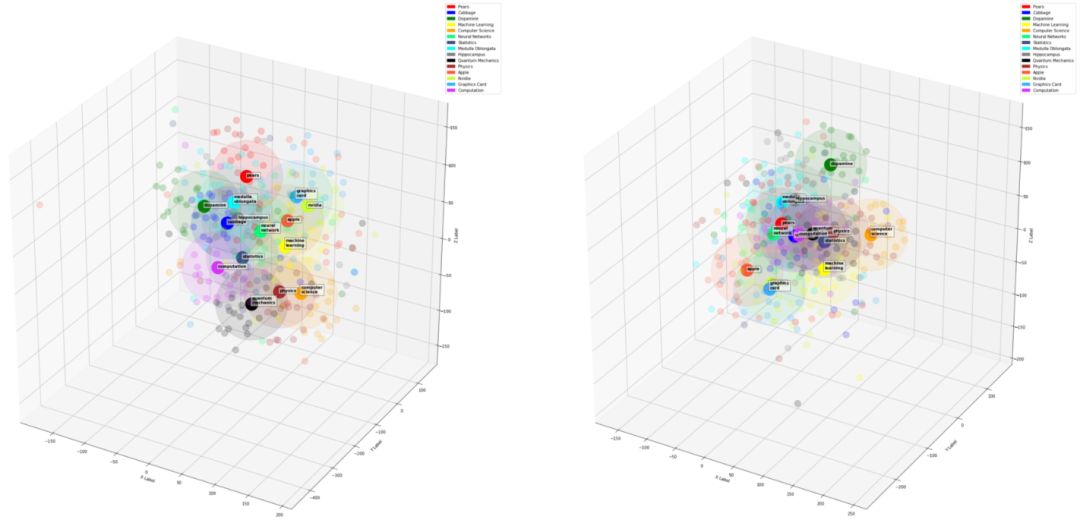
第一层和第二层的三维图。
总结
大多数的深度神经网络的工作原理都类似于解码器-编码器架构;
压缩阶段耗费了大部分的训练时间;
隐层的学习是自底向上的;
经过压缩阶段,神经网络丢弃掉的输入信息越多,输出结果就越准确(清除掉不相关的输入信息)。
本文为机器之心编译,转载请联系本公众号获得授权。
✄------------------------------------------------
加入机器之心(全职记者/实习生):hr@jiqizhixin.com
投稿或寻求报道:editor@jiqizhixin.com
广告&商务合作:bd@jiqizhixin.com