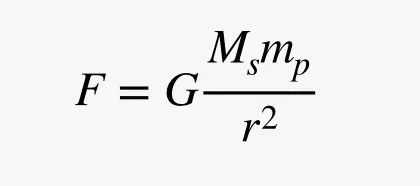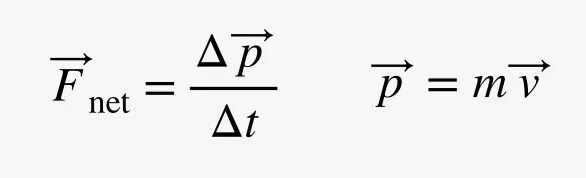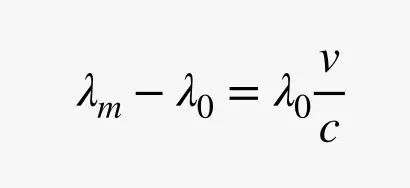手把手教你做出诺奖级研究：寻找系外行星（内附代码）

银河系之外的恒星在地球上看来不过是夜空中一个小小的亮点，直接观测围绕它们旋转的行星显然不可能。两位天文学家因发现第一颗系外行星获得了今年的诺贝尔物理学奖，不过这项工作背后的原理其实并不复杂……

图片来源：NASA

来源 Wired

撰文 Rhett Allain

翻译 张元一

编辑 戚译引

10 月 8 日，2019 年诺贝尔物理学奖将 2/3 授予米歇尔·马约尔（Michel Mayor）和迪迪埃·奎洛兹（Didier Queloz），以表彰他们在 1995 年做出的惊人发现：他们首次探测到一颗行星，围绕与太阳相似的遥远恒星运行。在此之前，我们所知的行星只有自己所处的太阳系中的八大行星。我们甚至都不知道行星在宇宙中是常见还是稀有，而这个问题有着重大的影响，它关乎外星生命存在的可能。

这是科学探索的壮举。马约尔和奎洛兹观察飞马座星系中的一颗恒星，叫做飞马座 51，距离我们 50.45 光年。我们可以看到恒星发出来的光，但是在那样的距离，光源的角度太小，望远镜无法分辨。换言之，我们看不到恒星本身。而且既然看不到恒星，那么我们当然也看不到环绕着它的小得多的行星。

那他们怎么做呢？当然是靠物理学了。与所有事物一样，理解它的最好方法是建立模型。因此，让我们构造一个有史以来被探测到的系外行星的简单模型。

飞马座 51 很像我们的太阳，只是更大一点；如果把它们放在一起，你很可能无法分辨谁是谁。而这颗行星被称为飞马座 51 b，和木星一样是个气态巨行星，离它的恒星近得不可思议，其轨道半径仅为 0.05 AU。（AU 代表天文单位，是从地球到太阳的平均距离。）作为对照，木星的轨道半径约为 5 AU。

现在我要倒推一下发现过程，当一回事后诸葛亮。我们将使用恒星和系外行星的估计质量以及轨道半径，来模拟该恒星-行星系统的行为，然后我会展示如何找到行星。当然，马约尔和奎洛兹得先从数据中得出这些估计值，但是他们脑海里很可能有相似的模型，来指导他们的工作。

在任何太阳系中都存在引力，将恒星和行星拉在一起。引力与两个物体的质量（分别记为 M_s 和 m_p）以及它们之间的距离（r）相关，其大小可通过这条公式得出：

这里，G 是引力常数，值为 6.67 x 10^-11 N×m²/kg²。作用在天体上的力实际上会产生什么影响呢？根据动量原理，它会改变其动量（p）——动量等于速度（v）乘以质量。像这样：

字母前的希腊符号 Δ 表示该变量的微小变化。变量上的箭头表明这些是矢量。听起来似乎很花哨，但它只是将方向信息添加到力和动量的大小中。我们需要知道事物的去向，不是吗？

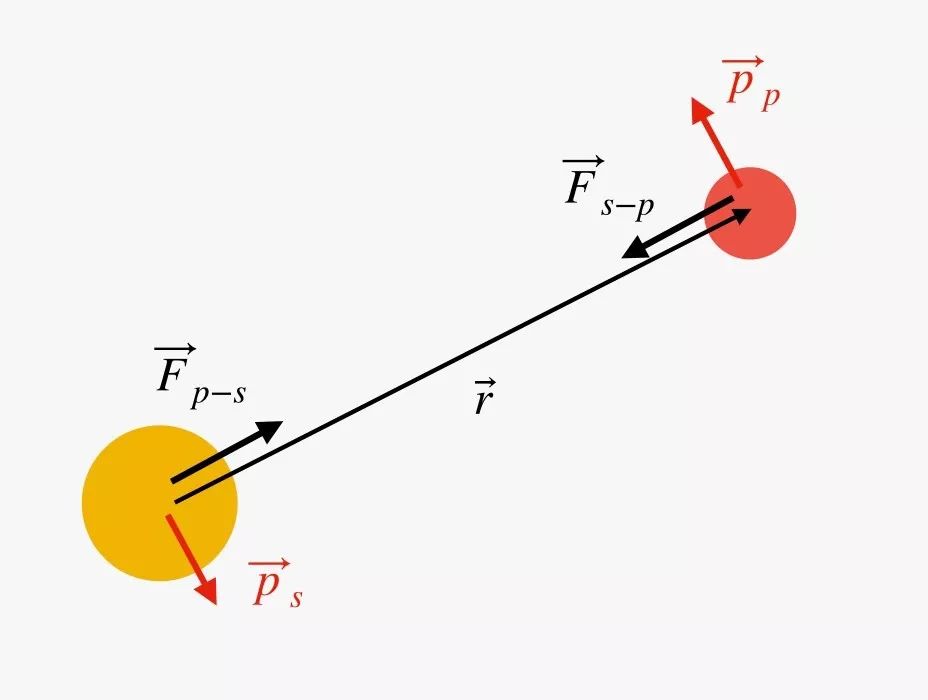
现在，为了画出该恒星-行星系统中的运动轨迹，我将使用逐步数值方法。上面的方程式表明了作用在恒星和行星上的力。由此，我可以计算出每个物体在一个很小的时间间隔（Δt）内的动量变化。然后我可以用那个来找到恒星和行星的新位置。这是力（F）及其动量变化（红色箭头）的示意图：

图片来源：Rhett Allain

“短”时间间隔到底有多长？飞马座 51 b 绕恒星一周只需要短短的四个地球日，这真是太快了。因此，我们尝试间隔 100 秒。然后，要绘制出一个完整的旋转轨迹，只需要重复这些力和动量计算 3000 次以上。哈！没问题，我可以将它们放在简短的 Python 脚本中进行迭代。

GlowScript 2.9 VPython

#Constants and stuff

G=6.67e-11

AU=1.496e11 #1 AU in meters

a=0.052*AU #semimajor axis

T=101.5388*3600 #orbital period in s

speed=136e3 #m/s

#m=jupiter/2

#r = 1.5*jupiter

Msun=1.9891e30

Rsun=695.5e6

Mjupiter=1.898e27

Rjupiter=69.911e6

mstar=1.11*Msun

rstar=1.237*Rsun

#Pegasi 51

star=sphere(pos=vector(0,0,0), radius=rstar,color=color.yellow)

star.m=mstar

placeholder=sphere(pos=vector(0,1.3*a,0),radius=1)

#Pegasi 51 b

planet=sphere(pos=vector(a,0,0),radius=1.5*Rjupiter,make_trail=True)

planet.m=1.5*Mjupiter

#set the initial momentum

planet.p=planet.m*vector(0,speed,0)

#make the total momentum zero

star.p=-planet.p

t=0

#time interval

dt=100

#do 10 orbits

while t<10*T:

  rate(250)

  #calculate the vector from star to planet

  r=planet.pos-star.pos

  #caclulate the gravitational force on planet

  F=-G*star.m*planet.m*r.hat/r.mag**2

  #update momentum of planet

  planet.p=planet.p+F*dt

  #update momentum of star (opposite force)

  star.p=star.p-F*dt

  #update position of star and planet

  planet.pos=planet.pos+planet.p*dt/planet.m

  star.pos=star.pos+star.p*dt/star.m

  t=t+dt

你也可以在这里查看代码：https://trinket.io/glowscript/f86aaefed6 

很明显，行星绕恒星运行，但是这里还发生着其他事情，只是在这种规模下看不到，那就是恒星也在移动！利用引力，恒星将经历与行星完全相同的动量变化。由于它具有更大的质量（p = m×v），因此它的速度变化要小得多，但它不是静止不动的。基本上，随着行星旋转，恒星会发生小幅度的摆动。

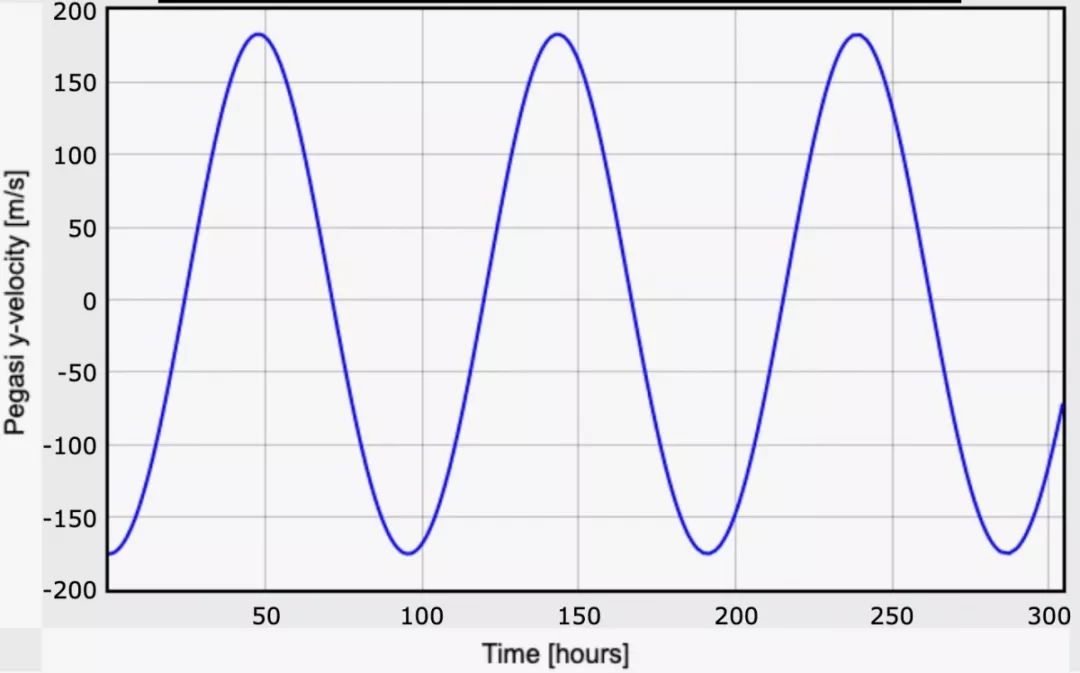
让我们详细解释一下：使用 Python 模型的结果，我将恒星的运动绘制在一维图上。（只是为了简单起见。假设一个三维空间中的 XYZ 坐标系，那么我只是在 y 方向上追踪其速度。）

画图代码参见：https://trinket.io/glowscript/f86aaefed6 | 图片来源：Rhett Allain

恒星的最大速度低于 200 m/s，其移动速度比行星慢得多，但它确实在移动。这是整个过程的关键。尽管看不到行星，但你可以看到行星对恒星速度的影响。再借助多普勒效应（Doppler effect），你可以通过观察星光来“观察”恒星的速度。

你很可能已经听说过多普勒效应了。当一辆飞速行驶的火车从你身旁飞过，或赛车在赛道上，听起来就像：

NEEEEEEEEEEEEEEEE-RAAAAAAAAAAAAAAAAR……

我不想再模仿一次了，总之这就是多普勒效应的标志性声音。当一个发声物体朝我们的方向移动时，我们会听到音调较高（即频率较高）的声音；当它经过并远离我们时，我们会听到音调较低的声音。

事实上，还存在光的多普勒效应。如果一颗星星向你移动，它的光将移向色谱的蓝色端（频率较高，或者说波长较短的一端）；当它远离你的时候，它的光将朝光谱的红色端（波长较长端）移动。

这很有用！由于我们已经知道光速 c（大约为3 x 10⁸ m/s），因此我们可以测量波长的偏移，并由此推断出恒星的速度。在这里，λ_m 是测得的波长，λ₀ 是假设它静止不动时你看到的波长。

但是，看看右边的表达式，你会发现一个问题。如果分子中物体的速度（v）比分母中的光速（c）小得多，那么得到的波长偏移会很小，而这正是飞马座 51 的情况。

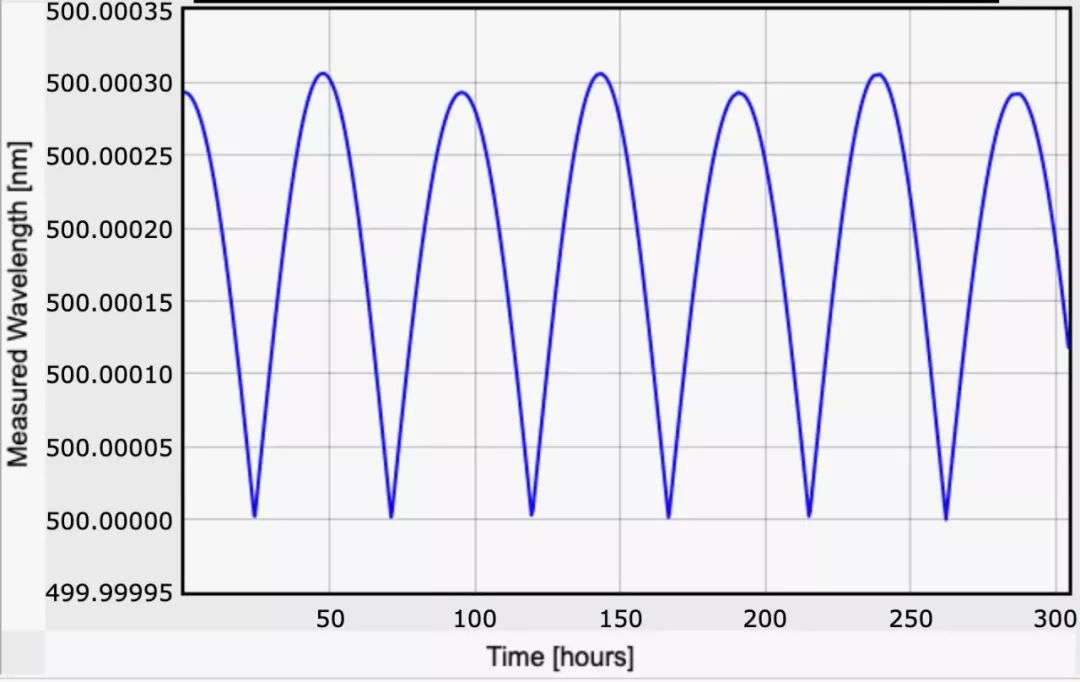
举个例子。假设这颗恒星发出的光波长为 500 纳米（相当于一米的五千亿分之一），这大致对应光谱上的绿色。使用这个波长和上述模型中恒星的速度，以下是测得的波长随时间变化的曲线图：

图片来源：Rhett Allain

这看起来仿佛是很大的波动，其实只是因为 y 轴上的刻度单位很小。仔细观察，你会发现波长范围在 500.00000 nm和 500.00031 nm 之间。这是一个极小的偏移，因此很难检测到。而且，情况还可能变得更糟！计算的假设前提是这颗恒星正在朝向或远离我们移动；但是如果行星轨道不一样，恒星相对于地球上下运动怎么办？那种情况下，我们看不到任何波长偏移。我们永远不会知道那里有一颗行星。

听起来很困难？现在你知道为什么这颗行星一直到 1995 年才被发现，以及为什么马约尔和奎洛兹能获得这样的荣誉了吧——诺贝尔奖委员会评价他们“开始了天文学的革命”。确实，利用他们开创的方法以及其他一些创新技术，天文学家已经在银河系中发现了 4000 多颗系外行星。也许其中一颗行星上也生活着杰出的科学家，谁知道呢？

本文来自微信公众号“科研圈”。如需转载，请在“科研圈”后台回复“转载”，或通过公众号菜单与我们取得联系。原始文章请点击“阅读原文”。

▽ 精彩回顾 ▽