顶会宠儿:几何深度学习是个啥?读完这篇,小白也可以了解GDL!
新智元报道
新智元报道
来源:paperspace
编辑:科雨、白峰
【新智元导读】如果有心,很容易感受到几何深度学习(尤其是图神经网络)在近两年的顶会中超高的存在感。那这一新兴热门领域和传统深度学习有何区别?当前热门应用又是哪些?这篇文章带你迈入几何深度学习(Geometric Deep Learning, GDL) 的大门。「新智元急聘主笔、高级主任编辑,添加HR微信(Dr-wly)或扫描文末二维码了解详情。」
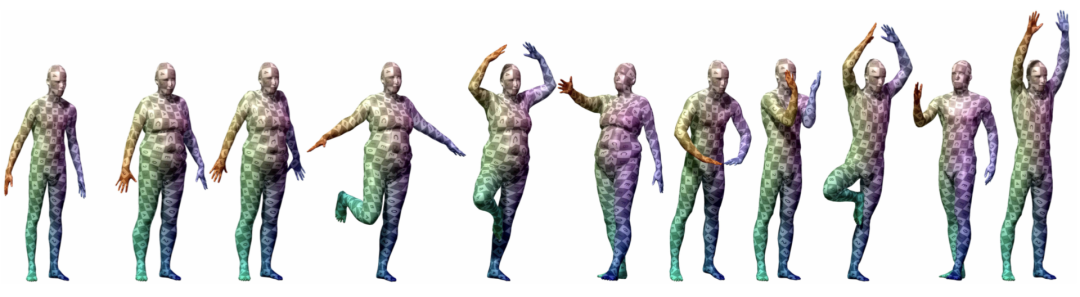
深度学习巨头LeCun牵头的几何深度学习在讲啥?
深度学习巨头LeCun牵头的几何深度学习在讲啥?
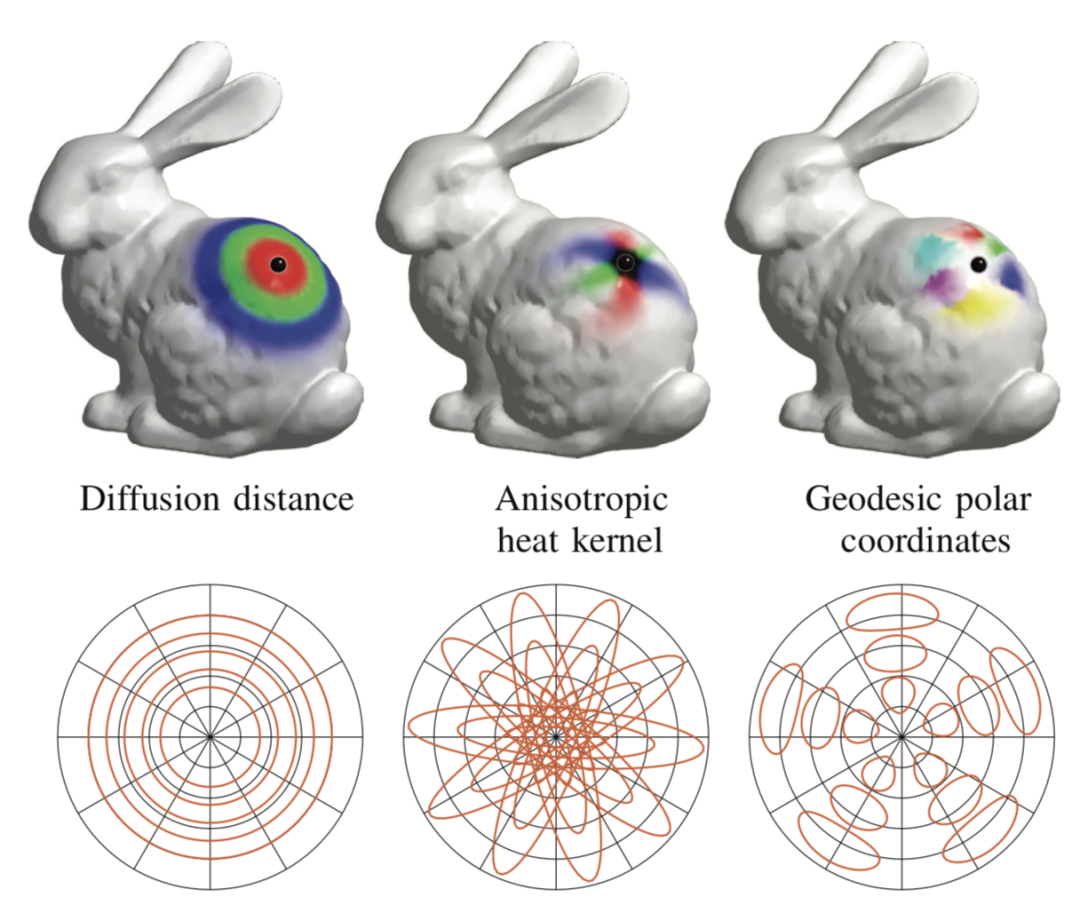
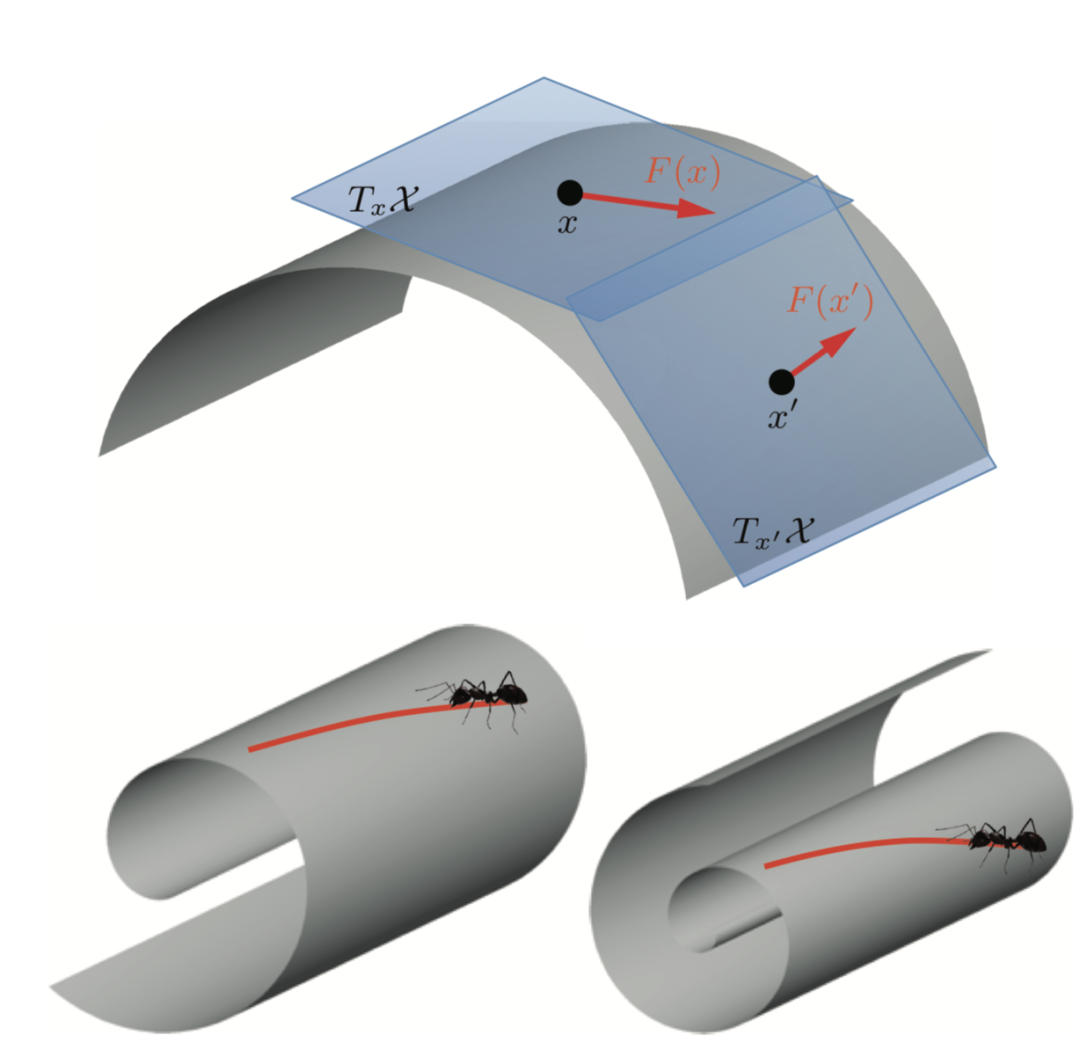
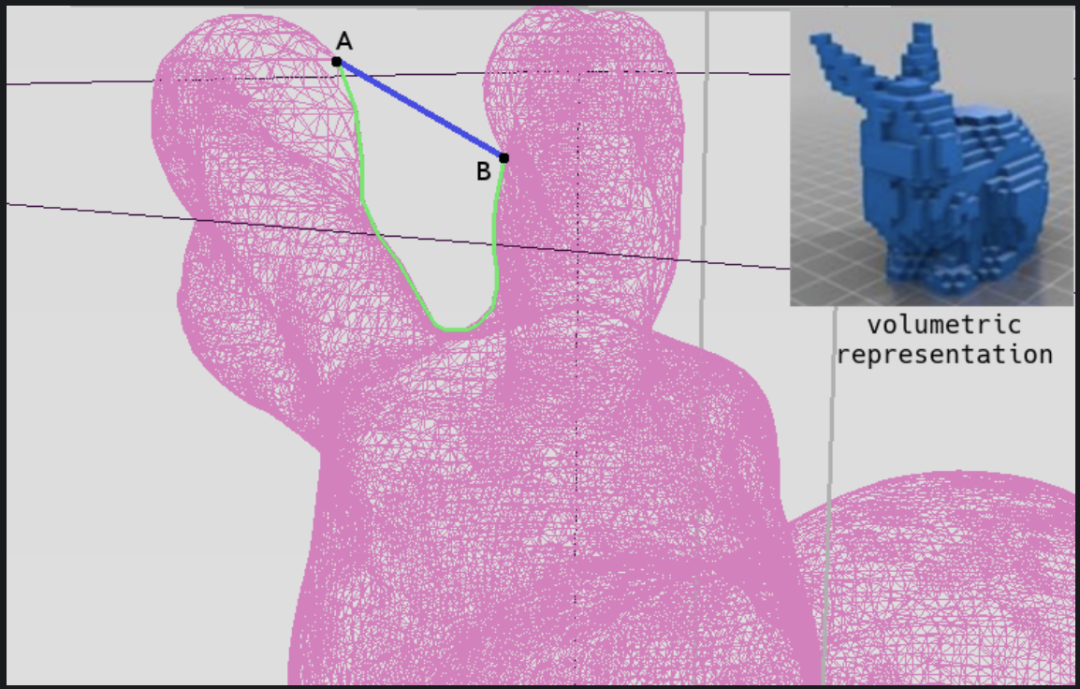



神经网络大比拼
神经网络大比拼
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
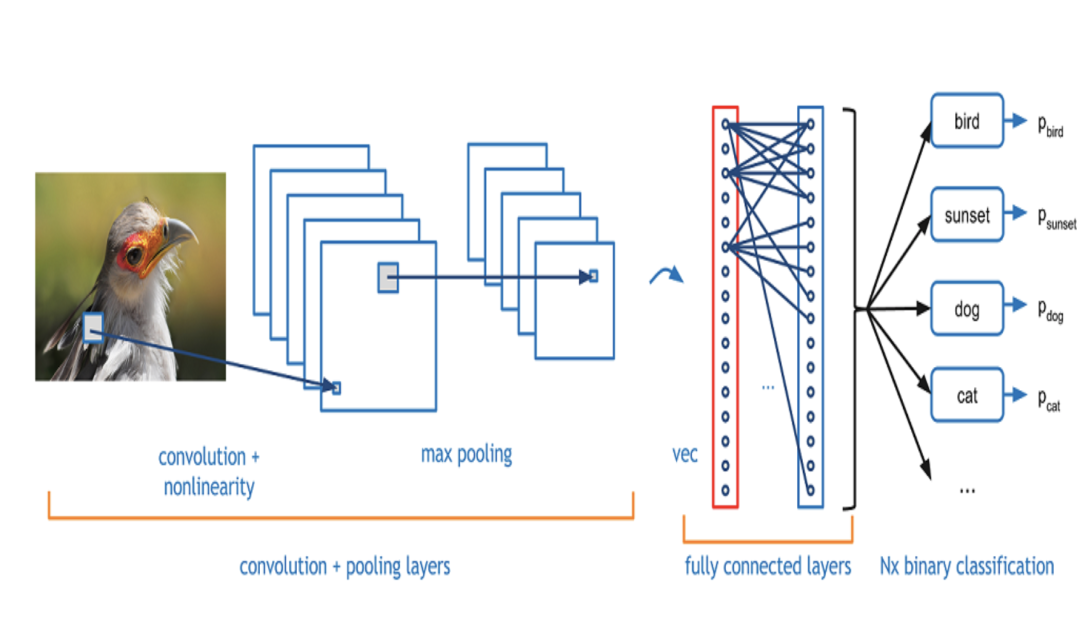
预测新冠发病率!几何深度学习要怎么玩?
预测新冠发病率!几何深度学习要怎么玩?
图分割

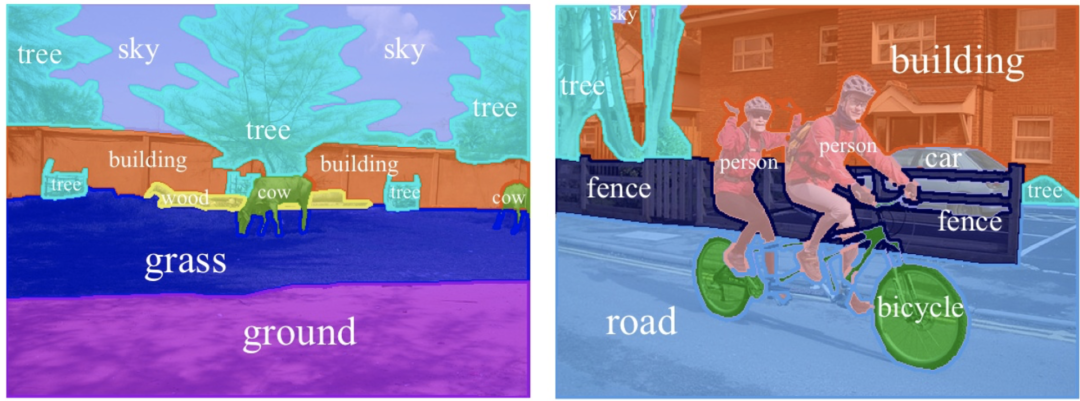
图分类

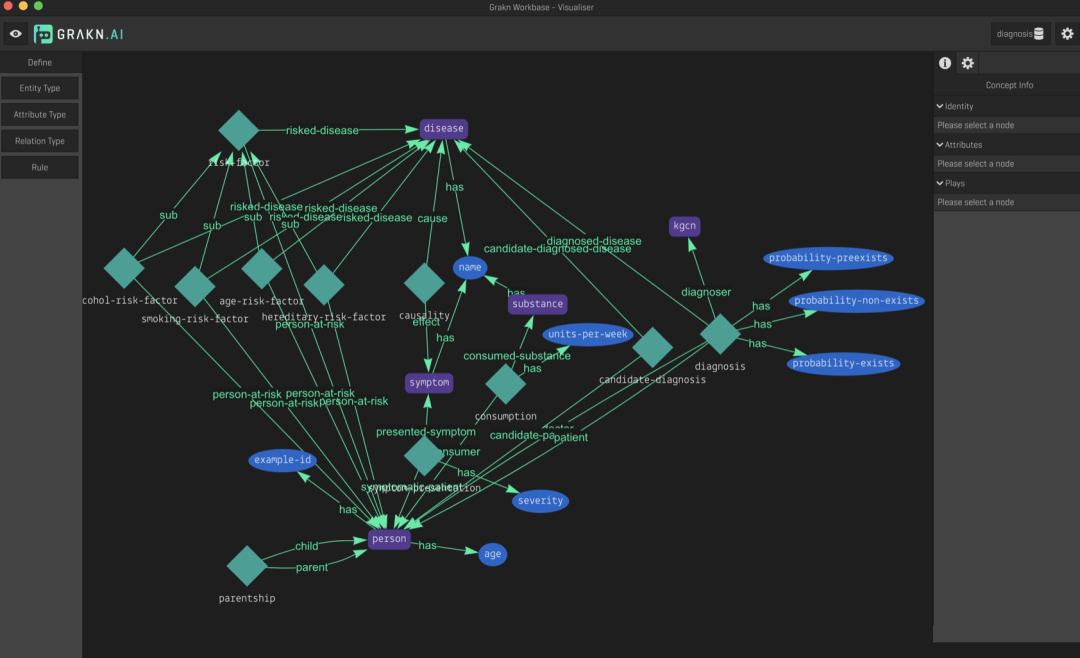
前沿的来了!GDL的现实应用


参考资料:
https://blog.paperspace.com/introduction-to-geometric-
deep-learning/
登录查看更多
相关内容
专知会员服务
115+阅读 · 2020年1月3日
Arxiv
13+阅读 · 2018年9月7日
Arxiv
10+阅读 · 2018年3月27日
Arxiv
4+阅读 · 2017年6月7日





